General Identification Condition for Causal Effects

0. Abstract

이 논문은 CE의 identifiability의 유용한 충분조건과 필요충분조건을 세운다.

1. Introduction

우리의 main task는 causal assumption의 CE가 identifiable한 지 결정하고 estimate하는 것이다.

Unmeasured confounder가 없다면 $P_t(y)$는 항상 identifiable하다.

만약 몇몇 confounder가 unmeasured라면 identifiability에 대한 질문이 발생하고 이는 confounder의 위치에 의존한다.

Identifiability에 대한 sufficient graphical condition은 Pearl의 챕터3&4에 정리되어 있다. 예를 들면,

• Valid adjustment set이 있을 경우, backdoor criterion이 있다.
• Valid adjustment set이 없는 경우, front-door criterion이 있다.

일반적인 $P_t(y)$에서 아래첨자를 없애려는 do-calculus로 이들을 유도할 수도 있다.

Do-calculus에 기반해서, Galles & Pearl 1995은 알고리즘을 제안하였다. 이 내용은 Pearl의 114~118에 나와있다.

---

이 논문은 현존하는 criteria를 간단하게 하고 일반화하는 새로운 identifiability condition을 제안한다.

• $P_x(v)$ is identifiable where $X$ is a singleton and $V$ is the set of all variables except $X$
• ${}^{\not \exists}$consecutive sequence of confounding arcs between $X$ & $Ch_X$

전체 변수인 $V$ 대신에 이의 subset인 $S$에 관심있는 경우에 대해선 충분조건을 제공한다.

• $P_x(s)$ is identifiable if ${}^{\not \exists}$consecutive sequence of confounding arcs between $X$ & $Ch_X$ in $G_{\text{An}(S)}$

2. Notation, Definitions, and Problem Formulation

2.1 Markovian causal model

$$P(v)=\prod_{i} P\left(v_{i} \mid p a_{i}\right) \quad \text{where } pa_i \text{ is the value of }Pa_i$$

모델은 $M=\left\langle V, G, P\left(v_{i} \mid p a_{i}\right)\right\rangle$들에 대한 명시를 하는 것이다.

Modularity assumption은 causal effect of $X$ on $V$를 예측할 수 있게 해준다.

$$P_{t}(v)=\left\{\begin{array}{ll} \prod_{\left\{i \mid V_{i} \notin T\right\}} P\left(v_{i} \mid p a_{i}\right) & v \text { consistent with } t \\ 0 & v \text { inconsistent with } t \end{array}\right.$$

이는 기존의 joint distribution에서 $T$에 대응하는 $P(v_i\mid pa_i)$를 1또는 0으로 바꾼 것이다.

$V$와 $G$는 assumption으로 둔 상황에서, $P(v_i \mid pa_i)$는 observational data로 estimate할 수 있으니 모든 CE는 identifiable하다.

2.2 semi-Markovian causal model

$$P(v)=\sum_{u} \prod_{i} P\left(v_{i} \mid p a_{i}, u^{i}\right) P(u) \quad \text{where } u^i \text{ is the unobserved parents of } V_i$$

모델은 $M=\left\langle V, U, G_{V U}, P\left(v_{i} \mid p a_{i}, u^{i}\right), P(u)\right\rangle$들에 대한 명시를 하는 것이다.

Factorization에서 unobserved variable $U$가 observed variable $V$의 descendent인 경우는 없다고 암묵적으로 가정한다.

$$P_{t}(v) =\left\{\begin{array}{ll} \sum_{u} \prod_{\left\{i \mid V_{i} \notin T\right\}} P\left(v_{i} \mid p a_{i}, u^{i}\right) P(u) & v \text { consistent with } t \\ 0 & v \text { inconsistent with } t \end{array}\right.$$

자연스럽게 $P_t(v)$를 observational distribution $P(v)$로 표현할 수 있을까라는 질문이 발생한다.

즉 Equation $(4)$에서 $u$가 들어간 $P(u)$텀과 $P\left(v_{i} \mid p a_{i}, u^{i}\right)$텀을 없애고 $P(v)$만으로 interventional distribution이 정의가 될까?

Definition 1 (Causal-Effect Identifiability)

​ The causal effect of $T$ on $S$ is identifiable from $G$ if $P_t(s)$ can be computed uniquely from $P(v) > 0$

직감적으로 말하면 SCM의 세부사항에 상관없이 observational distribution으로 결정된다는 것이다.

3. The Identification of $P_x(v)$

Let $X$ be a singleton variable.

We are interested in the problem of identifying the causal effect of $X$ on $V’ = V \setminus \{X\}$

표기의 편의를 위해 $P_x(v)$로 나타내겠다.

3.1 The easiest case

Theorem 1

​ ${}^{\not \exists}$bidirected edge connected to $X$ $\quad \Rightarrow \quad $ $P_{x}(v)=P\left(v \mid x, p a_{x}\right) P\left(p a_{x}\right)$

(Proof)

$$\begin{aligned} P(v) &= \sum_{u} \prod_{i} P\left(v_{i} \mid p a_{i}, u^{i}\right) P(u) \\ &= P\left(x \mid p a_{x}\right) \sum_{u} \prod_{\left\{i \mid V_{i} \neq X\right\}} P\left(v_{i} \mid p a_{i}, u^{i}\right) P(u) \\ &=P\left(x \mid p a_{x}\right) P_{x}(v) \end{aligned}$$

Hence, $P_{x}(v)=P(v) / P\left(x \mid p a_{x}\right)=P\left(v \mid x, p a_{x}\right) P\left(p a_{x}\right) .$

3.2 A more interesting case

Theorem 2

​ ${}^{\not \exists}$bidirected edge connected to $Ch_X$ $\quad \Rightarrow \quad $ $P_{x}(v)=\left(\prod_{\left\{i \mid V_{i} \in C h_{x}\right\}} P\left(v_{i} \mid p a_{i}\right)\right) \sum_{x} \frac{P(v)}{\prod_{\left\{i \mid V_{i} \in C h_{x}\right\}} P\left(v_{i} \mid p a_{i}\right)}$

(Proof)

​ Let $S=V \backslash\left(C h_{x} \cup\{X\}\right)$ and $A=\prod_{\left\{i \mid V_{i} \in S\right\}} P\left(v_{i} \mid p a_{i}, u^{i}\right)$.

• Then,
  • $\begin{aligned}P_x(v) &= \sum_{u} \prod_{\left\{i \mid V_{i} \in V \setminus \{X\}\right\}} P\left(v_{i} \mid p a_{i}, u^{i}\right) P(u) \\&= \prod_{\left\{i \mid V_{i} \in C h_{x}\right\}} \Big( P(v_{i} \mid p a_{i}) \Big)\prod_{\{i \mid V_i \in Ch_X\} }\sum_{u} A \cdot P(u) \end{aligned}$
  • $\begin{aligned}\sum_{u} A \cdot P(u) &= \sum_{u} \left(\sum_{x}P\left(x \mid p a_{x}, u^{x}\right) \cdot A \right)\cdot P(u) \quad \because A\text{ does not depend on }x\\ &= \sum_{x} \left( \sum_{u} P\left(x \mid p a_{x}, u^{x}\right) \cdot A \cdot P(u)\right ) \\ &= \sum_{x} \left( \sum_{u} P\left(x \mid p a_{x}, u^{x}\right)\cdot \frac{\prod_{\left\{i \mid V_{i} \in C h_{x}\right\}} P\left(v_{i} \mid p a_{i}\right)}{\prod_{\left\{i \mid V_{i} \in C h_{x}\right\}} P\left(v_{i} \mid p a_{i}\right)} \cdot A \cdot P(u)\right ) \\ &=\sum_{x} \frac{P(v)}{\prod_{\left\{i \mid V_{i} \in C h_{x}\right\}} P\left(v_{i} \mid p a_{i}\right)} \end{aligned}$
• Hence, $P_{x}(v)=\left(\prod_{\left\{i \mid V_{i} \in C h_{x}\right\}} P\left(v_{i} \mid p a_{i}\right)\right) \sum_{x} \frac{P(v)}{\prod_{\left\{i \mid V_{i} \in C h_{x}\right\}} P\left(v_{i} \mid p a_{i}\right)}$

---

Thm2의 유용성은 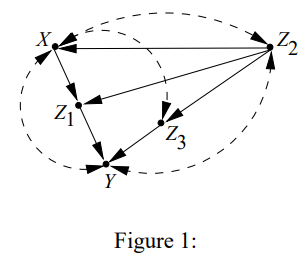이 상당히 복잡해보이나 간단하게 구할 수 있다.

$$\begin{aligned} P_{x}\left(z_{1}, z_{2}, z_{3}, y\right) &= P\left(z_{1} \mid x, z_{2}\right) \sum_{x^{\prime}} \frac{P\left(x^{\prime}, z_{1}, z_{2}, z_{3}, y\right)}{P\left(z_{1} \mid x^{\prime}, z_{2}\right)} \\ &= P\left(z_{1} \mid x, z_{2}\right) \sum_{x^{\prime}} P\left(y, z_{3} \mid x^{\prime}, z_{1}, z_{2}\right) P\left(x^{\prime}, z_{2}\right) \end{aligned}$$

3.3 The general case

Bidirected edge가 $X$에도 있고 $Ch_X$에 있어도 $P_x(v)$가 identifiable일 수 있다. 예를 들어, 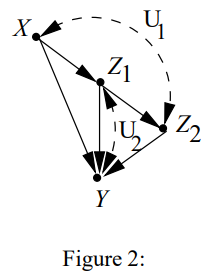의 경우,

$$\begin{aligned} P_{x}(v) &=\sum _{u_1, u_2} \prod _{\{i \mid V_i \neq X\}}p(v_i \mid pa_i, u^i) p(u_1)p(u_2) \\ &= \sum_{u_{1}} P\left(z_{2} \mid z_{1}, u_{1}\right) P\left(u_{1}\right) \cdot \sum_{u_{2}} P\left(z_{1} \mid x, u_{2}\right) P\left(y \mid x, z_{1}, z_{2}, u_{2}\right) P\left(u_{2}\right) \end{aligned}$$

Let

​ $Q_{1}=\sum_{u_{1}} P\left(x \mid u_{1}\right) P\left(z_{2} \mid z_{1}, u_{1}\right) P\left(u_{1}\right)$

​ $Q_{2}=\sum_{u_{2}} P\left(z_{1} \mid x, u_{2}\right) P\left(y \mid x, z_{1}, z_{2}, u_{2}\right) P\left(u_{2}\right)$.

Then,

​ $P(v) = Q_1 \cdot Q_2$

​ $P_x(v) = Q_2 \sum_{x’} Q_1$

그러므로, $Q_1$이나 $Q_2$가 identifiable하다면 그 나머지는 알아서 identifiable하고 $P_x(v)$도 identifiable하다.

• $Q_1$이 identifiable함을 보이겠다.
  • $\begin{aligned}P\left(x, z_{1}, z_{2}\right)&= \sum_y P(v) \\&= Q_1\cdot\sum_y Q_2\\&=Q_{1} \cdot \sum_{u_{2}} P\left(z_{1} \mid x, u_{2}\right) P\left(u_{2}\right) \\ &= Q_1 \cdot \sum_{u_{2}} P\left(z_{1} \mid x, u_{2}\right) P\left(u_{2}\mid x\right) \quad \because D-separation \\ &= Q_1 \cdot P(z_1\mid x)\end{aligned}$
• 그러므로,
  • $Q_1 = \frac{P\left(x, z_{1}, z_{2}\right)}{P(z_1 \mid x)} = P\left(z_{2} \mid x, z_{1}\right) P(x)$
  • $Q_{2}=P(v) / Q_{1}=P\left(y \mid x, z_{1}, z_{2}\right) P\left(z_{1} \mid x\right)$
  • $P_{x}(v)=P\left(y \mid x, z_{1}, z_{2}\right) P\left(z_{1} \mid x\right) \sum_{x^{\prime}} P\left(z_{2} \mid x^{\prime}, z_{1}\right) P\left(x^{\prime}\right)$

사실, bidirected edge가 $Ch_X$와 $X$에 있었으나 두 bidirected edge가 이어진 구조가 아니었다.

그렇기 때문에 $P(v)$가 $U_1$에 관한 $Q_1$텀과 $U_2$에 관한 $Q_2$텀이 서로 분리되었었다.

3.3.1 C-components

Bidirected path는 bidirected edge로만 이어진 path를 의미한다.

Bidirected path상의 노드들끼리 묶어서 graph의 component라고 하자.

$V = \{ S_1, \cdots, S_k\}$ component들의 부모인 unobserved variable들을 $U = \{ N_1, \cdots, N_k \}$로 표기하자.

$$Q_{j}:=\sum_{n_{j}} \prod_{\left\{i \mid V_{i} \in S_{j}\right\}} P\left(v_{i} \mid p a_{i}, u^{i}\right) P\left(n_{j}\right) \quad \text{for } j=1, \ldots, k$$

Then, $P(v)=\prod_{j=1}^{k} Q_{j} \quad \because \text{$N_{1}, \ldots, N_{k}$ are disjoint}$

---

각 $S_j$를 c-component of $G$라 부르고 $Q_j$를 c-factor corresponding to $S_j$라고 부르겠다.

예를들어, Figure 2에서 $S_{1}=\left\{X, Z_{2}\right\}$, $S_{2}=\left\{Z_{1}, Y\right\}$이다.

---

c-factor $Q_j$에 대한 두가지 해석

​ Let $P a(S)=S \cup\left(\cup_{V_{i} \in S} PA_{i}\right)$. Then,

• $Q_j$는 $Pa(S_j)$의 함수이다.
  • 왜냐면 $Pa(S_j)$의 값이 주어졌을 때 c-factor가 실수 값으로 결정되기 때문이다,
• $Q_j$는 $S_j$ 이외의 변수들을 intervention을 줬을 때의 분포이다.
  • 왜냐면 $Q_j = P_{v\setminus s_j}(s_j)$이기 때문이다.

---

Lemma 1

​ Let a topological order over $V$ be $V_1 < \cdots < V_n$.

​ Let $V^{(i)}=\left\{V_{1}, \ldots, V_{i}\right\}, \quad \text{for }i=1, \ldots, n$ and $V^{(0)}=\emptyset$,

​ For any $C \in V$, let $G_C$ denote the subgraph of $G$ composed only of $C$.

​ Then,

1. Each c-factor $Q_j$ is identifiable and is given by $Q_{j}=\prod_{\left\{i \mid V_{i} \in S_{j}\right\}} P\left(v_{i} \mid v^{(i-1)}\right)$
   1. Each factor $P\left(v_{i} \mid v^{(i-1)}\right) = P\left(v_{i} \mid p a\left(T_{i}\right) \backslash\left\{v_{i}\right\}\right) \quad $ where $T_i$ is the c-component of $G_{V^{(i)}}$ that contains $V_i$

(Proof) 수학적 귀납법

​ Base (n=1)

• $Q_1 = \sum_{u^1} p(v_1 \mid u^1)p(u^1)$ satisfies 1
• $P(v_1 \mid v^{(0)}) = P(v_1 \mid \emptyset)$ satisfies 2

​ Hypothesis (|V| = n인 상황)

• all $n$ c-factors are $Q_{j}=\prod_{\left\{i \mid V_{i} \in S_{j}\right\}} P\left(v_{i} \mid v^{(i-1)}\right)$
• all $V_i$ satisfies 2

​ Induction

• $|V|= n+1$인 상황에서

• Assume

  • $V$ is partitioned into c-components $S_{1}, \ldots, S_{l}, S^{\prime}$
  • 이 때, $S’$이 $V_{n+1}$이 속한 c-component라고 가정한다.

• Then, we have

  • $P(v)=Q^{\prime} \prod_{i} Q_{i}$
  • $P\left(v^{(n)}\right)= \sum_{v_{n+1}}P(v) = \left(\sum_{v_{n+1}} Q^{\prime}\right) \prod_{i} Q_{i} \quad \because \text{topological order & $Q_i$ is a function of $Pa(S_i)$}$

• Clearly, each $S_1 , \cdots, S_l$ is a c-component of $G_{V^{(n)}}$

  • Therefore, by the induction hypothesis, each $Q_i$ is identifiable and is given by

    $Q_j = \prod _{\{ i \mid V_i \in S_j\}} P(v_i \mid v^{(i-1)})$

  • Hence, $Q^{\prime}=\frac{P(v)}{\prod_{i} Q_{i}} = \frac{\prod _i P(v_i \mid v^{(i-1)})}{\prod _{\{ i \mid V_i \in S_j\}} P(v_i \mid v^{(i-1)})} = \prod_{\left\{i \mid V_{i} \in S^{\prime}\right\}} P\left(v_{i} \mid v^{(i-1)}\right)$

• WTS, $P(v_{n+1} \mid v^{(n)}) = P\left(v_{n+1} \mid p a\left(T_{n+1}\right) \backslash\left\{v_{n+1}\right\}\right)$

  • $T_{n+1}$은 $S’$이다.

  • $Q’= \prod_{\left\{i \mid V_{i} \in S^{\prime}\right\}} P\left(v_{i} \mid v^{(i-1)}\right)$은 $Pa(S’)$의 함수이다.

  • 이미 hypothesis에서 $V_{n+1}$빼고는 $P\left(v_{i} \mid v^{(i-1)}\right) = P\left(v_{i} \mid p a\left(T_{i}\right) \backslash\left\{v_{i}\right\}\right)$ 라고 가정하였다.

  • $Pa(T_i)$는 $Pa(S’)$의 부분집합이다.

  • 결국, $P(v_{n+1} \mid v^{(n)}) = \frac{Q’}{\prod_{\left\{i \mid V_{i} \in S^{\prime}\setminus \{V_{n+1}\}\right\}} P\left(v_{i} \mid v^{(i-1)}\right)}$ 역시 $Pa(S’)$의 함수이다.

  • 그렇기에, $P(v_{n+1} \mid v^{(n)}) $는 $C:= V \setminus Pa(S’)$에 독립인 함수이다.

  • $$\begin{array}{l} P\left(v_{n+1} \mid v^{(n)}\right)&=P\left(v_{n+1} \mid v^{(n)}\right) \sum_{c} P\left(c \mid p a\left(S^{\prime}\right) \backslash\left\{v_{n+1}\right\}\right) \quad \because \text{independence} \\&=\sum_{c} P\left(v_{n+1} \mid v^{(n)}\right) P\left(c \mid p a\left(S^{\prime}\right) \backslash\left\{v_{n+1}\right\}\right) \\ &=P\left(v_{n+1} \mid p a\left(S^{\prime}\right) \backslash\left\{v_{n+1}\right\}\right) \end{array}$$

---

Lemma 1을 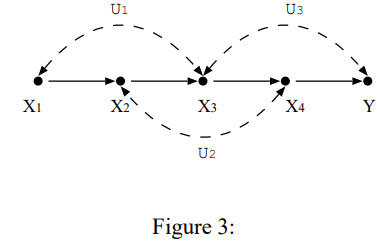에 적용하면 $S_{1}=\left\{X_{2}, X_{4}\right\}$과 $S_{2}=\left\{X_{1}, X_{3}, Y\right\}$에 대응하는 c-factor를 구할 수 있다.

$$\begin{aligned} Q_{1} &=\sum_{u_{2}} P\left(x_{2} \mid x_{1}, u_{2}\right) P\left(x_{4} \mid x_{3}, u_{2}\right) P\left(u_{2}\right) = P\left(x_{4} \mid x_{1}, x_{2}, x_{3}\right) P\left(x_{2} \mid x_{1}\right) \\ Q_{2} &=\sum_{u_{1}, u_{3}} P\left(x_{1} \mid u_{1}\right) P\left(x_{3} \mid x_{2}, u_{1}, u_{3}\right) P\left(y \mid x_{4}, u_{3}\right)= P\left(y \mid x_{1}, x_{2}, x_{3}, x_{4}\right) P\left(x_{3} \mid x_{1}, x_{2}\right) P\left(x_{1}\right) \end{aligned}$$

3.4 The identification criterion for $P_x(v)$

Let $X$ belong to the component $S^X$ with corresponding c-factor $Q^X$.

Let $Q_x^X$ denote the c-factor $Q^X$ with the term $P(x \mid pa_x , u^x)$ removed.

$$Q_{x}^{X}=\sum_{n^{X}} \prod_{\left\{i \mid V_{i} \neq X, V_{i} \in S^{X}\right\}} P\left(v_{i} \mid p a_{i}, u^{i}\right) P\left(n^{X}\right)$$

Then, we have $\begin{aligned}
P(v) &=Q^{X} \prod_{i} Q_{i} \\
P_{x}(v) &=Q_{x}^{X} \prod_{i} Q_{i}
\end{aligned}$

Since all $Q_i$ are identifiable by lemma 1, $P_x(v)$ is identifiable if and only if $Q_x^X$ is identifiable.

---

Theorem 3

​ $P_x(v)$ is identifiable if and only if ${}^{\not \exists}\text{Bidirected path between $X$ and $Ch_X$} $

​ When $P_x(v)$ is identifiable, it is given by $P_{x}(v)=\frac{P(v)}{Q^{X}} \sum_{x} Q^{X}$

(Proof)

(<==)

​ If ${}^{\not \exists}$BP btw $(X, Ch_X)$, then $Ch_X \cap S^X = \emptyset$

​ Therefore, in $Q^{X}=\sum_{n^{X}} \prod_{\left\{i \mid V_{i} \in S^{X}\right\}} P\left(v_{i} \mid p a_{i}, u^{i}\right) P\left(n^{X}\right)$, the only term $P(x \mid pa_x, u^X)$ has the $x$ variable.

​ So, we have $Q_{x}^{X}=\sum_{x} Q^{X}$.

​ Hence, $P_{x}(v) =Q_{x}^{X} \prod_{i} Q_{i}= \sum_{x} Q^{X}\prod_{i} Q_{i} =\left(\sum_{x} Q^{X}\right) \frac{P(v)}{Q^{X}} $

(==>)

​ ${}^{\exists}$BP btw $(X, Ch_X)$인 상황에서 $P(v)$는 같지만 $P_x(v)$가 다른 두개의 SCM을 찾아서 반례로 들면 된다.

---

Figure 3에 Thm 3을 적용해보자.

$$P_{x_{1}}\left(x_{2}, x_{3}, x_{4}, y\right)=Q_{1} \sum_{x_{1}'} Q_{2} = P\left(x_{4} \mid x_{1}, x_{2}, x_{3}\right) P\left(x_{2} \mid x_{1}\right) \sum_{x_1'} P\left(y \mid x_{1}, x_{2}, x_{3}, x_{4}\right) P\left(x_{3} \mid x_{1}', x_{2}\right) P\left(x_{1}'\right)$$

3.5 A Criterion for Identifying $P_{x}(s)$

Let $X$ be a singleton variable and $S \subset V$.

당연히, $P_x(v)$가 identifiable이면, $P_x(s)$도 identifiable하다.

하지만, 반대의 경우는 아니다.

Let $An(S) = S \cup \{ \text{ancestors of } S\}$ and $G_{An(S)}$ denote the subgraph of $G$ composed only $An(S)$

$An(S)$의 marmignal distribution은 주어진 SCM은 유지하되 $V \setminus An(S)$ 변수를 noise로 취급했을 때의 분포이다.

결론은 $P_x(s)$가 $G_{An(S)}$에서 identifiable하다는 것은 $P(an(S))$로 계산이 된다는 것이다.

여기에 Theorem 3을 적용하면, $G_(An(S))$에서 BP btw $(X, Ch_X)$가 없다면 identifiable하다는 것이다.

이는 강력한 충분조건에 해당한다.

---

이 criterion은 backdoor, frontdoor도 커버하면서 더 일반적인 기준이다.

4. Appendix

여기는 도저히 이해 못하겠다.

요즘 좀 추상적인 고민이 있는데 그래프에서의 모든 케이스에 대해서 대처하는 논법이 정말 어렵다는 생각을 한다.

과연 이 난관이 중요한 것인지 넘겨도 되는 것인지, 중요하다면 이 능력을 키우기에 적합한 방법이 있을 지 선천적인 건지…?

물론 어쩌면 다음주에 다시 왔을 때 한번에 이해할 수도 있을 수 있다.

일단 다음 논문인 Shpitser& Pearl 2006를 읽어보자.