이전 장에선, (policy search, policy iteration, value iteration)으로 policy evaluation과 control을 하였다.
이들은 암묵적으로 모델(reward probability& transition probability)에 대하여 안다고 가정하였다.
하지만 environment에 대한 model(dynamics)을 모르는 경우, model-free algorithm이 필요하다.
이번 장에선 policy evaluation만 다루겠다.
4.2 Dynamic Programming(Iterative algorithm)
이전 장에서, infinite horizon MDP에 대해서 iterative algorithm을 적용하였다.

DP라고 부르는 이유는 $V_k$에 대한 점화식으로 볼 수 있기 때문이다.
이를 backup diagram으로 표현할 수 있다.
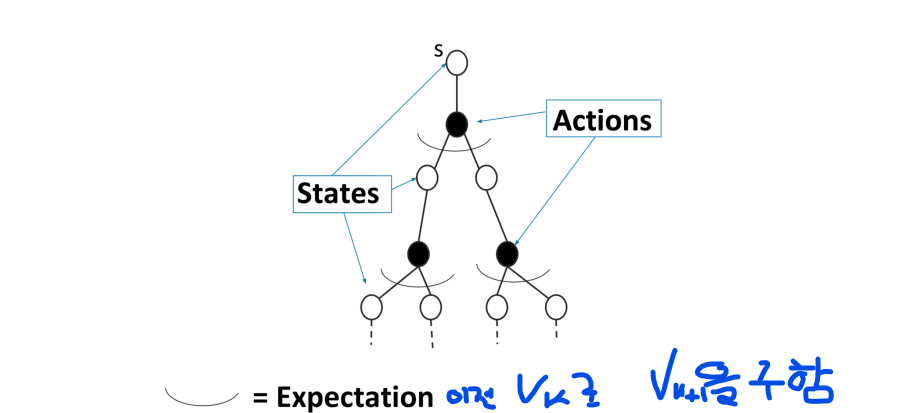
4.3 Monte Carlo On Policy Evaluation
이는 finite horizon을 갖는 episodic environment에서 작동한다.
Policy $\pi$로 episode를 생성하고 return 들을 기록하고 평균을 내는 방식이다.
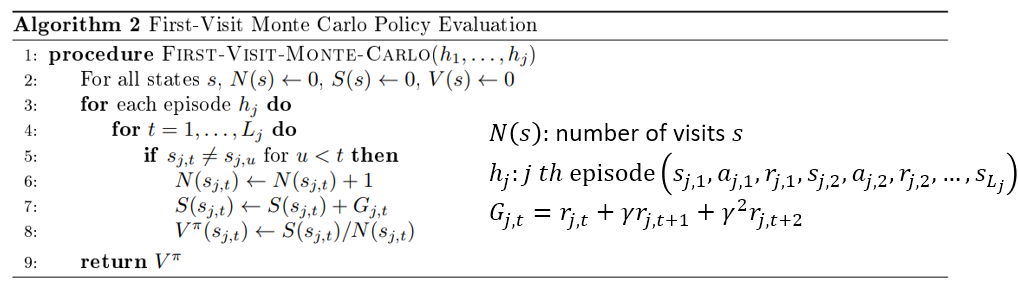
이를 backup diagram으로 표현하면 terminal state에서 끝나는 하나의 경로를 갖고서 업데이트를 하게 된다.
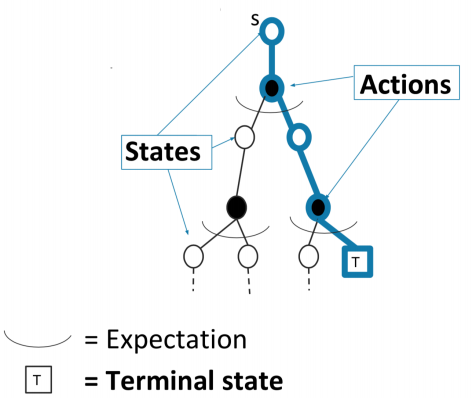
알고리즘의 line 8을 재표현하면 기존의 것에서 벗어난 정도에 의 가중치를 두고 업데이트하는 것으로 해석할 수 있다.
$\frac{1}{N}$을 $\alpha$로 일반적으로 표현한 것을 Incremental Monte Carlo On-Policy Evaluation이라고 한다.
4.4 Monte Carlo On-Policy Evaluation
On-policy는 evaluate하고 싶은 policy로 episode를 만들 수 있는 경우에 작동한다.
하지만, 비용적인 문제로 policy를 바꾸지 못하는 상황에서 다른 policy의 evaluation을 하고 싶다면?
즉, behavior policy(데이터 생성)와 target policy(값을 재고 싶은)가 다르다면?
4.4.1 Importance Sampling
Target distribution이 $q$이고 behavior distribution이 $p$인 상황에서 $\mathbb E_q [f(x)]$를 estimate하고 싶다.
즉, $p$ sampling으로 $\mathbb{E}_{x \sim q}[f(x)]$를 구할 수 있다.
4.4.2 Importance Sampling for On-Policy Evaluation
$\pi_1$:= target policy
$\pi_2$:= behavior policy
$V^{\pi_1}(s)$는 $\pi_2$ sampling으로 estimate가능하다.
4.5 Temporal Diffreence Learning
지금까지 DP(bootstrap)와 MC(sampling)으로 policy evaluation을 하였다.
Incremental MCPE에서, 기존의 것에서 벗어난 만큼에 가중치를 주고 업데이트하였다.
$G_t$를 전체 history의 realization으로 생각하지말고 $(s_t, a_t, r_t, s_{t+1})$까지만 realization으로 받고 나머진 marginalization하면,
로 바뀌게 된다. 이 때 $\delta_{t}=r_{t}+\gamma V^{\pi}\left(s_{t+1}\right)-V^{\pi}\left(s_{t}\right)$를 TD error라고 부른다.
Sampled reward와 next state value의 bootstrap estimate의 합 $r_{t}+\gamma V^{\pi}\left(s_{t+1}\right)$은 TD target이라고 부른다.

이를 backup diagram으로 표현하면 다음과 같다.
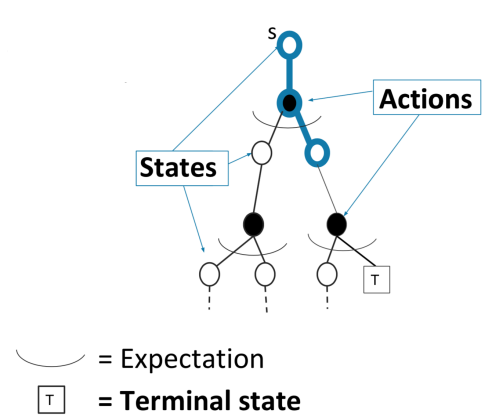
4.6 Summary of Methods Discussed
