4 Policy Gradients

가장 노테이션이 깔끔하다 생각된 버클리 CS294에 대한 요약이다.

목표 : optimal policy 함수의 parameter $\theta^{\star}=\arg \max _{\theta} E_{\tau \sim p_{\theta}(\tau)}\left[\sum_{t} r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right]$을 찾기

노테이션의 간편함을 위해 finite horizon $T$와 discount factor $\gamma=1$를 가정하겠다.

$\tau$는 $(s_1, a_1, \cdots, s_T, a_T, s_{T+1})$trajectory를 나타낸다.

1. Evaluation : Objective

$$J(\theta)=E_{\tau \sim p_{\theta}(\tau)}\left[\sum_{t} r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right] \approx \frac{1}{N} \sum_{i} \sum_{t} r\left(\mathbf{s}_{i, t}, \mathbf{a}_{i, t}\right)$$

2. Differentiation : Objective

$$\begin{aligned} \nabla_{\theta} J(\theta) &=\int \nabla_{\theta} \pi_{\theta}(\tau) r(\tau) d \tau \quad \quad \text{where } r(\tau) = \sum_{t=1}^T r(s_t, a_t) \\ &= \int \pi_{\theta}(\tau) \nabla_{\theta} \log \pi_{\theta}(\tau) r(\tau) d \tau \\ &= E_{\tau \sim \pi_{\theta}(\tau)}\left[\nabla_{\theta} \log \pi_{\theta}(\tau) r(\tau)\right] \\ &= E_{\tau \sim \pi_{\theta}(\tau)}\left[\left(\sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)\right)r(\tau)\right] \because \nabla_{\theta} \log p\left(\mathbf{s}_{t+1} \mid \mathbf{s}_{t}, \mathbf{a}_{t}\right) = 0 \\ & \approx \frac{1}{N} \sum_{i=1}^{N}\left(\sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i, t} \mid \mathbf{s}_{i, t}\right)\right)\left(\sum_{t=1}^{T} r\left(\mathbf{s}_{i, t}, \mathbf{a}_{i, t}\right)\right) \end{aligned}$$

이를 활용하여 policy gradient optimization을 하는 REINFORCE algorithm이 있다.

1. sample $\{ \tau^i \}$ from $\pi_{\theta} (\mathbf{a}_t \mid \mathbf s_t)$
2. $\nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N}\left(\sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i, t} \mid \mathbf{s}_{i, t}\right)\right)\left(\sum_{t=1}^{T} r\left(\mathbf{s}_{i, t}, \mathbf{a}_{i, t}\right)\right)$
3. $\theta \leftarrow \theta+\alpha \nabla_{\theta} J(\theta)$
4. repeat 1

3. Comparison to maximum likelihood

$$\begin{array}{l} \text { policy gradient: } \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N}\left(\sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i, t} \mid \mathbf{s}_{i, t}\right)\right)\left(\sum_{t=1}^{T} r\left(\mathbf{s}_{i, t}, \mathbf{a}_{i, t}\right)\right) \\ \text { maximum likelihood: } \nabla_{\theta} J_{\mathrm{ML}}(\theta) \approx \frac{1}{N} \sum_{i=1}^{N}\left(\sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i, t} \mid \mathbf{s}_{i, t}\right) \cdot 1\right) \end{array}$$

ML 파트는 supervised setting으로, action에 대한 label을 사람이 붙여준 것이다.

Reward가 양이면 likelihood를 높이고 음이면 likelihood를 낮추라고 gradient를 주게 된다.

Policy gradient를 trajectory term으로 표기하면

$$\begin{array}{l} \text { policy gradient: } \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \nabla_{\theta} \log \pi_{\theta}\left(\tau_{i}\right) r\left(\tau_{i}\right) \\ \text { maximum likelihood: } \nabla_{\theta} J_{\mathrm{ML}}(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \nabla_{\theta} \log \pi_{\theta}\left(\tau_{i}\right) \end{array}$$

좋은 trajectory는 나오게끔, 안좋은 trajectory는 안나오게끔 gradient를 주게 됨을 확인할 수 있다.

4. What is wrong with the policy gradient?

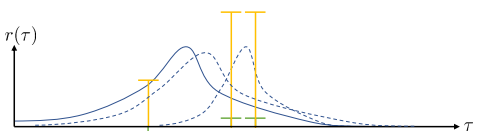
Density plot은 trajectory 상의 분포를 의미하며 점선은 policy gradient로 한번 update했을 때의 trajectory 상의 분포이다.

초록색 선은 original reward를 의미하며 노랑색 선은 reward 들에 constant를 더해준 것이다.

• Original updated distribution은 굉장히 좁은 형태의 density를 갖는다.

• Constant를 더해서 reward를 줬을 때의 distribution은 넓은 형태의 density를 갖는다.

Reward는 사람이 정의하기 나름인 함수라 굉장히 어색함을 느끼고 있을 것이다.

5. Reducing variance : Causality

$$\begin{aligned} \nabla_{\theta} J(\theta) &\approx \frac{1}{N} \sum_{i=1}^{N}\left(\sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i, t} \mid \mathbf{s}_{i, t}\right)\right)\left(\sum_{t=1}^{T} r\left(\mathbf{s}_{i, t}, \mathbf{a}_{i, t}\right)\right) \\ &\approx \frac{1}{N} \sum_{i=1}^{N}\left(\sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i, t} \mid \mathbf{s}_{i, t}\right) \sum_{t'=t}^{T} r\left(\mathbf{s}_{i, t'}, \mathbf{a}_{i, t'}\right)\right) \\ &=: \frac{1}{N} \sum_{i=1}^{N}\left(\sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i, t} \mid \mathbf{s}_{i, t}\right) \hat{Q}_{i, t}\right) \\ \end{aligned}$$

이는 $E_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{t+1} \mid \mathbf{s}_{t+1}\right) \times r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right] = 0$ 을 확인해보면 된다.

이를 관용적으로 causality라고 하는 지는 모르겠다.

6. Reducing variance : Baselines

$$\nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N}\left(\sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i, t} \mid \mathbf{s}_{i, t}\right)\right)\left(\sum_{t=1}^{T} r\left(\mathbf{s}_{i, t}, \mathbf{a}_{i, t}\right) -b\right)$$

where $b=\frac{1}{N} \sum_{i=1}^{N} r(\tau)$

단순하게 평균을 내는 방법은 간단하고 나쁘지 않은 baseline 선택지이다.

실제 optimal baseline이 tractable할 일은 없기 때문이다.

7. On-policy vs Off-policy learning

REINFORCE 기반의 알고리즘들은 모두 on-policy learning이고 sample efficiency가 떨어진다.

뽑은 trajectory들을 한번만 gradient update하고 버린다.

• $\pi_{\theta}(\tau)=p\left(\mathbf{s}_{1}\right) \prod_{t=1}^{T} \pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right) p\left(\mathbf{s}_{t+1} \mid \mathbf{s}_{t}, \mathbf{a}_{t}\right)$
• $\frac{\pi_{\theta}(\tau)}{\bar{\pi}(\tau)}=\frac{\prod_{t=1}^{T} \pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)}{\prod_{t=1}^{T} \bar{\pi}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)}$

Objective를 importance sampling form으로 표현하면

$$J\left(\theta^{\prime}\right)=E_{\tau \sim \pi_{\theta}(\tau)}\left[\frac{\pi_{\theta^{\prime}}(\tau)}{\pi_{\theta}(\tau)} r(\tau)\right]$$

이다. 이의 gradient는

$$\begin{aligned} \nabla_{\theta^{\prime}} J\left(\theta^{\prime}\right) &=E_{\tau \sim \pi_{\theta}(\tau)}\left[\frac{\nabla_{\theta^{\prime}} \pi_{\theta^{\prime}}(\tau)}{\pi_{\theta}(\tau)} r(\tau)\right] \\ &= E_{\tau \sim \pi_{\theta}(\tau)}\left[\frac{\pi_{\theta^{\prime}}(\tau)}{\pi_{\theta}(\tau)} \nabla_{\theta^{\prime}} \log \pi_{\theta^{\prime}}(\tau) r(\tau)\right] \\ &=E_{\tau \sim \pi_{\theta}(\tau)}\left[\left(\prod_{t=1}^{T} \frac{\pi_{\theta^{\prime}}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)}{\pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)}\right)\left(\sum_{t=1}^{T} \nabla_{\theta^{\prime}} \log \pi_{\theta^{\prime}}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)\right)\left(\sum_{t=1}^{T} r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right)\right] \\ &=E_{\tau \sim \pi_{\theta}(\tau)}\left[\sum_{t=1}^{T} \nabla_{\theta^{\prime}} \log \pi_{\theta^{\prime}}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)\left(\prod_{t^{\prime}=1}^{T} \frac{\pi_{\theta^{\prime}}\left(\mathbf{a}_{t^{\prime}} \mid \mathbf{s}_{t^{\prime}}\right)}{\pi_{\theta}\left(\mathbf{a}_{t^{\prime}} \mid \mathbf{s}_{t^{\prime}}\right)}\right)\left(\sum_{t^{\prime}=t}^{T} r\left(\mathbf{s}_{t^{\prime}}, \mathbf{a}_{t^{\prime}}\right)\right)\right] \\ &=E_{\tau \sim \pi_{\theta}(\tau)}\left[\sum_{t=1}^{T} \nabla_{\theta^{\prime}} \log \pi_{\theta^{\prime}}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)\left(\prod_{t^{\prime}=1}^{t} \frac{\pi_{\theta^{\prime}}\left(\mathbf{a}_{t^{\prime}} \mid \mathbf{s}_{t^{\prime}}\right)}{\pi_{\theta}\left(\mathbf{a}_{t^{\prime}} \mid \mathbf{s}_{t^{\prime}}\right)}\right)\left(\sum_{t^{\prime}=t}^{T} r\left(\mathbf{s}_{t^{\prime}}, \mathbf{a}_{t^{\prime}}\right)\right)\right] \end{aligned}$$

마지막에서 두번째 줄은 causality를 적용한 것이다.

마지막 줄은 아래의 식이 서로 같다는 것을 보이면 된다.

• $E_{\tau \sim \pi_{\theta}(\tau)}\left[\nabla_{\theta^{\prime}} \log \pi_{\theta^{\prime}}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)\left(\prod_{t^{\prime}=1}^{t+1} \frac{\pi_{\theta^{\prime}}\left(\mathbf{a}_{t^{\prime}} \mid \mathbf{s}_{t^{\prime}}\right)}{\pi_{\theta}\left(\mathbf{a}_{t^{\prime}} \mid \mathbf{s}_{t^{\prime}}\right)}\right)\right]$
• $E_{\tau \sim \pi_{\theta}(\tau)}\left[\nabla_{\theta^{\prime}} \log \pi_{\theta^{\prime}}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)\left(\prod_{t^{\prime}=1}^{t} \frac{\pi_{\theta^{\prime}}\left(\mathbf{a}_{t^{\prime}} \mid \mathbf{s}_{t^{\prime}}\right)}{\pi_{\theta}\left(\mathbf{a}_{t^{\prime}} \mid \mathbf{s}_{t^{\prime}}\right)}\right)\right]$

Causality에선 summation이라 $t \sim T$ term까지 살린 것이고

이번엔 product라 $1\sim t$까지 살린 것이다.