가장 노테이션이 깔끔하다 생각된 버클리 CS294에 대한 요약이다.
이번 장에선 이전 장의 policy gradient에 value function을 도입하고 actor-critic으로 이어나간다.
1. Improving the policy gradient
만약 reward to go $\hat Q_{i, t}$ 대신에 $Q\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)=\sum_{t^{\prime}=t}^{T} E_{\pi_{\theta}}\left[r\left(\mathbf{s}_{t^{\prime}}, \mathbf{a}_{t^{\prime}}\right) \mid \mathbf{s}_{t}, \mathbf{a}_{t}\right]$ 를 알 수 있다면 더 나은 estimator를 만들 수 있다.
추가로 $V\left(\mathbf{s}_{t}\right)=E_{\mathbf{a}_{t} \sim \pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)}\left[Q\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right]$ 를 알 수 있다면 좋은 baseline으로 채택할 수 있다.
이에 대한 직감적인 이유는 $A$는 state $s_t$를 기준으로 action $a_t$의 상대적 평가를 의미하는데 상대적 평가가 괜찮은 action에 대해선 likelihood를 높여주고 안좋은 action은 likelihood를 낮춰주기 때문이다.
2. Value function fitting
$A^{\pi}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)$ 를 구하기 위해, $V$와 $Q$를 둘 다 fitting하는 방식이 가장 먼저 떠오르겠지만
위의 관계식을 보면 $V$만 fitting해도 된다는 것을 알 수 있다.
Training data로 $\left\{\left(\mathbf{s}_{i, t}, \sum_{t^{\prime}=t}^{T} r\left(\mathbf{s}_{i, t^{\prime}}, \mathbf{a}_{i, t^{\prime}}\right)\right)\right\} = \left\{\left(\mathbf{s}_{i, t}, y_{i, t}\right)\right\}$ 를 사용해서 MSE Loss를 최적화하면 된다.
3. Lower variance : intro actor-critic
- Ideal target $y_{i, t}=\sum_{t^{\prime}=t}^{T} E_{\pi_{\theta}}\left[r\left(\mathbf{s}_{t^{\prime}}, \mathbf{a}_{t^{\prime}}\right) \mid \mathbf{s}_{i, t}\right]$
- Monte Carlo target $y_{i, t}=\sum_{t^{\prime}=t}^{T} r\left(\mathbf{s}_{i, t^{\prime}}, \mathbf{a}_{i, t^{\prime}}\right)$
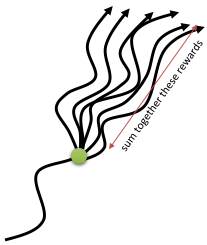
그러나 $\operatorname{Var}(r(s_{t+k}, a_{t+k}) \mid s_t)$가 $k$에 따라 커지므로 target value 자체의 분산이 큰 편이다.
$\sum_{t^{\prime}=t}^{T} E_{\pi_{\theta}}\left[r\left(\mathbf{s}_{t^{\prime}}, \mathbf{a}_{t^{\prime}}\right) \mid \mathbf{s}_{i, t}\right] \approx r\left(\mathbf{s}_{i, t}, \mathbf{a}_{i, t}\right)+V^{\pi}\left(\mathbf{s}_{i, t+1}\right)$ 라는 관계식을 이용해 bootstraped estimate를 target variable로 사용하여 value function fitting을 하자.
- $y_{i, t} \approx r\left(\mathbf{s}_{i, t}, \mathbf{a}_{i, t}\right)+\hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i, t+1}\right)$
4. Actor-critic algorithm (batch)
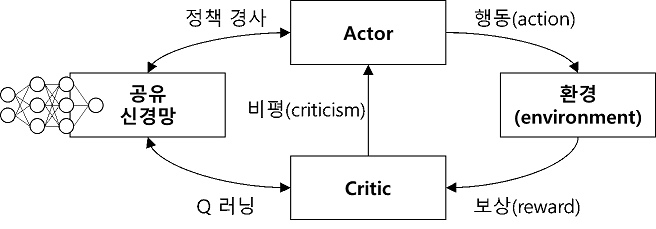
- Sample an episode $\left\{\mathbf{s}_{i}, \mathbf{a}_{i}\right\} \sim \pi_{\theta}(\mathbf{a} \mid \mathbf{s})$
- Fit $\mathcal{L}(\phi)=\left|\hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i}\right)-y_{i}\right|^{2} \quad $ where $y_{i, t} \approx r\left(\mathbf{s}_{i, t}, \mathbf{a}_{i, t}\right)+\hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i, t+1}\right)$
- Evaluate $\hat{A^{\pi}}\left(\mathbf{s}_{i}, \mathbf{a}_{i}\right)=r\left(\mathbf{s}_{i}, \mathbf{a}_{i}\right)+\hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i}^{\prime}\right)-\hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i}\right)$
- Estimate gradient estimator $\nabla_{\theta} J(\theta) \approx \sum_{i} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i} \mid \mathbf{s}_{i}\right) \hat{A}^{\pi}\left(\mathbf{s}_{i}, \mathbf{a}_{i}\right)$
- $\theta \leftarrow \theta+\alpha \nabla_{\theta} J(\theta)$
- Repeat 1.
5. Discount factors
Policy gradient 부터 지금까지 $\gamma = 1$을 가정하였었다.
우선 $J(\theta)=E_{\tau \sim p_{\theta}(\tau)}\left[\sum_{t=1} \gamma^{t-1} r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right]$ 로 뒀을 때의 unbiased estimator들을 소개하겠다.
- $\nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N}\left(\sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i, t} \mid \mathbf{s}_{i, t}\right)\right)\left(\sum_{t=1}^{T} \gamma^{t-1} r\left(\mathbf{s}_{i, t^{\prime}}, \mathbf{a}_{i, t^{\prime}}\right)\right)$
- $\begin{aligned}\nabla_{\theta} J(\theta) &\approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i, t} \mid \mathbf{s}_{i, t}\right)\left(\sum_{t^{\prime}=t}^{T} \gamma^{t^{\prime}}\left(\mathbf{s}_{i, t^{\prime}}, \mathbf{a}_{i, t^{\prime}}\right)\right) \\ &= \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} \gamma^{t-1} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i, t} \mid \mathbf{s}_{i, t}\right)\left(\sum_{t^{\prime}=t}^{T} \gamma^{t^{\prime}-t} r\left(\mathbf{s}_{i, t^{\prime}}, \mathbf{a}_{i, t^{\prime}}\right)\right)\end{aligned}$
그러나 실제로 주로 사용하는 건 아래의 biased estimator이다.
- $\nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i, t} \mid \mathbf{s}_{i, t}\right)\left(\sum_{t^{\prime}=t}^{T} \gamma^{t^{\prime}-t} r\left(\mathbf{s}_{i, t^{\prime}}, \mathbf{a}_{i, t^{\prime}}\right)\right)$
이는 마지막에 소개한 unbiased estimator와 굉장히 유사하나 시간이 지날수록 learning signal을 줄이는 꼴이 아니다.
이는 reasonable하다고 볼 수 있는 form이라 자주 사용된다.
직감적으로 말하면 이전의 기록을 현재 policy update에 반영하고 싶지 않은 마음이다
6. Actor-critic algorithm w/ discount (batch & online)
Batch version
- Sample an episode $\left\{\mathbf{s}_{i}, \mathbf{a}_{i}\right\} \sim \pi_{\theta}(\mathbf{a} \mid \mathbf{s})$
- Fit $\mathcal{L}(\phi)=\left|\hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i}\right)-y_{i}\right|^{2} \quad $ where $y_{i, t} \approx r\left(\mathbf{s}_{i, t}, \mathbf{a}_{i, t}\right)+ \gamma \hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i, t+1}\right)$
- Evaluate $\hat{A^{\pi}}\left(\mathbf{s}_{i}, \mathbf{a}_{i}\right)=r\left(\mathbf{s}_{i}, \mathbf{a}_{i}\right)+\gamma \hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i}^{\prime}\right)-\hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i}\right)$
- Estimate gradient estimator $\nabla_{\theta} J(\theta) \approx \sum_{i} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i} \mid \mathbf{s}_{i}\right) \hat{A}^{\pi}\left(\mathbf{s}_{i}, \mathbf{a}_{i}\right)$
- $\theta \leftarrow \theta+\alpha \nabla_{\theta} J(\theta)$
- Repeat 1.
Online version
- Given $\mathbf s_{i, t}$, sample 1-step $\left\{\mathbf{s}_{i,t+1}, \mathbf{a}_{i,t}\right\} \sim \pi_{\theta}(\mathbf{a} \mid \mathbf{s})$
- Fit $\mathcal{L}(\phi)=\left|\hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i,t}\right)-y_{i,t}\right|^{2} \quad $ where $y_{i, t} \approx r\left(\mathbf{s}_{i, t}, \mathbf{a}_{i, t}\right)+\gamma \hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i, t+1}\right)$
- Evaluate $\hat{A^{\pi}}\left(\mathbf{s}_{i, t}, \mathbf{a}_{i, t}\right)=r\left(\mathbf{s}_{i,t}, \mathbf{a}_{i,t}\right)+\gamma \hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i,t+1}\right)-\hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i,t}\right)$
- Estimate gradient estimator $\nabla_{\theta} J(\theta) \approx \sum_{i} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i,t} \mid \mathbf{s}_{i,t}\right) \hat{A}^{\pi}\left(\mathbf{s}_{i,t}, \mathbf{a}_{i,t}\right)$
- $\theta \leftarrow \theta+\alpha \nabla_{\theta} J(\theta)$
- Repeat 1.
비동기 버전의 online actor-critic도 있는데 스킵하겠다.
$TD(\lambda)$같이 다양한 n-step으로 구한 advantage function를 종합하는 것도 있는데 자세한 건 Generalized Advantage Estimation 논문 보기!