Study Repo
0%

Proximal-Policy-Optimization-Algorithms

Posted on Edited on In Disqus:

0. Abstract

Standard policy gradient method는 sample마다 한번의 gradient update를 하고 버린다.

PPO는

  1. minibatch를 갖고서 여러번의 update를 한다.
  2. TRPO의 일부 장점들을 가져온다.
  3. TRPO보다 더 간단하고 더 나은 sample-complexity를 갖는다.

1. Introduction

DQN은 discrete action space에만 적용이 된다.

Continuous action space의 경우 policy gradient method를 생각할 수 있다.

하지만 Vanilla policy rgadient method는 robustness와 data efficiency가 낮다.

Robustness는 hyperparameter tuning 없이 다른 문제들에 적용이 가능함을 말한다.

TRPO는 이 문제들을 해결했으나

  1. 너무 복잡하고
  2. architecture에 noise를 줄 수 없고 (dropout 불가능)
  3. value function과 policy간의 parameter 공유가 불가능하다.

PPO는 TRPO의 안정적 성능과 data efficiency를 챙기지만 일차미분만 활용하는 알고리즘이다.

Continuous control에선 다른 알고리즘을 압도하고 Atari에선 A2C보다 낫고 ACER와 비슷하다.

2. Background: Policy Optimization

2.1 Policy Gradient Methods

가장 흔히 사용되는 gradient estimator $\hat{g}=\hat{\mathbb{E}}_{t}\left[\nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right) \hat{A}_{t}\right]$

  • $\hat{\mathbb{E}}_{t}[\ldots]$ 은 $t$ 시점에서 finite batch of samples에 대한 empirical average
  • $\hat{A}_{t}$ 은 $t$ 시점에서 advantage function에 대한 estimator
  1. Sampling $\tau$
  2. Optimizing value function $\hat V$ and policy function $\pi$
  3. repeat 1.

2번의 Opimization 과정에서 gradient descent를 여러번 하는 건 objective function이 수식적으로 정의가 안된 최적화이고 종종 collapse된다.

2.2 Trust Region Methods

이는 objective function에 linear approximation을 하고 constraint에 quadratic approximation을 한 후에 conjugate gradient algorithm을 사용해서 근사적으로 풀 수 있다.

TRPO의 논문에서 이론적으로 제시했던 바는

였지만, penalty term 대신 constraint를 했던 이유는 $\beta$의 선택이 문제가 됐기 때문이다.

PPO는 추가적인 modification을 더해서 penalty term이 있는 꼴로 최적화할 것이다.

그 경우 일차미분으로 최적화가 가능해진다.

3. Clipped Surrogate Objective

미분을 했을 때 policy gradient가 나오는 대리 함수를 surrogate objective function이라 한다.

  • $L^{P G}(\theta)=\hat{\mathbb{E}}_{t}\left[\log \pi_{\theta}\left(a_{t} \mid s_{t}\right) \hat{A}_{t}\right]$ ; 이 때 $\hat {\mathbb E}_t$는 $\theta$로 뽑은 것의 empirical average
  • $L^{C P I}(\theta)=\hat{\mathbb{E}}_{t}\left[\frac{\pi_{\theta}\left(a_{t} \mid s_{t}\right)}{\pi_{\theta_{\text {old }}}\left(a_{t} \mid s_{t}\right)} \hat{A}_{t}\right]$ ; 이 때 $\hat {\mathbb E}_t$는 $\theta_{\text{old}}$로 뽑은 것의 empirical average

TRPO에서도 사용했던 두 번째 surrogate objective를 단순하게 gradient로 update하는 것은 확률의 ratio에 따라서 너무 큰 step을 갖게 된다.

어를 방지하기 위해, $r_t(\theta):= \frac{\pi_{\theta}\left(a_{t} \mid s_{t}\right)}{\pi_{\theta_{\mathrm{old}}}\left(a_{t} \mid s_{t}\right)}$ 이 $\hat{A}_{t}$을 너무 키우지 않게끔 penalize를 하는 objective를 제안한다.

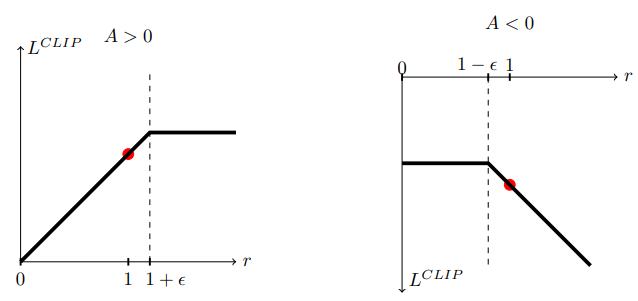
  • objective를 향상시키는 policy의 변화에서 $r$이 $1+\epsilon$ 보다 큰 경우 gradient signal을 버리게 된다.
  • objective를 하향시키는 policy의 변화에서 $r$이 $1-\epsilon$ 보다 작은 경우 gradient signal을 버리게 된다.

더 직감적으로 말하면, advantage의 향상을 가져오는 sample 중에서 큰 policy의 변화가 있다면 update에 사용하지 않는다.

Note that

  1. $L^{C L I P}(\theta)=L^{C P I}(\theta)$ if $\theta = \theta_{\text {old }}$
  2. $\nabla _{\theta}L^{C L I P}(\theta)= \nabla _{\theta}L^{C P I}(\theta)$ if $\theta \approx \theta_{\text {old }}$

4. Adaptive KL Penalty Coefficient

TRPO 논문에서 제안됐지만 penalty coefficient의 적절함이 없어서 못 쓴

를 휴리스틱하게 KL divergence가 크면 $\beta$를 늘려주고 작으면 $\beta$를 줄여주는 방법도 있다.

5. Algorithm

Asynchronous methods for deep reinforcement learning

​ 은 (T-t) step TD error를 advantage function estimator로 쓴 것이다.

High-Dimensional Continuous Control Using Generalized Advantage Estimation

​ 은 1~(T-t) step TD error의 exponential average를 advantage function estimator로 쓴 것이다.

Value function 학습엔 MSELoss를 사용한다.

추가로 sufficient exploration을 보장하기 위해 entropy bonus를 더하자.