0. Abstract
CE estimation에 관심이 있다.
- CE of $\mathbf X \subset \mathbf V$ on $\mathbf Y \subset \mathbf{V \setminus X}$ 이 identifiable 한 지에 대한 그래프적 필요충분조건
- Identifiable할 때 이를 구하는 algorithm
- 이게 연속적 do-calculus의 적용임을 보이겠다.
- Tian & Pearl 2002은 이의 특수 케이스임을 보이겠다.
- 모든 CE가 identifiable한 semi-Markovian model들에 대한 characterization을 제공한다.
1. Introduction
Markovian Causal Model에 대한 all CEs are identifiable의 논의는 Pearl 책에 나와있다.
만약 causal graph에 hidden common cause에 해당하는 bidirected arc가 존재하는 경우 Semi Markovian Causal Model이라고 한다.
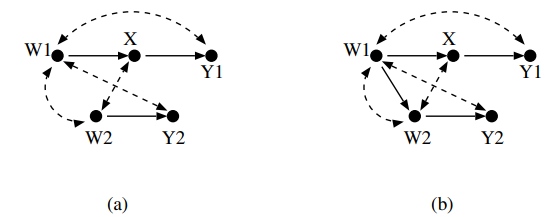
(a)는 identifiable하고 (b)는 not identifiable하다.
최근 Tian & Pearl 2002은 $(X, Ch_X)$ 사이에 bidirected path가 없음이 $P_x(v)$의 identifiable에 필요충분조건임을 증명했다.
이 때 $X$는 singleton variable이고 $V = \mathbf{V \setminus} X$로 제한되었다.
- 이 논문에선 좀 더 일반적으로 CE of $\mathbf X \subset \mathbf V$ on $\mathbf Y \subset \mathbf{V \setminus X}$ 이 identifiable 한 지에 대한 그래프적 필요충분조건
- Identifiable할 때 이를 구하는 algorithm을 도출하고
- Algorithm이 연속적 do-calculus의 적용임을 보이겠다.
- Tian & Pearl 2002과의 비교
- 모든 CE가 identifiable한 semi-Markovian model들에 대한 characterization을 제공한다.
2. Notation and Definitions
- 대문자 : random variable
- 소문자 : random variable의 sampled value
- Bold 문자 : set of variables
- Root set : $\left\{X \in G \mid D e(X)_{G}=\emptyset\right\}$
- Probabilistic causal model $M=\langle\mathbf{U}, \mathbf{V}, \mathbf{F}, P(\mathbf{U})\rangle$
- $\mathbf V$ is a set of observable variables
- $\mathbf U$ is a set of unobservable variables that follows $P(\mathbf{U})=\prod_{i} P\left(U_{i}\right)$
- $\mathbf F = \{ f_V\}_{V\in \mathbf V}$ ia a set of functions
- Each variable $V \in \mathbf V$ has a corresponding function $f_V \in \mathbf F$ that determines the value of $V$
- $G$ : induced graph by $M$
- 여기서 bidirected edge between $(X, Y)$는 $f_X$와 $f_Y$가 같은 $U \in \mathbf U$를 input으로 공유함을 의미한다.
- $P(\mathbf V)$ : induced distribution by $\mathbf F , P(\mathbf U)$
- 다른 논문들에선 터프하게 $P(\mathbf V)$에 positive distribution을 가정하였지만
- 우리 논문에선 고려하는 $P(\mathbf{W} \mid \mathbf{Z})$들에 대해서만, $P(\mathbf{Z})$에 positive distribution을 가정한다.
- Intervention $do(\mathbf x)$에서 $P\left(\mathbf{x} \mid P a(\mathbf{X})_{G} \setminus \mathbf{X}\right)>0$ 이 만족되지 않으면 $P_\mathbf x(\mathbf V)$는 정의되지 않는다.
인 경우, $P$ is markovian with respect to $G$이며, $P$는 D-separation을 따른다.
Intervention $do(\mathbf x)$은 새로운 SCM $M_{\mathbf{x}}=\left\langle\mathbf{U}, \mathbf{V}, \mathbf{F}_{\mathbf{x}}, P(\mathbf{U})\right\rangle$을 만든다.
이 때, $\mathbf{F}_{\mathbf{x}}$는 $f_{\mathbf X} = \mathbf x$로 고정함을 의미한다.
Lemma 1
Let $\mathbf {X} , \mathbf{Y}$ be tow sets of variables.
Assume ${}^{\exists}M^1 \& M^2$ s.t.
- have same induced graph $G$
- have same induced distribution $P^{1}(\boldsymbol{V})=P^{2}(\boldsymbol{V}) =: P(\mathbf V)$
- have different intervention distributions $P_{x}^{1}(\boldsymbol{Y}) \neq P_{\boldsymbol{x}}^{2}(\boldsymbol{Y})$ for some $\mathbf x : \quad P\left(\boldsymbol{x} \mid P a(\boldsymbol{X})_{G} \backslash \boldsymbol{X}\right)>0$
Then, $P_{\boldsymbol{x}}(\boldsymbol{y})$ is not identifiable in $G$
직감적으로 말하면, observation distribution만이 $P_{\mathbf x}(\mathbf y)$를 결정하는 게 아니라, SCM의 세부적인 정의가 관여한다면 identifiable하지 않다.
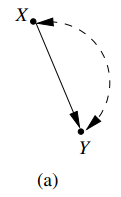
이 제일 간단한 예시로 induced distribution은 같지만 intervention distribution이 다른 두 SCM $M^1$, $M^2$를 세워서 not identifiable임을 보이자.
- $U \sim \text{Ber}(0.5)$
- $f_X(u) = u$
- $f^1_Y(x, u) = \text{XOR}(u, x) \quad , \quad f^2_Y(x, u) = 0$
- Then, $P^1(X, Y) = P^2(X, Y)$
- However, $P^1_x(Y=0) = 0.5 \neq P^2_x(Y=0) = 1$
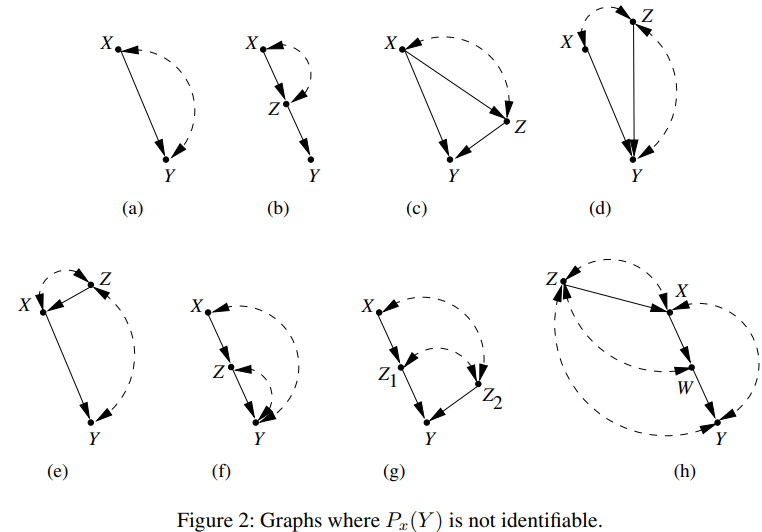
은 Pearl이 제시한 identifiable하지 않은 그래프들의 예시이다.
3. C-Trees and Direct Effects
C-component는 bidirected edge로 연결된 node들의 그룹이다.
Tian & Pearl 2002, Tian 2002이 말하길
- ${}^{\forall}\mathbf{C} \subset G$, the quantity $P_{\mathbf{v} \backslash \mathbf{c}}(\mathbf{C})$ is identifiable.
- $P(\mathbf{V}) = \prod_{\mathbf C} Q(\mathbf C) \quad \text{where c-factor } Q(\mathbf C) = P_{\mathbf{v} \backslash \mathbf{c}}(\mathbf{C})$
- C-factor를 이용한 factorization은 identification problem을 소문제들로 분해해주기 떄문에 굉장히 유용하다.
Semi-Markovian Model에서 정의된 C-component의 그래프 버전으로 C-tree를 도입한다.
Definition 4
Let $G$ be a semi-Markovian graph s.t.
- $G$ is a C-component
- Each node $V$ has at max one child
- $\{Y\} \cup An(Y)_G = G$
Then $G$ is a $Y$-rooted C-tree.
$G$에 $Y$-rooted C-tree인 subgraph가 없다면, directed effect on $Y$는 identifiable하다.
Directed effect on $Y$가 $P_{p a(Y)}(Y)$와 거의 동치인게 잘 받아들여지지 않을 거라 예상한다.
자세한 내용은 Pearl의 4장을 보길 바란다.
Lemma 2
Let $M$ be a causal model with graph $G$.
Then, ${}^\forall Y \in \mathbf V, $ $P_{p a(Y)}(Y)$ is identifiable if ${}^{\not \exists} Y\text{-rooted C-tree subgraph in } G$
(Proof)
- Tian 2002, Thm 21에서 $Y$를 포함하는 C-component에 $Y$의 부모가 없다면
- $P_{p a(Y)}(Y)$가 identifiable함을 보였다.
- $Y$-rooted C-tree가 하나도 없다는 것은 C-component에 $Y$의 부모, 조상이 없다는 것을 의미한다.
Theorem 3
Let $G$ be a $Y$-rooted C-tree.
Then effect of any $\mathbf X \subset G \setminus\{Y\}$ on $Y$ is not identifiable.
(Proof)
- $M^1$: $V_k := \text{sum} (pa_{V_k}) \text{ mod } 2$
- $M^2$: $V_k := \text{sum} (pa_{X_k}) \text{ mod } 2$ ; 대신에 $Y=0$
- $U = \text{Ber}(0.5)$
- $G$가 $Y$-rooted C-tree이기 때문에 $U$는 2개의 자식을 갖고 $Y$로 가는 방향을 갖는다.
- 결국, $P^1(Y=1) = P^2(Y=1) = 0$이다.
- $\begin{aligned}
{}^{\forall} \mathbf X \subset G\setminus\{Y\}, \quad {}^{\exists}U \text{ s.t.} & \text{ one of child is in }An(\mathbf X)_G \text{ and }\\& \text{ one of child is not in }An(\mathbf X)_G
\end{aligned}$ - 결국, $P^2_{\mathbf x}(Y=1) =0 \neq P^1_{\mathbf x} (Y=1) >0$
Corollary 1
Let $G$ be a semi-Markovian graph.
Let $\mathbf X$ and $\mathbf Y$ be disjoint sets of variables.
If ${}^{\exists} W \in An(Y)_{\underline {\mathbf X} }$ s.t. $W$-rooted C-tree in $G$ which contains any $X \in \mathbf X$,
then $P_{\mathbf x}(\mathbf Y)$ is not identifiable.
(Proof)
- Let $T$ be a $W$-rooted C-tree
- Let $p$ a path $W\rightarrow Y \in \mathbf Y$
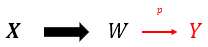
- In the graph $p \cup T$, $P_{\mathbf{x}}(Y)=\sum_{w} P_{\mathbf{x}}(w) P(Y \mid w)$
- 즉, $P>0$인 경우 $P_{\mathbf{x}}(Y)$의 identifiable과 $P_{\mathbf{x}}(w)$의 identifiable은 동치이다.
- Theorem 3에 의해 $P_{\mathbf{x}}(W)$이 not identifiable in $T$임을 알 수 있다.
- 결국 $P_{\mathbf{x}}(Y)$이 not identifiable in $p \cup T$이다.
- 이게 $P_{\mathbf{x}}(Y)$이 not identifiable in $G$로 확장이 되는 이유는 뭘까????
비록 $Y$-rooted C-tree가 없더라도, $Y$의 ancestor set이 not identifiable이라면 $P_{\mathbf x}(Y)$가 not identifiable일 수 있다…?
4. C-Forests, Hedges, and Non-Identifiability
Corollary 1에서 effect on single variable $Y$의 identifiability에 필요조건을 만들었다.
이번 섹션에선 C-tree의 multi-root로의 확장인 C-forest를 도입하여 effect on $\mathbf Y$에 대해 논의하겠다.
Definition 5 (C-forest)
Let $G$ be a semi-Markovian graph, where $\mathbf Y$ is the root set.
Then $G$ is a $\mathbf Y$-rooted C-forest if
- $G$ is C-component
- all obersavable nodes $V$ have at most one child
3장에서 C-tree와 direct effect간의 관계가 있었던 것 처럼
이번 장에서 C-forests와 general effects $P{\mathbf x}(\mathbf Y)$와의 관계가 있음을 보이겠다.
이를 위해 C-forest의 쌍으로 구성된 structure인 hedge를 도입하겠다.
Definition 6 (hedge)
Let $\mathbf X, \mathbf Y$ be disjoint sets of variables in $G$.
Let $F, F’$ be $\mathbf R$-rooted C-forests s.t. $\left\{\begin{array}{l} F \cap \mathbf{X} \neq \emptyset \\ F^{\prime} \cap \mathbf{X}=\emptyset \\ F^{\prime} \subset F \\ \mathbf{R} \subset A n(\mathbf{Y})_{\overline{\mathbf{X}}} \end{array}\right.$
Then $F \& F’$ forms a hedge for $P_{\mathbf x}(\mathbf y)$ in $G$.
hedge 예시
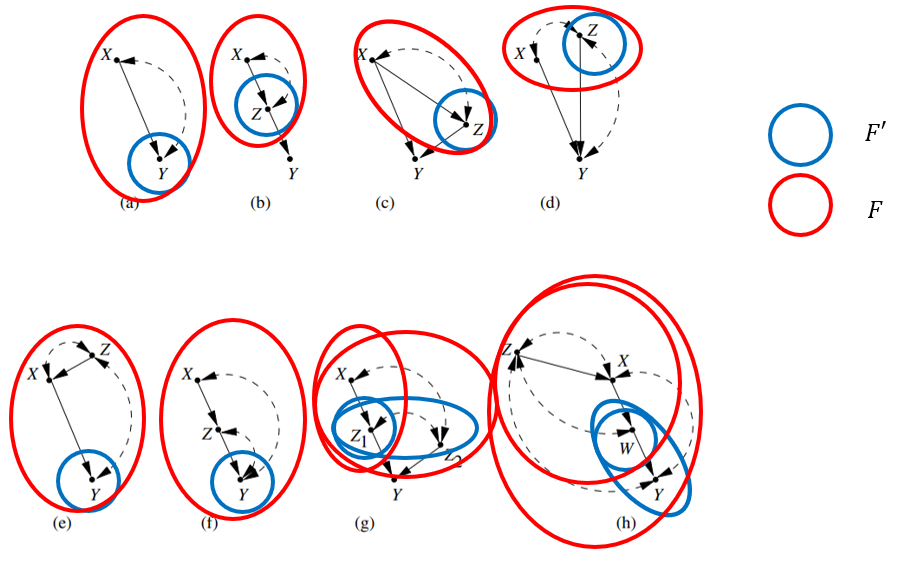
hedge 형성이 안 되는 예시
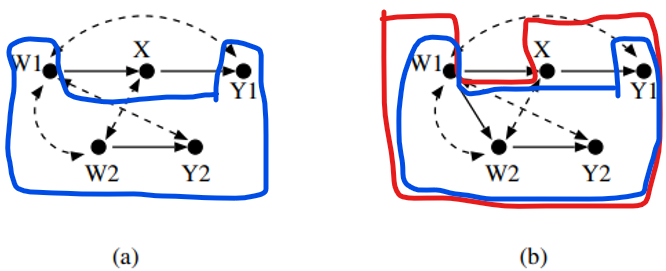
(a)는 hedge를 형성하지 못하고 (b)는 hedge를 형성한다.
(a)에서 $W_1$을 Root set에 포함하지 않으면 $Y_1, Y_2$를 동시에 포함하는 C-forest를 형성할 수 없다.
하지만 $W_1$은 $A n(\mathbf{Y})_{\overline{\mathbf{X}}}$에 포함되지 않는다.
Theorem 4
Assume ${}^{\exists} \mathbf R$-rooted C-forests $F, F’$ that form a hedge for $P_{\mathbf x}(\mathbf y)$ in $G$.
Then $P_{\mathbf x}(\mathbf y)$ is not identifiable in $G$.
증명이 어려워서 스킵하겠다…
semi Markovian causal model에서의 identifiability의 필요충분조건을 정복하고 싶었으나 어려워서 일단 미뤄야겠다. ㅠ
패배감에 너무 상심이 크다
비슷한 주제지만 가독성이 좋아보이는 Huang & Valtorta 2006으로 곧 리트라이 해보겠다!