0. Abstract
VAE에 영감을 받아서 latent variable을 RNN hidden state의 input으로 포함한다.
VRNN은 highly structured sequential data에서 관측되는 variability를 모델링할 수 있다.
그렇기에 latent variable이 RNN dynamics에서 굉장히 중요한 역할을 한다.
1. Introduction
Dynamic Bayesian Network라는 분야에서 가장 대표적인 모델
- Hidden Markov models
- Kalman filters
DBN과 RNN의 공통점
- transition function $f: h_t \rightarrow h_{t+1}$
- mapping $g$ : $h_t \rightarrow x_t$
DBN과 RNN의 차이점
- DBN의 transition function은 굉장히 간단한 함수를 사용하지만 RNN은 뉴럴넷을 사용한다.
- DBN의 hidden state는 표현력이 약한 hidden state를 사용하나 RNN은 고차원 hidden state를 사용한다.
전반적으로 DBN은 제약이 많이 걸린 모델이라 highly structured sequential data의 generative model로 RNN이 훨씬 선호된다.
DBN에서의 hidden state는 latent random variable이지만 RNN의 hidden state는 deterministic value이다.
결국 RNN은 다양한 시간 차 별로 complex dependency를 갖는 구조에서 부적절한 모델링 방식일 수 있다.
[2, 4]에서 complex dependency가 unimodal (혹은 mixture of unimodal로 하더라도) standard RNN으론 모델링 될 수 없다고 이야기 했다.
이 말의 정확한 의미는 모르겠으나 standard RNN은 태생적으로 분포의 다양성을 인정하지 못함을 말하는 것 같다.
이 논문은 high dimensional sequential data에 대해서, VRNN을 도입한다.
Data의 variability를 모델링하기 위해 high-level latent variable을 사용하는 걸 제안한다.
highly structured는 dependency가 복잡함을 말하는 것 같고
high-level은 추상화 수준을 의미하는 것으로 보인다.
2. Background
2.1 Sequence modelling with Recurrent Neural Networks
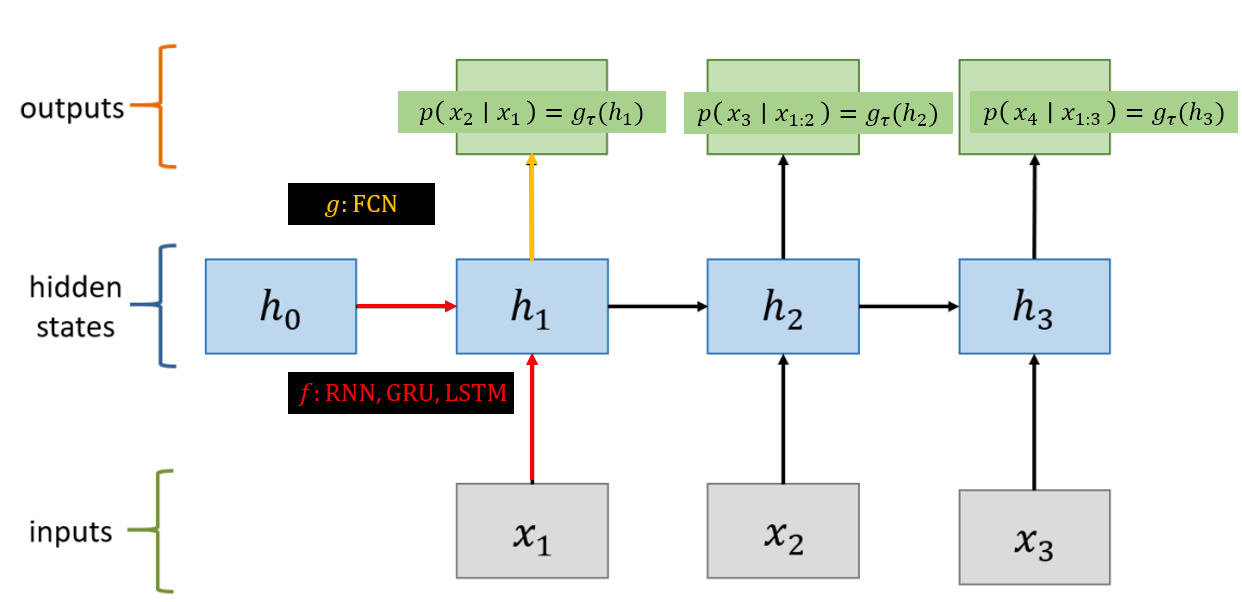
Likelihood maximization $p(x_1, \cdots, x_n)$으로 학습된다.
High-dimensional real valued sequence data를 학습할 땐, likelihood를 GMM으로 채택한다.
잠재적 issue로는 RNN이 $x_t$의 variability를 모델링하는 방식에 있다.
$f$를 deterministic function으로 구성하였기 때문에 $g$만으로 variability를 잡게 된다.
결국 noisy + highly structured sequential data를 RNN으로 모델링한다면 문제가 된다.
이런 종류의 데이터를 효율적으로 모델링하기 위해선, true hidden state와 noise hidden state를 확실하게 분리할 수 있는 능력이 있어야한다.
이건 거의 내가 작문한 수준인데 애매모호함을 아직 잘 이해하진 못했다.
2.2 Variational Autoencode
skip
3. Variational Recurrent Neural Network
이번 장에선, VAE와 DBM(HMM, Kalman filter)에 영감을 받은 VRNN을 소개하겠다.
- Latent variable과 Data간의 관계에 nonlinear dependency를 허용
- Latent variable간의 dependency를 명시함
3.1 Generation
| Prior | Generating Distribution | |
|---|---|---|
| VAE | $\mathbf{z} \sim \mathcal{N}\left(\mathbf 0, I)\right)$ | $\mathbf{x} \mid \mathbf{z} \sim \mathcal{N}\left(\boldsymbol{\mu}(\mathbf z), \text{diag}(\boldsymbol{\sigma}(\mathbf z) ^ 2)\right)$ |
| VRNN | $\mathbf{z}_{t} \sim \mathcal{N}\left(\boldsymbol{\mu}_{0, t}, \operatorname{diag}\left(\boldsymbol{\sigma}_{0, t}^{2}\right)\right),\\ \text { where }\left[\boldsymbol{\mu}_{0, t}, \boldsymbol{\sigma}_{0, t}\right]=\varphi_{\tau}^{\text {prior }}\left(\mathbf{h}_{t-1}\right)$ | $\mathbf{x}_{t} \mid \mathbf{z}_{t} \sim \mathcal{N}\left(\boldsymbol{\mu}_{x, t}, \operatorname{diag}\left(\boldsymbol{\sigma}_{x, t}^{2}\right)\right), \\\text { where }\left[\boldsymbol{\mu}_{x, t}\ \boldsymbol{\sigma}_{x, t}\right]=\varphi_{\tau}^{\operatorname{dec}}\left(\varphi_{\tau}^{\mathbf{z}}\left(\mathbf{z}_{t}\right), \mathbf{h}_{t-1}\right)$ |
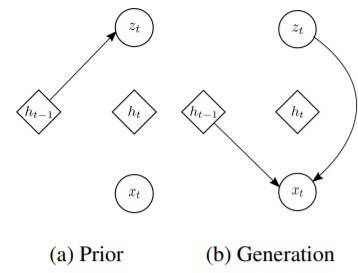
추가로 RNN의 update를 하게 된다.
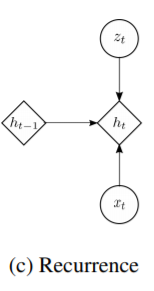
NOTE
$\varphi_{\tau}^{\mathbf{x}}$와 $\varphi_{\tau}^{\mathbf{z}}$는 feature extractor로 complex sequence 학습에 중요하다.
$h_t$는 $\mathbf x_{\leq t}, \mathbf z_{\leq t}$의 함수이기 때문에 암묵적으로 generative model의 factorization은
3.2 Inference
| Approximated posterior | |
|---|---|
| VAE | $\mathbf{z} \mid \mathbf{x} \sim \mathcal{N}\left(\boldsymbol{\mu}(\mathbf x), \text{diag}(\boldsymbol{\sigma}(\mathbf x) ^ 2)\right)$ |
| VRNN | $\mathbf{z}_{t} \mid \mathbf{x}_{t} \sim \mathcal{N}\left(\boldsymbol{\mu}_{z, t}, \operatorname{diag}\left(\boldsymbol{\sigma}_{z, t}^{2}\right)\right),\\ \text { where }\left[\boldsymbol{\mu}_{z, t}, \boldsymbol{\sigma}_{z, t}\right]=\varphi_{\tau}^{\mathrm{enc}}\left(\varphi_{\tau}^{\mathbf{x}}\left(\mathbf{x}_{t}\right), \mathbf{h}_{t-1}\right)$ |
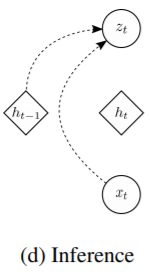
Note that we implicitly assume that
3.3 Learning
4. Experiment Settings
연설 오디오 데이터셋은 $\mathbf x_t = \left[\begin{array}{l}
x_{t, 1} \\
\cdots \\
x_{t, 200}
\end{array}\right]$으로 구성되어 있고 $t$ 시점에 대응하는 time interval에서의 amplitude의 연속적 기록이다.
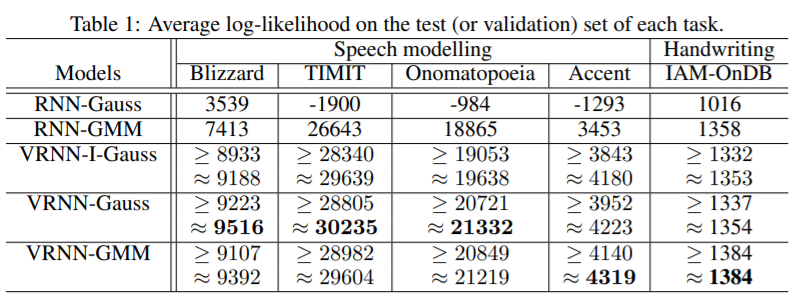
RNN-Gaussian과 RNN-GMM의 likelihood는 unbiased estimate이 되지만 VRNN 계열은 ELBO의 estimate만 가능하다.
Approximate 표기는 importance sampling을 활용하여 likelihood를 approximate한 결과이다.
RNN과 달리 VRNN은 unimodal gaussian을 data likelihood로 사용해도 잘되는 걸 볼 수 있다.
Latent variable이 complex sequential data를 모델링하는데 도움이 된다는 것을 알 수 있다.
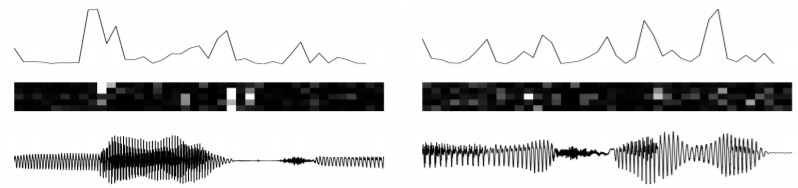
첫행은 $\delta_{t}=\sum_{j}\left(\boldsymbol{\mu}_{z, t}^{j}-\boldsymbol{\mu}_{z, t-1}^{j}\right)^{2}$ ; latent variable의 (variational parameter의) 변화
두번째 행은 KL-divergence의 변화
세번째 행은 original input이다.
- 세번째 행과 첫번째 행
- 음성의 (시각적, 주관적) 모드 변화에 latent variable의 변화가 있음을 알 수 있다.
- 첫번째 행과 두번째 행
- latent variable의 변화가 RNN dynamics의 변화를 만들어서 prior의 modality를 바꾼다.