0. Abstract

Identification of dynamic sequential plan 문제는 Identification of sequential plans 문제임을 보일 것이다.

거기서 거기 처럼 보이는데…

1. Introduction

연구의 동기는 Pearl & Robins, 1995, Dawid & Didelez, 2005에서

medical treatment $X_1, \cdots X_k$
observation $Z_1, \cdots , Z_k$
outcome variable $Y$

상황에서 effect of sequential treatment $X_1, \cdots X_k$ on $Y$를 estimate하는 데에 관심이 있었다.

이 논문에서는 DSPI 문제가 이미 잘 연구된 CEI 문제임을 보이겠다.

Pearl의 4.2에서, D(S)PI의 필요충분조건이 $P_{x}(y \mid z)$의 identifiability라고 했었지만, Tian, 2004, Shpitser and Pearl, 2006a의 complete identification 알고리즘이 개발되면서 이는 충분조건임을 보이겠다.

2. Previous Work and Notation

Causal DAG는 joint distribution $P(v)=P\left(v_{1}, \ldots, v_{n}\right)$을 factorize한다.

$P(v)=\prod_{i} P\left(v_{i} \mid p a_{i}\right)$

Regime indicator $\sigma_{V_{i}}$는 intervention의 종류를 나타내는 데 사용된다.

Idle regime : $P\left(v_{i} \mid p a_{i} ; \sigma_{V_{i}}=\emptyset\right)=P\left(v_{i} \mid p a_{i}\right)$
Atomic intervention : $P\left(v_{i} \mid p a_{i} ; \sigma_{V_{i}}=d o\left(v_{i}^{}\right)\right)=\delta\left(v_{i}, v_{i}^{}\right)$
Conditional intervention : $P\left(v_{i} \mid p a_{i} ; \sigma_{V_{i}}=\operatorname{do}(g(c))\right)=\delta\left(v_{i}, g(c)\right)$
Random intervention : $P\left(v_{i} \mid p a_{i} ; \sigma_{V_{i}}=d_{C}\right)=P^{*}\left(v_{i} \mid c\right)$

where $C$ is the set of previous variables

Sequential decision problem에서 (potential outcome framework)

control(action) variables $X = \{ X_i\} \subset V$는 intervention의 대상이다.
response(outcome) variable $Y \in V$는 관심의 대상이다.
covariates $Z = V \setminus [X \cup \{ Y\} ]$은 나머지 변수들이다.
변수의 관측 순서는 $\left(L_{1}, X_{1}, \ldots, L_{K}, X_{K}, Y\right)$이다. where $L_{i} \subset Z$
Let $\bar{X}_{i}=\left(X_{1}, \ldots, X_{i}\right)$ and $\bar{L}_{i}=\left(L_{1}, \ldots, L_{i}\right)$
Given an intervention strategy $\sigma_{X}=\left\{\sigma_{X_{i}}\right\}$, simple stability says
$L_i \perp \sigma_{X_i} \mid \bar{L}_{i-1}, \bar{X}_{i-1} \\ Y \perp \sigma_{X} \mid \bar{L}_{K}, \bar{X}_{K}$
Simple stability는 직감적으로 intervention은 독립적인 메커니즘이다를 의미한다.
이게 유지될 때, G-formula로 intervention distribution을 구할 수 있다.
$P\left(y ; \sigma_{X}\right)=\sum_{x, z} P(y \mid x, z) \prod_{i} P\left(l_{i} \mid \bar{l}_{i-1}, \bar{x}_{i-1}\right) \prod_{i} P\left(x_{i} \mid \bar{x}_{i-1}, \bar{l}_{i} ; \sigma_{X_{i}}\right)$

Unobserved confounder가 있을 때, simple stability는 유지되지 않고 G-formula는 문제가 생긴다.

3. Problem Formulation

Sequential decision problem에서

모든 변수가 observable이라 가정하고, $Z := V \setminus \{X \cup Y \}$ 라고 하자.
Given an intervention strategy $\sigma_{X}=\left\{\sigma_{X_{i}}\right\}$,
$P\left(v ; \sigma_{X}\right) =\prod_{i} P\left(y_{i} \mid p a_{y_{i}}\right) \prod_{i} P\left(z_{i} \mid p a_{z_{i}}\right) \prod_{i} P\left(x_{i} \mid p a_{x_{i}} ; \sigma_{X_{i}}\right)$
이는 CBN의 modularity assumption으로 나오는 equation이다.
결국, intervention distribution on $Y$는
$P\left(y ; \sigma_{X}\right)=\sum_{x, z} \prod_{i} P\left(y_{i} \mid p a_{y_{i}}\right) \prod_{i} P\left(z_{i} \mid p a_{z_{i}}\right)\prod_{i} P\left(x_{i} \mid p a_{x_{i}} ; \sigma_{X_{i}}\right)$
CBN이 암시하는 conditional independence에 의해 G-formula가 유도될 수 있다.

일반적으로, unobserved variable 때문에 confounding effect에 대해 신경써야한다.
Let $V = Y \cup Z \cup X$ and $U=\left\{U_{1}, \ldots, U_{n^{\prime}}\right\}$
Given an intervention strategy $\sigma_{X}=\left\{\sigma_{X_{i}}\right\}$,
$P(v)=\sum_{u} \prod_{\left\{i \mid V_{i} \in V\right\}} P\left(v_{i} \mid p a_{v_{i}}\right) \prod_{\left\{i \mid U_{i} \in U\right\}} P\left(u_{i} \mid p a_{u_{i}}\right)$
결국, intervention distribution on $Y$는
$P\left(y ; \sigma_{X}\right)=\sum_{x, z, u} \prod_{i} P\left(y_{i} \mid p a_{y_{i}}\right) \prod_{i} P\left(z_{i} \mid p a_{z_{i}}\right) \prod_{i} P\left(x_{i} \mid p a_{x_{i}} ; \sigma_{X_{i}}\right) \prod_{i} P\left(u_{i} \mid p a_{u_{i}}\right)$
CBN이 암시하는 conditional independence에 의해 Dawid & Didelez, 2005이 확장했던 G-formula에 대응한다.
이 경우엔, intervention distribution에 unobserved variable $U$가 껴있어서 identifiability에 대한 질문이 생긴다.

Definition 1 [Plan Identifiability]

A sequential plan is said to be identifiable if $P(y; \sigma_X)$ is uniquely computable from $P(v)$

4. Identification of Sequential Plans

Assumption 1

$P\left(x_{i} \mid p a_{x_{i}} ; \sigma_{X_{i}}\right)$ does not depend on unobserved variables.

Under Assumption 1, intervention distribution on $Y$ becomes

$\begin{aligned} P\left(y ; \sigma_{X}\right)& =\sum_{x, z, u} \prod_{i} P\left(y_{i} \mid p a_{y_{i}}\right) \prod_{i} P\left(z_{i} \mid p a_{z_{i}}\right) \prod_{i} P\left(x_{i} \mid p a_{x_{i}} ; \sigma_{X_{i}}\right) \prod_{i} P\left(u_{i} \mid p a_{u_{i}}\right) \\ &= \sum_{x, z} \prod_{i} P\left(x_{i} \mid p a_{x_{i}} ; \sigma_{X_{i}}\right) \sum_{u} \left( \prod_{i} P\left(y_{i} \mid p a_{y_{i}}\right) \prod_{i} P\left(z_{i} \mid p a_{z_{i}}\right) \prod_{i} P\left(u_{i} \mid p a_{u_{i}}\right) \right) \\ &= \sum_{x, z} \prod_{i} P\left(x_{i} \mid p a_{x_{i}} ; \sigma_{X_{i}}\right) P_{x}(y, z) \end{aligned}$

즉, $P\left(y ; \sigma_{X}\right)$의 identifiability의 충분조건은 $P_{x}(y, z)$이 identifiable한 것이다.

일반적으로, $P_{x}(y, z)$가 identifiable하지 않더라도 $P\left(y ; \sigma_{X}\right)$가 identifiable할 수 있다.

위의 derivation의 두번째 등식에서 특정 $Z_i$가 $P\left(z_{i} \mid p a_{z_{i}}\right)$ factor에서만 등장했다면 sumout이 될 것이고 이는 더 강한 identification criterion을 준다.

Proposition 1 [Simple sufficient criterion ; Dawid & Didelez, 2005]

If all the parents of action $X$ are observable, then $P(y; \sigma_X)$ is identifiable.

(Proof)

$\begin{aligned} P(v)&=\sum_{u} \prod_{\left\{i \mid V_{i} \in V\right\}} P\left(v_{i} \mid p a_{v_{i}}\right) \prod_{\left\{i \mid U_{i} \in U\right\}} P\left(u_{i} \mid p a_{u_{i}}\right) \\ &= \prod_{i} P\left(x_{i} \mid p a_{x_{i}}\right) \sum_{u}\left( \prod_{i} P\left(z_{i} \mid p a_{z_{i}}\right) \prod_{i} P\left(y_{i} \mid p a_{y_{i}}\right) \prod_{\left\{i \mid U_{i} \in U\right\}} P\left(u_{i} \mid p a_{u_{i}}\right)\right) \\ &= \prod_{i} P\left(x_{i} \mid p a_{x_{i}}\right) P_{x}(y, z) \\ \\ P_{x}(y, z)&=\frac{p(x, y, z)}{\prod_{i} P\left(x_{i} \mid p a_{x_{i}}\right)} \\ &= \frac{\prod_{\{i \mid V_i \in X \cup Y \cup Z\}}p(v_i \mid \bar v_{i-1})}{\prod_{i} P\left(x_{i} \mid p a_{x_{i}}\right)} \quad \text{where $V_i$ denote ordered observed variable} \\ &= \prod_{\left\{i \mid V_{i} \in Y \cup Z\right\}} P\left(v_{i} \mid \bar{v}_{i}\right) \quad \because pa_{x_i} \subseteq V \end{aligned}$

Hence, $P\left(y ; \sigma_{X}\right)=\sum_{x, z} \prod_{i} P\left(x_{i} \mid p a_{x_{i}} ; \sigma_{X_{i}}\right) \prod_{\left\{i \mid V_{i} \in Y \cup Z\right\}} P\left(v_{i} \mid \bar{v}_{i}\right)$

Theorem 1에 사용될 notation을 짚고 넘어가자.

${}^\forall S \subseteq V$, let $Q\left[S\right]$ denote intervention distribution of $S$ under atomic intervention $v \setminus s$

$\begin{aligned} Q[S](v)&=P_{v \backslash s}(s) \\ &= \sum_{u} \prod_{\left\{i \mid V_{i} \in S\right\}} P\left(v_{i} \mid p a_{v_{i}}\right) \prod_{\left\{i \mid U_{i} \in U\right\}} P\left(u_{i} \mid p a_{u_{i}}\right) \\ & =: Q[S] \quad \text{for convenience} \end{aligned}$

Then, $P\left(y ; \sigma_{X}\right)=\sum_{x, z} \prod_{i} P\left(x_{i} \mid p a_{x_{i}} ; \sigma_{X_{i}}\right) Q\left[Y \cup Z\right]$

Let $G_{\sigma_{X}}$ denote the manipulated graph under the intervention strategy $\sigma_X$

If $\sigma_{X_{i}}=d o\left(x_{i}\right)$, then cut off all the arrows entering $X_i$

If $\sigma_{X_{i}}=d o\left(g_i(c_{i})\right)$ or $\sigma_{X_{i}}=d_{C_{i}}$, then cut off all the arrows entering $X_i$ and add $C_i \rightarrow X_i$

Theorem 1

Let $Z_D$ be the set of variables in $Z$ that are ancestors of $Y$ in $G_{\sigma _X}$

Then, $P\left(y ; \sigma_{X}\right)$ is identifiable if the causal effects $Q\left[Y \cup Z_{D}\right]=P_{x, z \backslash z_{D}}\left(y, z_{D}\right)$ is identifiable.

(Proof)

Let $X_D$ be the set of variables in $X$ that are ancestors of $Y$ in $G_{\sigma _X}$

Then, all the non ancestors of $Y$ can be summed out as

$\begin{aligned} P\left(y ; \sigma_{X}\right)&=\sum_{x\in X, z\in Z} \prod_{i} P\left(x_{i} \mid p a_{x_{i}} ; \sigma_{X_{i}}\right) Q\left[Y \cup Z\right] \\ &= \sum_{x_d , z_d} \prod_{i} P\left(x_{i} \mid p a_{x_{i}} ; \sigma_{X_{i}}\right) Q\left[Y \cup Z_D\right] \\ &=\sum_{x_d , z_d} \prod_{\left\{i \mid X_{i} \in X_{D}\right\}} P\left(x_{i} \mid p a_{x_{i}} ; \sigma_{X_{i}}\right) P_{x, z \setminus z_{D}}\left(y, z_{D}\right) \end{aligned}$

Factor가 sum out되는 걸 생각하면 이 증명은 굉장히 clear하나 찜찜했던 부분이 있었다.

Summation에서 $z\setminus z_d$에 대한 명시가 없기 때문에 $P_{x, z \setminus z_{D}}\left(y, z_{D}\right)$이 well-defined일려면, $z\setminus z_d$의 값과 상관없는 distribution이여야 한다.

그래프적으로 생각하면 $Z_D$의 조상이 $Z\setminus Z_D$에 속할 일이 없다.

그랬다면, $Y$의 ancestor로서 $Z_D$에 속했을 테니 말이다.

추가로 $Q\leftS \right$는 $Pa^+(S)$의 함수라는 성질 때문에 $z\setminus z_d$의 값과 상관없는 distribution이다.

Theorem 1의 condition이 충분조건일 뿐만 아니라 필요조건이라고 생각된다.

Let $Z_{\sigma_{X_{D}}}$ be the set of $Z$ variables that appear in $ \prod_{\left\{i \mid X_{i} \in X_{D}\right\}} P\left(x_{i} \mid p a_{x_{i}} ; \sigma_{X_{i}}\right)$

Then, $ \prod_{\left\{i \mid X_{i} \in X_{D}\right\}} P\left(x_{i} \mid p a_{x_{i}} ; \sigma_{X_{i}}\right)$ is a function of $X_D , Z_{\sigma_{X_D}}$

$\begin{aligned} P\left(y ; \sigma_{X}\right) &= \sum_{x_d , z_d} \prod_{\left\{i \mid X_{i} \in X_{D}\right\}} P\left(x_{i} \mid p a_{x_{i}} ; \sigma_{X_{i}}\right) Q\left[Y \cup Z_D\right] \\ &= \sum_{x_{D}, z_{\sigma_{X_D}}} \prod_{\left\{i \mid X_{i} \in X_{D}\right\}} P\left(x_{i} \mid p a_{x_{i}} ; \sigma_{X_{i}}\right) \sum_{z_{D} \setminus z_{\sigma_{X}}} Q\left[Y \cup Z_{D}\right] \\ &=:\sum_{x_{D}, z_{\sigma_{X_D}}} \prod_{\left\{i \mid X_{i} \in X_{D}\right\}} g(x_D, z_{\sigma_{X_D}}) \sum_{z_{D} \setminus z_{\sigma_{X}}} Q\left[Y \cup Z_{D}\right] \end{aligned}$

즉, $\sum_{z_{D} \setminus z_{\sigma_{X}}} Q\left[Y \cup Z_{D}\right]$이 identifiable하면 $P\left(y ; \sigma_{X}\right)$이 identifiable하다.

필요조건인 plan에 종속된 변수는 애초에 sum out의 기회가 없기 떄문이다.

추가로 $Z_D$는 애초에 $Y$의 조상으로 이뤄지기 때문에 sum-out이 일어날 일이 없다.

이에 대한 일반적인 이야기는 Huang and Valtorta, 2006; Lemma 11

그 결과, $\sum_{z_{D} \setminus z_{\sigma_{X}}} Q\left[Y \cup Z_{D}\right]$의 identifiability와 $Q\left[Y \cup Z_{D}\right]$의 identifiability는 동치이다.

Theorem 1이 필요충분조건이다.
결국 DSPI는 $Q\left[Y \cup Z_{D}\right]$ identification 문제이다.

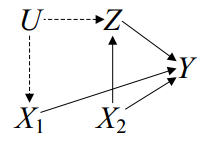
이 문제는 $Q\left[Y \cup Z\right]$를 identify하는 문제이다.
Observational distribution $P(v)=P\left(y \mid x_{1}, x_{2}, z\right) P\left(x_{2}\right) Q\left[\left\{Z, X_{1}\right\}\right]$
- where $Q\left[\left\{Z, X_{1}\right\}\right]=\sum_{u} P\left(z \mid x_{2}, u\right) P\left(x_{1} \mid u\right) P(u)$
We want to compute
$P\left(y ; \sigma_{X_{1}}, \sigma_{X_{2}}\right) =\sum_{x_{1}, x_{2}, z} P\left(x_{1} ; \sigma_{X_{1}}\right) P\left(x_{2} ; \sigma_{X_{2}}\right) P\left(y \mid x_{1}, x_{2}, z\right) Q\left[\{Z\}\right]$
Since
- $Q[\{Z\}]=\sum_{x_{1}} Q\left[\left\{Z, X_{1}\right\}\right]$
- $Q\left[\left\{Z, X_{1}\right\}\right]=P\left(z, x_{1} \mid x_{2}\right)$
we finally obtain

$P\left(y ; \sigma_{X_{1}}, \sigma_{X_{2}}\right) =\sum_{x_{1}, x_{2}, z} P\left(x_{1} ; \sigma_{X_{1}}\right) P\left(x_{2} ; \sigma_{X_{2}}\right) P\left(y \mid x_{1}, x_{2}, z\right) P\left(z \mid x_{2}\right)$

5. Discussion

5.1 Unconditional plans are easier

Dynamic plan을 identify하는 건 unconditional plan을 identify하는 것 보다 어렵다.

$\sigma_{X}^{\prime}$는 atomic intervention으로만 이루어진 경우, $G_{\sigma_{X}^{\prime}} \subset G_{\sigma_{X}}$ 이다.

그리고, $G_{\sigma_{X}^{\prime}}$에 대응하는 $Z_D’$는 $Z_D$의 subset이 된다. 이 경우, theorem 1을 적용시

$P\left(y ; \sigma_{X}^{\prime}\right)=P_{x}(y)=\sum_{z_{D}^{\prime}} Q\left[Y \cup Z_{D}^{\prime}\right]$

추가로, $Z_{D} \backslash Z_{D}^{\prime}$는 $X$를 거쳐야만 $Y$로 가는 path가 있기 때문에,

$Q\left[Y \cup Z_{D}^{\prime}\right]=\sum_{z_{D} \setminus z_{D}^{\prime}} Q\left[Y \cup Z_{D}\right]$

기존의 $Q\left[Y \cup Z_{D}\right]$에서 sum out이 이뤄진 형태이기 때문에 더 쉬운 문제이다.

예시 $P(v)=P\left(x_{2} \mid x_{1}, z\right) Q\left[\left\{X_{1}, Z, Y\right\}\right]$

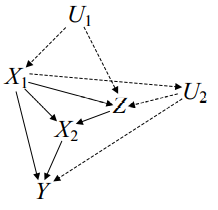
$\sigma_{X_{2}}=d o\left(g\left(x_{1}, z\right)\right)$인 경우, $Q\left [\{ Y, Z\} \right]$를 identify하는 문제인데 이는 identifiable하지 않다.

이에 대한 내용은 Huang and Valtorta, 2006에 나와있다.

$\sigma_{X_{2}}=d o\left(g\left(x_{1}\right)\right)$인 경우, $Q[\{Y\}]$를 identify하는 문제인데 이는 identifiable하다.

$\begin{aligned} P\left(y ; \sigma_{X_{1}}, \sigma_{X_{2}}=d_{X_{1}}\right) &= \sum_{x_{1}, x_{2}} P\left(x_{1} ; \sigma_{X_{1}}\right) P^{*}\left(x_{2} \mid x_{1}\right) Q[\{Y\}] \\ \\ Q\left[\left\{X_{1}, Z, Y\right\}\right] &=P(v) / P\left(x_{2} \mid x_{1}, z\right) \\ &=P\left(y \mid x_{1}, x_{2}, z\right) P\left(x_{1}, z\right) \\ \\ Q[\{Y\}] &=\frac{\sum_{z} Q\left[\left\{X_{1}, Z, Y\right\}\right]}{\sum_{y, z} Q\left[\left\{X_{1}, Z, Y\right\}\right]} \\ &=\sum_{z} P\left(y \mid x_{1}, x_{2}, z\right) P\left(z \mid x_{1}\right) \end{aligned}$

마지막 등식을 체계적으로 구하는 방법은…?

이 경우, unconditional plan은 바로 구할 수 있다.

$P_{x_{1}, x_{2}}(y)=Q[\{Y\}]=\sum_{z} P\left(y \mid x_{1}, x_{2}, z\right) P\left(z \mid x_{1}\right)$

5.2 Identification via conditional causal effects?

Pearl의 4.2에서, D(S)PI의 필요충분조건이 $P_{x}(y \mid z)$의 identifiability라고 했었지만 이는 single variable $X$에 대해서만 맞는 말이다.

single variable $X$에 대해서 Theorem 1을 적용시,

$\begin{aligned} P\left(y ; \sigma_{X}=d o(g(z))\right)&=\left.\sum_{z} P_{x}(y \mid z)\right|_{x=g(z)} P(z) \\ P\left(y ; \sigma_{X}=d_{Z}\right)&=\sum_{x, z} P_{x}(y \mid z) P^{*}(x \mid z) P(z) \end{aligned}$

결국, $P_{x}(y \mid z)$의 identifiability와 $P\left(y ; \sigma_{X}\right)$의 identifiability는 동치이다.

여러개의 variable $X$를 고려해보자.

Let $\sigma_{X_{i}}=\operatorname{do}\left(g_{i}\left(C_{i}\right)\right)$

Let $Z_{\sigma_{X}}=Z \cap\left(\cup_{i} C_{i}\right)$ be the set of conditioning variables in the strategy $\sigma_X$.

Pearl 2006은

$P\left(y ; \sigma_{X}\right)=\sum_{z_{\sigma_{X}}} P_{x_{z}}\left(y \mid z_{\sigma_{X}}\right) P_{x_{z}}\left(z_{\sigma_{X}}\right)$

임을 보이며, sequential conditional plan은 $P_{x}(y \mid z)$와 $P_{x}(z)$를 identify하는 문제라고 제안하였다.

그러나 이는 필요조건이 아니라는 걸 보이겠다. Theorem 1을 사용하면

$\begin{aligned} P\left(y ; \sigma_{X}\right)&=\sum_{x, z_{\sigma_{X}}} \delta\left(x_{i}, g_{i}\left(C_{i}\right)\right) P_{x}\left(y, z_{\sigma_{X}}\right) \\ &= \sum_{x, z_{\sigma_X}} \delta \left(x_{i}, g_{i}\left(C_{i}\right)\right) \sum_{z \setminus z_{\sigma_{X}}} Q\left[Y, Z \right] \end{aligned}$

로 표현할 수 있고, $Q\left [Y, Z \right]$에서 sum-out이 일어난다면 $P_{x}(y \mid z)$와 $P_{x}(z)$ identification이 불가능하더라도 $Q\left [Y, Z \right]$는 identifiable할 것이다.

예시 $P(v)=P\left(y \mid x_{1}, x_{3}, z_{3}\right) P\left(x_{3} \mid x_{2}, z_{3}\right) P\left(z_{1}\right) Q\left[\left\{X_{2}, Z_{3}\right\}\right] Q\left[\left\{X_{1}, Z_{2}\right\}\right]$

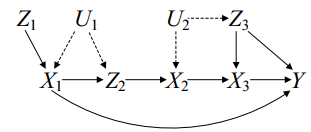
$\sigma_{X}=\left\{\sigma_{X_{1}}=\operatorname{do}\left(g_{1}\left(Z_{1}\right)\right), \sigma_{X_{2}}=d o\left(g_{2}\left(Z_{2}\right)\right), \sigma_{X_{3}}= \operatorname{do}\left(g_{3}\left(Z_{3}\right)\right)\right\}$
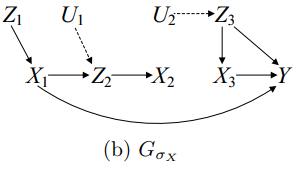
$X_D = \{ X_1, X_3\}, $$Z_{D}=\left\{Z_{1}, Z_{3}\right\}$
Theorem 1이 말하길 $Q\left[\left\{Y, Z_{1}, Z_{3}\right\}\right]$을 identify하면 된다.
$Q\left[\left\{Y, Z_{1}, Z_{3}\right\}\right] = Q\left[\left\{Y\right\}\right] Q\left[\left\{Z_{1}\right\}\right] Q\left[\left\{ Z_{3}\right\}\right]$
$Q\left[\left\{Z_{3}\right\}\right]=\sum P\left(z_{3} \mid u_{2}\right) P\left(u_{2}\right)=P\left(z_{3}\right)$

$\begin{aligned} P\left(y ; \sigma_{X}\right) &=\sum_{x_{d}, z_{d}} \prod_{i} \delta\left(x_{i}, g_{i}\left(z_{i}\right)\right) Q\left[\left\{Y\right\}\right] Q\left[\left\{Z_{1}\right\}\right] Q\left[\left\{ Z_{3}\right\}\right] \\ &= \sum_{x_{1}, x_{3}, z_{1}, z_{3}} \delta\left(x_{1}, g_{1}\left(z_{1}\right)\right) \delta\left(x_{3}, g_{3}\left(z_{3}\right)\right) P\left(y \mid x_{1}, x_{3}, z_{3}\right)P\left(z_{1}\right) Q\left[\left\{Z_{3}\right\}\right] \\ &= \sum_{z_{1}, z_{3}} P\left(y \mid g_{1}\left(z_{1}\right), g_{3}\left(z_{3}\right), z_{3}\right) P\left(z_{1}\right) P\left(z_{3}\right) \end{aligned}$

반면에 Pearl 2006은 $P_{x_{1} x_{2} x_{3}}\left(y, z_{1}, z_{2}, z_{3}\right)=Q\left[\left\{Y, Z_{1}, Z_{2}, Z_{3}\right\}\right]$을 identify해야한다고 했다.

$\begin{aligned} P_{x_{1} x_{2} x_{3}}\left(y, z_{1}, z_{2}, z_{3}\right)&=P\left(y \mid x_{1}, x_{3}, z_{3}\right) P\left(z_{1}\right) Q\left[\left\{Z_{3}\right\}\right] Q\left[\left\{Z_{2}\right\}\right] \\ &=P\left(y \mid x_{1}, x_{3}, z_{3}\right) P\left(z_{1}\right) P\left(z_{3}\right) Q\left[\left\{Z_{2}\right\}\right] \end{aligned}$

$Q\left[\left\{Z_{2}\right\}\right]$는 identifiable하지 않기 떄문에 $P_{x_{1} x_{2} x_{3}}\left(y, z_{1}, z_{2}, z_{3}\right)$는 identifiable하지 않다.
좀 더 자세하게 말하면,
- $P_{x_{1} x_{2} x_{3}}\left(y \mid z_{1}, z_{2}, z_{3}\right)=P\left(y \mid x_{1}, x_{3}, z_{3}\right)$ 이건 identifiable했는데
- $P_{x_{1} x_{2} x_{3}}\left(z_{1}, z_{2}, z_{3}\right)=P\left(z_{1}\right) P\left(z_{3}\right) Q\left[\left\{Z_{2}\right\}\right]$ 이게 identifiable하지 않았다.

Study Repo

Identifying Dynamic Sequential Plans