0. Abstract

DTR은 decision rule들의 sequence이고 환자의 이전 치료와 covariate history에 기반해 어떻게 치료할 지를 명시한다.

DTR은 만성(chronic) 질환 관리에 효과적이고, 개인화된 의사결정에 핵심적이다.

이 논문에선, observational data도 활용 가능할 때, optimal DTR을 찾는 online RL 문제를 다룬다.

이전 history를 사용하지 않고서 online setting에서 near-optimal DTR에 도달하는 adaptive algorithm을 개발했다.
Confounded observational data로부터 유의미한 regret의 upper/lower bound를 도출한다.
이들을 엮어서 confounded observational data도 활용하여 optimal DTR을 학습하는 RL algorithm을 개발했다.

1. Introduction

의료 실무에서 환자는 일반적으로 여러단계에 걸쳐 치료를 받는다.

의사는 반복적으로 환자의 state(바이러스 수치, 진단결과)에 맞춰서 treatment를 조정하게 된다.

DTR은 longitudinal setting에서 personalized treatment의 매력적인 framework를 제공한다.

DTR은 adaptive treatment strategy, treatment policy로도 알려져있다.

DTR은 암, 당뇨, 정신병과 같은 만성질환의 개인화된 치료에 효과적이다.

예시

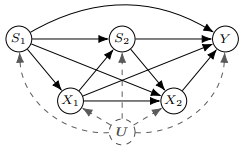
알코올 의존증 환자들의

condiition $S_1$에 기반하여
처방 $X_1$을 하고
효과가 있었냐 없었냐 $S_2$로 구분하고
초기 치료를 유지할 지 바꿀 지 $X_2$ 결정하여
환자의 12개월 간의 금주 비율 $Y$이 어떨 지에 대해 관심이 있다.
$U$는 unobserved confounder를 나타내고 환자에 대해 모르는 모든 요인들에 대한 요약이다.

DTR은 이들 전체의 SCM을 가르키고 treatment policy는 $X$를 결정짓는 SCM의 일부분을 가르킨다.

Policy learning in DTR은 $Y$를 최대화하는 optimal policy를 찾는 것이다.

Main challenge는 DTR의 parameter를 모르기 때문에 $E_{\boldsymbol{\pi}}\left[Y\right]$를 직접적으로 계산할 수 없다.

Causal Inference 쪽에서 대부분의 work은 causal assumption과 finite observational data를 갖고서 $E_{\boldsymbol{\pi}}\left[Y\right]$를 identify하는 것에 집중한다.

optimal policy를 찾진 않음!

Unobserved confounder가 없으면($\approx$ conditional ignorability), sequential backdoor criterion으로 estimate할 수 있다.

Ignorability가 유지될 때, $E_{\boldsymbol{\pi}}\left[Y\right]$를 estimate하는 효율적인 방법들이 있다.

Propensity Score [26]
Inverse probability of treatment weighting [21, 25]
Q-learning [31, 20]

Randomized experiment로 estimate하는 논문도 있으나 비용적인 문제가 있다.

RL은 exploration과 exploitation의 balancing으로 효율적으로 policy learning을 한다.

DTR learning이라고 표현됐는데, Model based RL이라면 맞는 표현일지도…?

RL은 일반적인 MDP 셋팅에서 잘 작동한다.

이의 variation으로는 multi-armed bandits, partially-observable MDP, factored MDPs가 있다.

우리의 focus는 observational data도 활용하면서 policy를 학습하는 것이다.

CI 관점에서 어려운 것은 unobserved confounder 때문이다.

RL 관점에서 어려운 것은 이전의 treatment $X_1$이 최종 outcome $Y$에 영향을 주는 구조이다.

비록 Thompson Samling과 같은 heuristic approach가 있으나, 모든 observational data를 망각(oblivious)하기 때문에 optimal은 아니다.

이 부분은 잘 모르는 데 다시 보도록 하자. see [35]

이 논문은 이러한 어려움들을 극복해내는 것이다.

이 문제를 large confounded observational data를 활용하면서 unknown DTR을 최적화할 수 있는 RL strategy를 도입하여 해결하겠다.

Contribution

UC-DTR : observational data없이, DTR setting에서 near-optimal regret bound에 도달하는 알고리즘
Upper/Lower bound : DTR 구조에 기반해서(Thm 5, 6), observational data를 활용한 bound 도출
$\text { UC }^{c}-\text { DTR }$: 효율적으로 bound를 활용하여 online setting에서 학습을 가속화한다.

결과에 대한 검증은 randomly generated DTR과 암치료 데이터에서 이루어진다.

1.1 Preliminaries

skip

2. Optimizing Dynamic Treatment Regimes

Definition 1 (DTR의 SCM 버전)

DTR is a SCM $\langle\boldsymbol{U}, \boldsymbol{V}, \boldsymbol{F}, P(\boldsymbol{u})\rangle$ where $\boldsymbol{V}=\left\{\overline{\boldsymbol{X}}_{K}, \overline{\boldsymbol{S}}_{K}, Y\right\}$

$K$는 total stage를 의미함

For $k=1, \cdots , K$

$X_k$ is a finite decision decided by a behavior policy $x_{k} \leftarrow f_{k}\left(\overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k-1}, \boldsymbol{u}\right)$
$S_k$ is a finite state decided by a transition function $s_{k} \leftarrow \tau_{k}\left(\overline{\boldsymbol{x}}_{k-1}, \overline{\boldsymbol{s}}_{k-1}, \boldsymbol{u}\right)$
$Y$ is the primary outcome at the final stage $K$ decided by a reward function $y \leftarrow r\left(\overline{\boldsymbol{x}}_{K}, \overline{\boldsymbol{s}}_{K}, \boldsymbol{u}\right)$

DTR $M^*$는 observational distribution $P\left(\overline{\bar{x}}_{K}, \overline{\boldsymbol{s}}_{K}, y\right)$를 유도한다.

Policy들의 collection은 policy space $\Pi$를 정의한다.

Policy $\boldsymbol\pi$는 interventional distribution over $\overline{\boldsymbol{X}}_{K}, \overline{\boldsymbol{S}}_{K}, Y$를 유도한다.

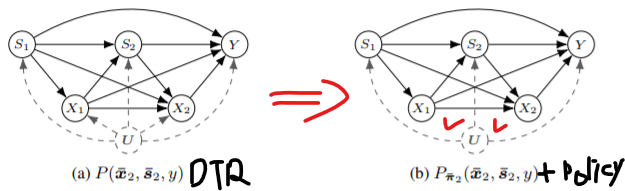
$P_{\pi}\left(\overline{\boldsymbol{x}}_{K}, \overline{\boldsymbol{s}}_{K}, y\right)=P_{\overline{\boldsymbol{x}}_{K}}\left(y \mid \overline{\boldsymbol{s}}_{K}\right) \prod_{k=0}^{K-1} P_{\overline{\boldsymbol{x}}_{k}}\left(s_{k+1} \mid \overline{\boldsymbol{s}}_{k}\right) \pi_{k+1}\left(x_{k+1} \mid \overline{\boldsymbol{s}}_{k+1}, \overline{\boldsymbol{x}}_{k}\right)$

$M^{\star} + \pi$에 따라 expected reward $V_{\boldsymbol{\pi}}\left(M^{\star}\right)=E_{\boldsymbol{\pi}}[Y]$ 이 주어진다.

우리는 optimal policy $\pi^{\star} := \arg \max _{\boldsymbol{\pi} \in \boldsymbol{\Pi}} V_{\boldsymbol{\pi}}\left(M^{\star}\right)$ 를 찾는 게 목표이다.

Decision theory에서 random policy들만으로 구성된 policy space나 deterministic policy로만 구성된 policy space나 optimal value가 같다는 게 알려져있으니 편의를 위해 deterministic policy만으로 구성된 policy space를 사용하겠다.

Unknown DTR $M^{*}$를 학습하고 싶다.

Agent(의사)는 반복된 experiment들로 학습한다.

이 때 각 episode $t$는 DTR과 policy의 realization이다.

$T$번 째 episode까지의 regret을 $R(T)=\sum_{t=1}^{T}\left(V_{\pi^{*}}\left(M^{\star}\right)-Y^{t}\right)$로 표기하자.

Agent가 optimal policy $\pi^*$에 수렴함에 따라 $\lim _{T \rightarrow \infty} E[R(T)] / T=0$을 기대한다.

2.1 The UC-DTR Algorithm

UC-DTR은 unknown DTR을 최적화하는 RL 알고리즘이다.

Domain $\boldsymbol{\mathcal{S}}, \boldsymbol{\mathcal{X}}$ 상의 지식만 갖고서 total regret의 near optimal에 도달한다는 것을 증명하겠다.

도메인 상의 지식이 뭘 말하는 건지 아직 모름

Step 1~3 : 이전 에피소드들에서 얻어진 experimental samples들로 empirically estimate

Step 4 : 타당한(emprical에서 크게 벗어나지 않은) DTR 후보들의 집합 $\mathcal{M}_{t}$ 정의

Step 5 : 가장 optimistic한 DTR $M_t \in \mathcal{M}_{t}$ 에서 optimal policy $\boldsymbol{\pi}_{t}$ 를 찾기

2.1.1 Finding Optimistic DTRs

Bellman equation은 DTR이 고정됐을 때 optimal policy를 찾는 걸 가능하게 해준다.

결국에 Step 5에서 가장 중요한 건 optimistic DTR을 찾으면 된다.

이 문제를 풀기위해 standard dynamic programming planner[5]를 확장하는 방법을 도입한다.

우선 continuous decision space $\overline{\boldsymbol{\mathcal{X}}}^{+}=\overline{\boldsymbol{\mathcal{X}}}_{K}^{+}$를 고려하자.

original $\overline{\boldsymbol{\mathcal{X}}}_{K}$는 가산+이산 set임.

${}^{\forall} \overline{\boldsymbol{x}}_{k} \in \overline{\boldsymbol{\mathcal{X}}}_{k}$, $^{\exists} \overline{\boldsymbol{x}}^+_{k} \in \overline{\boldsymbol{\mathcal{X}}}^+_{k}$ s.t.

$P_{\overline{\boldsymbol{x}}_{k}^+}\left(s_{k+1} \mid \overline{\boldsymbol{s}}_{k}\right) = P_{\overline{\boldsymbol{x}}_{k}}\left(s_{k+1} \mid \overline{\boldsymbol{s}}_{k}\right) \\ E_{\overline{\boldsymbol{x}}_{K}^+}\left[Y \mid \overline{\boldsymbol{s}}_{K}\right] = E_{\overline{\boldsymbol{x}}_{K}}\left[Y \mid \overline{\boldsymbol{s}}_{K}\right]$

$^\forall \boldsymbol\pi_{+} \text { on } M_{+}$, $^\exists\boldsymbol{\pi}_{t} \text{ on } M_t$ s.t.

$P_{\boldsymbol\pi_{+}}\left(s_{k+1} \mid \overline{\boldsymbol{s}}_{k}\right) = P_{\boldsymbol\pi_{t}}\left(s_{k+1} \mid \overline{\boldsymbol{s}}_{k}\right)$

그래서 Step 5는 extended DTR $M_+$에서 optimal policy를 찾는 문제와 동일하다.

Let $V^{\star}(\overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k-1})$ denote the optimal value $E_{\pi_{+}^{\star}}\left[Y \mid \overline{\boldsymbol s}_{k}, \overline{\boldsymbol x}_{k-1}\right]$.

Then, the Bellman equation on $M_+$ for $k=1, \cdots, K-1$ is defined as follows:

$\begin{aligned} V^{*}\left(\overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k-1}\right)&= \max _{x_{k}}\left\{\max _{P_{\overline{\boldsymbol{x}}_{k}}\left(\cdot \mid \overline{\boldsymbol{s}}_{k}\right) \in \mathcal{P}_{k}}\left\{\sum_{s_{k+1}} V^{*}\left(\overline{\boldsymbol{s}}_{k+1}, \overline{\boldsymbol{x}}_{k}\right) P_{\overline{\boldsymbol{x}}_{k}}\left(s_{k+1} \mid \overline{\boldsymbol{s}}_{k}\right)\right\}\right\} \\ V^{*}\left(\overline{\boldsymbol{s}}_{K}, \overline{\boldsymbol{x}}_{K-1}\right)&= \max _{x_{K}} \max_{E_{\overline{\boldsymbol{w}}_{K}}\left[Y \mid \overline{\boldsymbol{s}}_{K}\right] \in \mathcal{R}} E_{\overline{\boldsymbol{x}}_{K}}\left[Y \mid \overline{\boldsymbol{s}}_{K}\right] \end{aligned}$

where $\mathcal{R}, \mathcal{P}_{k}$ are the convex polytope of parameters $E_{\overline{\boldsymbol{x}}_{K}}\left[Y \mid \overline{\boldsymbol{s}}_{K}\right], P_{\overline{\boldsymbol{x}}_{k}}\left(s_{k+1} \mid \overline{\boldsymbol{s}}_{k}\right)$

이는 convex polytope 상에서의 linear programming으로 해결될 수 있다.

$\begin{aligned} V_{\boldsymbol \pi}( \overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k-1}) &= E_{\boldsymbol \pi} [Y \mid \overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k-1}] \\ &= \sum_{s_{k+1}}E_{\boldsymbol \pi} [Y \mid \overline{\boldsymbol{s}}_{k+1}, \overline{\boldsymbol{x}}_{k-1}] P_{\overline{\boldsymbol{x}}_{k}} (s_{k+1} \mid \overline{\boldsymbol{s}}_{k}) \quad \because\text{$\boldsymbol \pi$ is deterministic} \\ &= \sum_{s_{k+1}}E_{\boldsymbol \pi} [Y \mid \overline{\boldsymbol{s}}_{k+1}, \overline{\boldsymbol{x}}_{k}] P_{\overline{\boldsymbol{x}}_{k}} (s_{k+1} \mid \overline{\boldsymbol{s}}_{k}) \quad \because\text{$\boldsymbol \pi$ is deterministic} \\ &= \sum_{s_{k+1}}V_{\boldsymbol \pi}( \overline{\boldsymbol{s}}_{k+1}, \overline{\boldsymbol{x}}_{k})P_{\overline{\boldsymbol{x}}_{k}} (s_{k+1} \mid \overline{\boldsymbol{s}}_{k}) \end{aligned}$
Let $V^{*}\left(\overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k-1}\right) = \max_{\boldsymbol \pi} V_{\boldsymbol \pi} \left(\overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k-1}\right)$

Then $V^\star$ satisfies

$V^*_{\boldsymbol \pi}( \overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k-1}) = \max _{x_k}\sum_{s_{k+1}}V^*_{\boldsymbol \pi}( \overline{\boldsymbol{s}}_{k+1}, \overline{\boldsymbol{x}}_{k})P_{\overline{\boldsymbol{x}}_{k}} (s_{k+1} \mid \overline{\boldsymbol{s}}_{k})$

논문의 max에 $\mathcal{R}, \mathcal{P}_{k}$가 추가된 이유는 dynamics를 모르기 때문에 empirical에서 크게 벗어나지 않은 optimistic DTR 하에서 최대화하려는 의도이다.

2.2 Theoretical Analysis

UC-DTR의 asymptotic behavior를 알아보자.

모든 증명들은 appendix에 제공된다.

Theorem 1 (Upper bound)

The regret of UC-DTR is bounded by w/ probability $\geq 1-\delta$

$R(T) \leq12 K \sqrt{|\boldsymbol{\mathcal{S}}||\boldsymbol{\mathcal{X}}| T \log (2 K|\boldsymbol{\mathcal{S}} \| \boldsymbol{\mathcal{X}}| T / \delta)}+4 K \sqrt{T \log (2 T / \delta)}$

Theorem 2 (Gap-dependent upper bound)

Let $\mathbf{\Pi}^{-}$ denote the set of sub-optimal policies $\{\boldsymbol{\pi} \in \boldsymbol{\Pi}: V_{\boldsymbol{\pi}}\left(M^{\star}\right)<V_{\boldsymbol{\pi}^{\star}}\left(M^{\star}\right)\}$

Let $\Delta_{\boldsymbol{\pi}}=V_{\boldsymbol{\pi}^{}}\left(M^{}\right)-V_{\boldsymbol{\pi}}\left(M^{*}\right)$

Then, the expected regret of UC-DTR with parameter $\delta=\frac{1}{T}$ is bounded by

$E[R(T)] \leq \max _{\boldsymbol{\pi} \in \Pi^{-}}\left\{\frac{33^{2} K^{2}|\boldsymbol{\mathcal{S}}||\boldsymbol{\mathcal{X}}| \log (T)}{\Delta_{\pi}}+\frac{32}{\Delta_{\pi}^{3}}+\frac{4}{\Delta_{\pi}}\right\}+1$

Theorem 3 (Lower bound)

For any algorithm, there is a DTR $M$ with horizon $K$ s.t.

$E[R(T)] \geq 0.05 \sqrt{|\mathcal{S} \| \mathcal{X}| T} \quad \text{where $T\geq|\boldsymbol{\mathcal{S}} \| \boldsymbol{\mathcal{X}}|$}$

Theorem 1의 upper bound $\tilde{\mathcal{O}}(K \sqrt{|\boldsymbol{\mathcal{S}}||\boldsymbol{\mathcal{X}}| T})$가 이론적으로 도달할 수 있는 lower bound $\Omega(\sqrt{|\boldsymbol{\mathcal{S}}||\boldsymbol{\mathcal{X}}| T})$와 비슷하므로 UC-DTR은 near-optimal이다.

3. Learning from Confounded Observations

Theorem 1~3은 DTR에서 online learning의 bound 계산에 $\boldsymbol{\mathcal S}, \boldsymbol{\mathcal X}$의 차원을 사용한다.

만약 이들이 high dimensional일 경우, cumulative regret $R(T)$는 커질 것이다.

High dimensional에서의 문제를 다루기 위해선…

가장 자연스러운 방법은 다른 agent들이 그 환경에서 행동하면서 얻어진 abundant observational data를 활용하는 것이다.

UC-DTR은 observational distribution $P\left(\overline{\boldsymbol{s}}_{K}, \overline{\boldsymbol{x}}_{K}, y\right)$에서의 지식을 활용하지 못한다.

Observational sample들을 활용하여 online learner의 performance가 향상될 수 있도록하는 procedure를 보이겠다.

만약 $\overline{\boldsymbol{S}}_{K}$가 $\overline{\boldsymbol{X}}_{K}, Y$에 대한 sequential backdoor criterion을 만족할 때, ${P}_{\overline{\boldsymbol{x}}_{k}}\left(s_{k+1} \mid \overline{\boldsymbol{s}}_{k}\right)$와 $E_{\overline{\boldsymbol{x}}_{K}}\left[Y \mid \bar{s}_{k}\right]$는 identifiable하다.

그러면 optimal policy는 Q-learning같은 standard off-policy learning으로 구할 수 있다. See [7] Sec 3.5

하지만 위처럼 sbc가 깨지는 경우 non identifiability 문제가 발생한다.

Theorem 4 (non-identifiable할 경우)

Given $P\left(\overline{\boldsymbol{s}}_{K}, \overline{\boldsymbol{x}}_{K}, y\right)>0$, $^\exists \text{DTR } M_1, M_2$ s.t.

$P^{M_{1}}\left(\overline{\boldsymbol{s}}_{K}, \overline{\boldsymbol{x}}_{K}, y\right)= P^{M_{2}}\left(\overline{\boldsymbol{s}}_{K}, \overline{\boldsymbol{x}}_{K}, y\right)=P\left(\overline{\boldsymbol{s}}_{K}, \overline{\boldsymbol{x}}_{K}, y\right)$
but
$\begin{equation}
P_{\overline{\boldsymbol{x}}_{K}}^{M_{1}}\left(\overline{\boldsymbol{s}}_{K}, y\right) \neq P_{\overline{\boldsymbol{x}}_{K}}^{M_{2}}\left(\overline{\boldsymbol{s}}_{K}, y\right)
\end{equation}$

3.1 Bounds and Partial Identification in DTRs

${P}_{\overline{\boldsymbol{x}}_{k}}\left(s_{k+1} \mid \overline{\boldsymbol{s}}_{k}\right)$ 와 $E_{\overline{\boldsymbol{x}}_{K}}\left[Y \mid \bar{s}_{k}\right]$ 에 bound를 주는 방식으로 partially identify한다.

Lemma 1 (Causal gap이 Observational gap보다 작다.)

For a DTR with $P\left(\overline{\boldsymbol{s}}_{K}, \overline{\boldsymbol{x}}_{K}, y\right)$,

$\begin{equation} P_{\overline{\boldsymbol{x}}_{k}}\left(\overline{\boldsymbol{s}}_{k+1}\right)-P_{\overline{\boldsymbol{x}}_{k}}\left(\overline{\boldsymbol{s}}_{k}\right) \leq P\left(\overline{\boldsymbol{s}}_{k+1}, \overline{\boldsymbol{x}}_{k}\right)-P\left(\overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k}\right) \end{equation}$

Lemma 1은 transition probability의 bound를 유도하는 데 사용된다.

Theorem 5 (Transition probabilities에 대한 bound)

$\begin{equation} \frac{P\left(\overline{\boldsymbol{s}}_{k+1}, \overline{\boldsymbol{x}}_{k}\right)}{\Gamma\left(\overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k-1}\right)} \leq P_{\overline{\boldsymbol{x}}_{k}}\left(s_{k+1} \mid \overline{\boldsymbol{s}}_{k}\right) \leq \frac{\Gamma\left(\overline{\boldsymbol{s}}_{k+1}, \overline{\boldsymbol{x}}_{k}\right)}{\Gamma\left(\overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k-1}\right)} \end{equation}$

where

$\Gamma\left(\overline{\boldsymbol{s}}_{k+1}, \overline{\boldsymbol{x}}_{k}\right)=P\left(\overline{\boldsymbol{s}}_{k+1}, \overline{\boldsymbol{x}}_{k}\right)-P\left(\overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k}\right)+\Gamma\left(\overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k-1}\right)$
$\Gamma\left(s_{1}\right)=P\left(s_{1}\right)$

Theorem 5는 DTR의 functional relationship을 활용하여 bound를 제시하였고, 이는 이전에 알려진 bound [17, 3, 39] 보다 낫다.

Let $\left[a_{\overline{\boldsymbol{x}}_{k}, \overline{\boldsymbol{s}}_{k}}\left(s_{k+1}\right), b_{\overline{\boldsymbol{x}}_{k}, \overline{\boldsymbol{s}}_{k}}\left(s_{k+1}\right)\right] = \left[ \frac{P\left(\overline{\boldsymbol{s}}_{k+1}, \overline{\boldsymbol{x}}_{k}\right)}{\Gamma\left(\overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k-1}\right)},\frac{\Gamma\left(\overline{\boldsymbol{s}}_{k+1}, \overline{\boldsymbol{x}}_{k}\right)}{\Gamma\left(\overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k-1}\right)} \right]$

Theorem 6 ($\left[a_{\overline{\boldsymbol{x}}_{k}, \overline{\boldsymbol{s}}_{k}}\left(s_{k+1}\right), b_{\overline{\boldsymbol{x}}_{k}, \overline{\boldsymbol{s}}_{k}}\left(s_{k+1}\right)\right] $는 optimal bound이다.)

There exists DTRs $M_{1}, M_{2}$ s.t.

$P^{M_{1}}\left(\overline{\boldsymbol{s}}_{K}, \overline{\boldsymbol{x}}_{K}, y\right)=P^{M_{2}}\left(\overline{\boldsymbol{s}}_{K}, \overline{\boldsymbol{x}}_{K}, y\right)=P\left(\overline{\boldsymbol{s}}_{K}, \overline{\boldsymbol{x}}_{K}, y\right)$
$P_{\overline{\boldsymbol{x}}_{k}}^{M_{1}}\left(s_{k+1} \mid \overline{\boldsymbol{s}}_{k}\right)=a_{\overline{\boldsymbol{x}}_{k}, \overline{\boldsymbol{s}}_{k}}\left(s_{k+1}\right)$
$P_{\overline{\boldsymbol{x}}_{k}}^{M_{2}}\left(s_{k+1} \mid \overline{\boldsymbol{s}}_{k}\right)=b_{\overline{\boldsymbol{x}}_{k}, \overline{\boldsymbol{s}}_{k}}\left(s_{k+1}\right)$

Corollary 1

$\frac{E\left[Y \mid \bar{s}_{K}, \overline{\boldsymbol{x}}_{K}\right] P\left(\overline{\boldsymbol{s}}_{K}, \overline{\boldsymbol{x}}_{K}\right)}{\Gamma\left(\overline{\boldsymbol{s}}_{K}, \overline{\boldsymbol{x}}_{K-1}\right)} \leq E_{\overline{\boldsymbol{x}}_{K}}\left[Y \mid \bar{s}_{k}\right] \leq 1-\frac{\left(1-E\left[Y \mid \overline{\boldsymbol{s}}_{K}, \overline{\boldsymbol{x}}_{K}\right]\right) P\left(\overline{\boldsymbol{s}}_{K}, \overline{\boldsymbol{x}}_{K}\right)}{\Gamma\left(\overline{\boldsymbol{s}}_{K}, \overline{\boldsymbol{x}}_{K-1}\right)}$

3.2 The Causal UC-DTR Algorithm

UC-DTR의 성능을 올리기 위해, Theorem 5와 Corollary 1에서 구한 bound를 활용하는 방법을 도입하겠다.

For $k=1, …, K-1$,

$\begin{aligned} \boldsymbol{\mathcal{C}}_{k}&=\left\{P :P_{\overline{\boldsymbol{x}}_{k}}\left(s_{k+1} \mid \overline{\boldsymbol{s}}_{k}\right) \in\left[a_{\overline{\boldsymbol{x}}_{k}, \overline{\boldsymbol{s}}_{k}}\left(s_{k+1}\right), b_{\overline{\boldsymbol{x}}_{k}, \overline{\boldsymbol{s}}_{k}}\left(s_{k+1}\right)\right] ;\quad \forall (\bar{s}_{k+1}, \overline{\boldsymbol{x}}_{k})\right\} \\ \\ \boldsymbol{\mathcal{C}}_{K}&=\left\{ \mathbb E :\mathbb E_{\overline{\boldsymbol{x}}_{K}}\left[Y \mid \overline{\boldsymbol{s}}_{K}\right] \in\left[a_{\overline{\boldsymbol{x}}_{K}, \overline{\boldsymbol{s}}_{K}}, b_{\overline{\boldsymbol{x}}_{K}, \overline{\boldsymbol{s}}_{K}}\right] ;\quad \forall (\bar{s}_{k+1}, \overline{\boldsymbol{x}}_{k})\right\} \end{aligned}$

$\boldsymbol{\mathcal C} = \{ \boldsymbol{\mathcal C}_1, \boldsymbol{\mathcal C}_2, \cdots, \boldsymbol{\mathcal C}_K\}$ 를 causal bounds 라고 하자.

$\text {UC}^{c} \text { -DTR }$은 UC-DTR의 변형으로 possible DTR set에 causal bound를 만족해야 한다는 조건을 추가한다.

그래서 Linear programming 부분에 constraint를 추가하는 방식으로 풀 수 있다.

Let $\left|\boldsymbol{\mathcal{C}}_{k}\right|_{1}=\max _{\overline{\boldsymbol{x}}_{k}, \overline{\boldsymbol{s}}_{k}} \sum_{s_{k+1}}\left|a_{\overline{\boldsymbol{x}}_{k}, \overline{\boldsymbol{s}}_{k}}\left(s_{k+1}\right)-b_{\overline{\boldsymbol{x}}_{k}, \overline{\boldsymbol{s}}_{k}}\left(s_{k+1}\right)\right|$

Let $\left|\boldsymbol{\mathcal{C}}_{K}\right|_{1}=\max _{\overline{\boldsymbol{x}}_{K}, \overline{\boldsymbol{s}}_{K}}\left|a_{\overline{\boldsymbol{x}}_{K}, \overline{\boldsymbol{s}}_{K}}-b_{\overline{\boldsymbol{x}}_{K}, \overline{\boldsymbol{s}}_{K}}\right|$

Let $|\boldsymbol{\mathcal{C}}|_{1}=\sum_{k=1}^{K}\left|\boldsymbol{\mathcal{C}}_{k}\right|_{1}$

Theorem 7

The regret of $\text {UC}^{c} \text { -DTR }$ is bounded by w/ probability $\geq 1-\delta$

$R(T) \leq \min \left\{12 K \sqrt{|\boldsymbol{\mathcal{S}}||\boldsymbol{\mathcal{X}}| T \log (2 K|\boldsymbol{\mathcal{S}} \| \boldsymbol{\mathcal{X}}| T / \delta)},\|\boldsymbol{\mathcal{C}}\|_{1} T\right\}+4 K \sqrt{T \log (2 T / \delta)}$

만약 $T<12^{2}\left|\boldsymbol{\mathcal{S}}|\boldsymbol{\mathcal{X}} | \log (2 K|\boldsymbol{\mathcal{S}} | \boldsymbol{\mathcal{X}}| T / \delta) /| \boldsymbol{\mathcal{C}} |_{1}^{2}\right.$ 이면, UC-DTR보다 작은 bound이다.
$|\boldsymbol{\mathcal{C}}|_{1}$이 작을 수록 더 정보가 있다는 것이니, 더 나은 $T$도 더 크다는 걸 확인할 수 있다.

Theorem 8

The expected regret of $\text {UC}^{c} \text { -DTR }$ with parameter $\delta=\frac{1}{T}$ is bounded by

$E[R(T)] \leq \max _{\boldsymbol{\pi} \in \Pi_{\boldsymbol{\mathcal{c}}}^{-}}\left\{\frac{33^{2} K^{2}| \boldsymbol{\mathcal{S}} \| \boldsymbol{\mathcal{X}}| \log (T)}{\Delta_{\pi}}+\frac{32}{\Delta_{\pi}^{3}}+\frac{4}{\Delta_{\pi}}\right\}+1$

$\mathbf{\Pi}_{\boldsymbol{C}}^{-} \subseteq \mathbf{\Pi}^{-}$ 이므로, UC-DTR보다 작은 bound이다.

4 Experiments

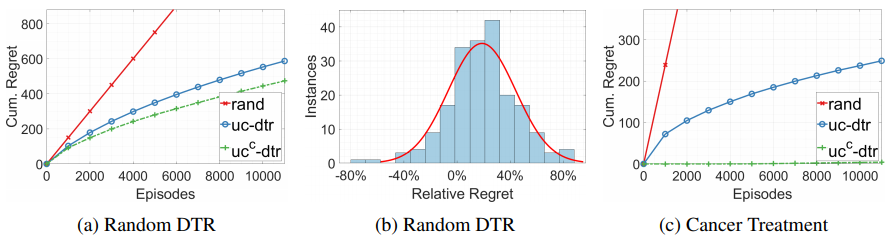
(c)는 Cancer and Leukemia Group B에서 실행된 two-stage clinical trial이다.

Appendix 1

A.1.1 Proof of Theorems 1 to 3

Let “an episode $t$ is $\epsilon$-bad” if $V_{\boldsymbol{\pi}^{\star}}\left(M^{\star}\right)-Y^t \geq \epsilon$

Let $T_\epsilon$ be the number of $\epsilon$-bad episodes in UC_DTR

Let $L_{\epsilon}$ be the indicies of the $\epsilon$-bad episodes up to $T$

Let $R_{\epsilon}(T)=\sum_{t \in L_{f}} V_{\pi^{\star}}\left(M^{\star}\right)-Y^{t}$

Let $N\left(\overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k}\right)=\sum_{t=1}^{T} I_{\overline{\boldsymbol{S}}_{k}^{t}=\overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{X}}_{k}^{t}=\overline{\boldsymbol{x}}_{k}}$

Let $\mathcal{H}^{t}=\left\{\overline{\boldsymbol{X}}_{K}^{1}, \overline{\boldsymbol{S}}_{K}^{1}, Y^{1}, \ldots, \overline{\boldsymbol{X}}_{K}^{t}, \overline{\boldsymbol{S}}_{K}^{t}, Y^{t}\right\}$

Lemma 2

Fix $\epsilon \in (0, 1)$. Then,

$\sum_{t \in L_{e}}\left(E_{\bar{X}_{K}^{t}}\left[Y \mid \overline{\boldsymbol{S}}_{K}^{t}\right]-Y^{t}\right) \leq \sqrt{\frac{T_{\epsilon} \log (1 / \delta)}{2}} \quad \text{w/ pbt $\geq 1-\delta$}$

(Proof)

Let $\boldsymbol{D}^{T} = \left\{\overline{\boldsymbol{X}}_{K}^{1}, \overline{\boldsymbol{S}}_{K}^{1}, \ldots, \overline{\boldsymbol{X}}_{K}^{T}, \overline{\boldsymbol{S}}_{K}^{T}\right\}$

Since $Y^t \in (0, 1)$ and $Y^t$ are conditionally independent, by applying Hoeffding’s inequality

$\begin{aligned} &P\left(\sum_{t \in L_{e}}\left(E_{\overline{\boldsymbol{x}}_{K}^{t}}\left[Y \mid \overline{\boldsymbol{s}}_{K}^{t}\right]-Y^{t}\right) \geq \sqrt{\frac{T_{\epsilon} \log (1 / \delta)}{2}} \mid \boldsymbol{d}^{T}\right) \\ =&P\left(\frac{1}{T_\epsilon}\sum_{t \in L_{e}}\left(E_{\overline{\boldsymbol{x}}_{K}^{t}}\left[Y \mid \overline{\boldsymbol{s}}_{K}^{t}\right]-Y^{t}\right) \geq \sqrt{\frac{\log (1 / \delta)}{2T_{\epsilon} }} \mid \boldsymbol{d}^{T}\right) \leq \exp(-2 T_{\epsilon} \frac{\log (1 / \delta)}{2T_{\epsilon} } / (1-0)^2) =\delta \end{aligned}$

Therefore,

$\begin{aligned} P\left(\sum_{t \in L_{e}}\left(E_{\overline{\boldsymbol{X}}_{K}^{t}}\left[Y \mid \overline{\boldsymbol{S}}_{K}^{t}\right]-Y^{t}\right) \geq \sqrt{\frac{T_{\epsilon} \log (1 / \delta)}{2}} \right) =& \\ \sum_{\boldsymbol d^T} P\left(\sum_{t \in L_{e}}\left(E_{\overline{\boldsymbol{X}}_{K}^{t}}\left[Y \mid \overline{\boldsymbol{S}}_{K}^{t}\right]-Y^{t}\right) \geq \sqrt{\frac{T_{\epsilon} \log (1 / \delta)}{2}} \mid \boldsymbol d^T \right) P(\boldsymbol d^T) \leq & \\ \sum_{\boldsymbol d^T} \delta P(\boldsymbol d^T) = \delta& \end{aligned}$

Lemma 3

Fix $\epsilon > 0$. Then w/ pbt $\geq 1-\delta$

$^{\forall}T > 1, \quad R_{\epsilon}(T) \leq 12 K \sqrt{|\mathcal{S} \| \mathcal{X}| T_{\epsilon} \log (2 K|\mathcal{S} \| \mathcal{X}| T / \delta)}+4 K \sqrt{T_{\epsilon} \log (2 T / \delta)}$

(Proof)

Let $M^{\star}$ denote the underlying DTR.

$\mathcal M_t$ is a set of DTR instances s.t. for any $M \in \mathcal M_t$, its system dynamics satisfy

$\left|P_{\overline{\boldsymbol{x}}_{k}}^{M}\left(\cdot \mid \bar{s}_{k}\right)-\hat{P}_{\overline{\boldsymbol{x}}_{k}}^{t}\left(\cdot \mid \bar{s}_{k}\right)\right|_{1} \leq \sqrt{\frac{6\left|\mathcal{S}_{k+1}\right| \log \left(2 K\left|\overline{\boldsymbol{\mathcal { S }}}_{k}\right|\left|\overline{\boldsymbol{\mathcal { X }}}_{k}\right| t / \delta\right)}{\max \left\{1, N^{t}\left(\bar{s}_{k}, \overline{\boldsymbol{x}}_{k}\right)\right\}}}$
$\left|E_{\overline{\boldsymbol{x}}_{K}}^{M}\left[Y \mid \overline{\boldsymbol{s}}_{K}\right]-\hat{E}_{\overline{\boldsymbol{x}}_{K}}^{t}\left[Y \mid \overline{\boldsymbol{s}}_{K}\right]\right| \leq \sqrt{\frac{2 \log (2 K|\mathcal{S} | \mathcal{X}| t / \delta)}{\max \left\{1, N^{t}\left(\overline{\boldsymbol{s}}_{K}, \overline{\boldsymbol{x}}_{K}\right)\right\}}}$

UCRL2, Appendix C.1에서,

$\varepsilon=\sqrt{\frac{2}{n} \log \left(\frac{2^{S} 20 S A t^{7}}{\delta}\right)} \leq \sqrt{\frac{14 S}{n} \log \left(\frac{2 A t}{\delta}\right)} \quad \text{and} \quad \varepsilon_{r}=\sqrt{\frac{1}{2 n} \log \left(\frac{120 S A t}{\delta}\right)} \leq \sqrt{\frac{7}{2 n} \log \left(\frac{2 S A t}{\delta}\right)}$
$\varepsilon=\sqrt{\frac{2 }{n} \log \left( \frac{2^{\left|\mathcal{S}_{k+1}\right|} 8K\left|\overline{\mathcal{S}}_{k}\right|\left|\overline{\mathcal{X}}_{k}\right| t^3} {\delta}\right)} \leq \sqrt{\frac{6 \mathcal S_{k+1}}{n} \log \left(\frac{2K\left|\overline{\mathcal{S}}_{k}\right|\left|\overline{\mathcal{X}}_{k}\right| t}{\delta}\right)} \quad \text{and} \quad \varepsilon_{r}=\sqrt{\frac{1}{2 n} \log \left(\frac{8 K^2 |\mathcal S| |\mathcal X| t^3}{\delta}\right)} \leq \sqrt{\frac{2}{n} \log \left(\frac{2K |\mathcal S| |\mathcal X| t}{\delta}\right)}$
로 바꾸면 $P\left(M^{\star} \notin \mathcal{M}_{t}\right) \leq \frac{\delta}{4 t^{2}}$
- (노테이션이 달라서 실수로 $t$를 timestep으로 착각하고 유도했었는데 비슷할 듯)
모든 episode에서 $M^\star \in \mathcal M_t$일 확률은 $1-\frac{\delta}{2}$보다 크다.
$\begin{aligned} P \left ( \cap_{t=1} ^\infty \left\{ M^\star\in \mathcal M_t \right\}\right) &= 1 - P \left ( \cup_{t=1} ^\infty \left\{ M^\star \not\in \mathcal M_t \right\}\right) \\ &\geq 1 - \sum_{t=1}^\infty P \left (\left\{ M^\star \not\in \mathcal M_t \right\}\right) \\ &\geq 1 - \sum_{t=1}^\infty\frac{\delta}{4t^2} \\ &\geq 1 - \frac{\delta}{2} \quad \because \sum_{t=1}^{\infty} \frac{1}{4 t^{2}} \leq \frac{\pi^{2}}{24} \delta<\frac{\delta}{2} \end{aligned}$
$\frac{\delta}{2}$만큼의 확률은 내주고 아래의 증명에서 모든 episode에서 $M^\star \in \mathcal M_t$인 경우만 고려하겠다.
$\begin{aligned} R_{\epsilon}(T) &=\sum_{t \in L_{f}} V_{\pi^{\star}}\left(M^{\star}\right)-Y^{t} \\ =& \sum_{t \in L_{\epsilon}}\left(V_{\pi^{\star}}\left(M^{\star}\right)-E_{\overline{\boldsymbol{X}}_{K}^{t}}^{M_{t}}\left[Y \mid \overline{\boldsymbol{S}}_{K}^{t}\right]\right) &(19) \\ &+\sum_{t \in L_{\epsilon}}\left(E_{\overline{\boldsymbol{X}}_{K}^{t}}^{M_{t}}\left[Y \mid \overline{\boldsymbol{S}}_{K}^{t}\right]-E_{\overline{\boldsymbol{X}}_{K}^{t}}\left[Y \mid \overline{\boldsymbol{S}}_{K}^{t}\right]\right) &(20) \\ &+\sum_{t \in L_{\epsilon}}\left(E_{\overline{\boldsymbol{X}}_{K}^{t}}\left[Y \mid \bar{S}_{K}^{t}\right]-Y^{t}\right)&(21) \end{aligned}$
Bounding Eq. (19)
- Let $V_{\boldsymbol{\pi}}\left(\overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k-1} ; M\right)=E_{\boldsymbol{\pi}}^{M}\left[Y \mid \overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k-1}\right]$
- Let $V_{\boldsymbol{\pi}}\left(\overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k} ; M\right)=E_{\boldsymbol{\pi}}^{M}\left[Y \mid \overline{\boldsymbol{s}}_{k}, \overline{\boldsymbol{x}}_{k}\right]$
- Since $M^{\star} \in \mathcal{M}_{t}$, $\quad V_{\boldsymbol{\pi}^{}}\left(s_{1} ; M^{}\right) \leq V_{\boldsymbol{\pi}_{t}}\left(s_{1} ; M_{t}\right)$
- Since $\pi_{t}$ is deterministic, $\quad V_{\boldsymbol{\pi}_{t}}\left(\overline{\boldsymbol{S}}_{k}^{t}, \overline{\boldsymbol{X}}_{k-1}^{t} ; M\right)=V_{\boldsymbol{\pi}_{t}}\left(\overline{\boldsymbol{S}}_{k}^{t}, \overline{\boldsymbol{X}}_{k}^{t} ; M\right)$
- Thus, we have

Let $M_{t}(k)$ denote a combined DTR from $M^{\star}$ and $M_t$ s.t.

$\begin{aligned} P_{\overline{\boldsymbol{x}}_{i}}^{M_{t}(k)}\left(s_{i+1} \mid \overline{\boldsymbol{s}}_{i}\right)& = P_{\overline{\boldsymbol{x}}_{i}}\left(s_{i+1} \mid \bar{s}_{i}\right) \quad \text{for $i=0, 1, \ldots, k-1$} \\ P_{\overline{\boldsymbol{x}}_{i}}^{M_{t}(k)}\left(s_{i+1} \mid \overline{\boldsymbol{s}}_{i}\right) &= P^{M_t}_{\overline{\boldsymbol{x}}_{i}}\left(s_{i+1} \mid \bar{s}_{i}\right) \quad \text{for $i=k, k+1, \ldots, K-1$} \end{aligned}$

Then,
- $P_{\boldsymbol{\pi}}^{M_{t}(k)}\left(\overline{\boldsymbol{x}}_{K}, \overline{\boldsymbol{s}}_{K}, y\right)=P_{\overline{\boldsymbol{x}}_{K}}^{M_{t}}\left(y \mid \overline{\boldsymbol{s}}_{K}\right) \prod_{i=0}^{k-1} P_{\overline{\boldsymbol{x}}_{i}}\left(s_{i+1} \mid \overline{\boldsymbol{s}}_{i}\right) \prod_{j=k}^{K-1} P_{\overline{\boldsymbol{x}}_{j}}^{M_{t}}\left(s_{i+1} \mid \overline{\boldsymbol{s}}_{j}\right) \prod_{l=1}^{K-1} \pi_{l+1}\left(x_{l+1} \mid \overline{\boldsymbol{s}}_{l+1}, \overline{\boldsymbol{x}}_{l}\right)$
- $\begin{aligned} &V_{\pi_{t}}\left(\bar{\boldsymbol S}_{k}^{t}, \overline{\boldsymbol{X}}_{k}^{t} ; M_{t}^{(k)}\right)-V_{\pi_{t}}\left(\bar{\boldsymbol S}_{k}^{t}, \overline{\boldsymbol{X}}_{k}^{t} ; M_{t}^{(k+1)}\right) \\ &=\sum_{s_{k+1}}\left(P^{M_{t}}\left(s_{k+1} \mid \bar{\boldsymbol S}_{k}, \overline{\boldsymbol{X}}_{k}\right)-P\left(s_{k+1} \mid \bar{\boldsymbol S}_{k}, \overline{\boldsymbol{X}}_{k}\right)\right) V_{\pi_{t}}\left(s_{k+1}, \bar{\boldsymbol S}_{k}^{t}, \overline{\boldsymbol{X}}_{k}^{t} ; M_{t}\right) \\ &\leq\left\|P_{\overline{\boldsymbol{x}}_{k}}^{M_{t}}\left(\mid \bar{\boldsymbol s}_{k}\right)-P_{\overline{\boldsymbol{x}}_{k}}\left(\cdot \mid \bar{\boldsymbol s}_{k}\right)\right\| \max _{s_{k+1}} v_{k+1}\left(s_{k+1}, \overline{\boldsymbol{S}}_{k}^{t}, \overline{\boldsymbol{X}}_{k}^{t} ; M_{t}\right) \\ &\leq 2 \sqrt{6\left|\mathcal{S}_{k+1}\right| \log \left(2 K\left|\overline{\boldsymbol {\mathcal{S}}}_{k}\right|\left|\overline{\boldsymbol {\mathcal{X}}}_{k}\right| T / \delta\right)} \frac{1}{\sqrt{\max \left\{1, N^{t}\left(\overline{\boldsymbol{S}}_{k}^{t}, \overline{\boldsymbol{X}}_{k}^{t}\right)\right.}} \end{aligned}$
- $\sum_{t \in L_{\epsilon}} \frac{1}{\sqrt{\max \left\{1, N^{t}\left(\overline{\boldsymbol{S}}_{k}^{t}, \overline{\boldsymbol{X}}_{k}^{t}\right)\right\}}} \leq(\sqrt{2}+1) \sqrt{T_{\epsilon}\left|\overline{\boldsymbol{\mathcal { S }}}_{k}\right|\left|\overline{\boldsymbol{\mathcal { X }}}_{k}\right|} \qquad \text{in UCRL2, appendix D}$
$\begin{aligned} &\sum_{t \in L_{\epsilon}} \sum_{k=1}^{K-1} V_{\boldsymbol{\pi}_{t}}\left(\overline{\boldsymbol{S}}_{k}^{t}, \overline{\boldsymbol{X}}_{k}^{t} ; M_{t}^{(k)}\right)-V_{\boldsymbol{\pi}_{t}}\left(\overline{\boldsymbol{S}}_{k}^{t}, \overline{\boldsymbol{X}}_{k}^{t} ; M_{t}^{(k+1)}\right) \\ &\leq \sum_{k=1}^{K-1} 2(\sqrt{2}+1) \sqrt{6 T_{\epsilon}\left|\overline{\boldsymbol{\mathcal{S}}}_{k+1}\right|\left|\overline{\boldsymbol{\mathcal { X }}}_{k}\right| \log \left(2 K\left|\overline{\boldsymbol{\mathcal { S }}}_{k}\right|\left|\overline{\boldsymbol{\mathcal { X }}}_{k}\right| T / \delta\right)} \\ &\leq 2(\sqrt{2}+1)(K-1) \sqrt{6 T_{\epsilon}|\boldsymbol{\mathcal{S}} \| \boldsymbol{\mathcal{X}}| \log (2 K|\boldsymbol {\mathcal{S}} \| \boldsymbol{\mathcal{X}}| T / \delta)} & (24) \end{aligned}$
Since $E \left [\left|Z_{t}\right| \right] \leq K$ and $E\left[Z_{t+1} \mid \mathcal{H}_{t}\right]=0$,
- $Z_t$ is a martingale difference sequence w.r.t. $\{ \overline{\boldsymbol{X}}_{K}^{t}, \overline{\boldsymbol{S}}_{K}^{t}, Y^{t}\}_{t=1, 2, \ldots}$
$\begin{aligned} P\left(\sum_{t \in L_{\epsilon}} Z_{t} \leq K \sqrt{6 T_{\epsilon} \log (2 T / \delta)} \right) & \geq 1- \exp\left( -\frac{2K^2 6T_{\epsilon} \log \left( 2T / \delta\right)}{T_\epsilon (2K)^2}\right) & \because \text{Azuma-Hoeffding inequality} \\ &= 1 - \frac{\delta^3}{8T^3} \\ & \geq 1 - \frac{\delta}{8T^2} &\because \delta^2 \leq T \end{aligned}$
Since $\sum_{T=1}^{\infty} \frac{\delta}{8 T^{2}} \leq \frac{\pi^{2}}{48} \delta<\frac{\delta}{4}$,
- $P\left(\sum_{t \in L_{\epsilon}} Z_{t} \leq K \sqrt{6 T_{\epsilon} \log (2 T / \delta)} \right) \geq 1-\frac{\delta}{4} \quad \text{for all }T \quad (25)$
Eqs. (24) and (25) combined give
- $\begin{aligned} &\sum_{t \in L_{\epsilon}}\left(V_{\boldsymbol{\pi}^{*}}\left(M^{*}\right)-E_{\overline{\boldsymbol{X}}_{K}^{t}}^{M_{t}}\left[Y \mid \overline{\boldsymbol{S}}_{K}^{t}\right]\right) \\ &\leq 2(\sqrt{2}+1)(K-1) \sqrt{6 T_{\epsilon}|\boldsymbol{\mathcal{S}} \| \boldsymbol{\mathcal{X}}| \log (2 K|\boldsymbol {\mathcal{S}} \| \boldsymbol{\mathcal{X}}| T / \delta)}+K \sqrt{6 T_{\epsilon} \log (2 T / \delta)} \end{aligned}$

Bounding Eq. (20)
- $\begin{aligned} E_{\overline{\boldsymbol{X}}_{K}^{t}}^{M_{t}}\left[Y \mid \overline{\boldsymbol{S}}_{K}^{t}\right]-E_{\overline{\boldsymbol{X}}_{K}^{t}}\left[Y \mid \overline{\boldsymbol{S}}_{K}^{t}\right] &\leq \left|E_{\overline{\boldsymbol{x}}_{K}}^{M_{t}}\left[Y \mid \overline{\boldsymbol{S}}_{K}^{t}\right]-\hat{E}_{\overline{\boldsymbol{x}}_{K}}^{t}\left[Y \mid \overline{\boldsymbol{S}}_{K}^{t}\right]\right|+\left|E_{\overline{\boldsymbol{X}}_{K}^{t}}\left[Y \mid \overline{\boldsymbol{S}}_{K}^{t}\right]-\hat{E}_{\overline{\boldsymbol{x}}_{K}}^{t}\left[Y \mid \overline{\boldsymbol{S}}_{K}^{t}\right]\right| \\ &\leq 2 \sqrt{2 \log (2 K|\boldsymbol{\mathcal{S}} \| \boldsymbol{\mathcal{X}}| T / \delta)} \frac{1}{\sqrt{\max \left\{1, N^{t}\left(\overline{\boldsymbol{S}}_{K}^{t}, \overline{\boldsymbol{X}}_{K}^{t}\right)\right\}}} \\ \\ & \leq 2(\sqrt{2}+1) \sqrt{2 T_{\epsilon}|\mathcal{S} \| \mathcal{X}| \log (2 K|\mathcal{S} \| \mathcal{X}| T / \delta)} \\ & \because \text{UCRL2 appendix D} \sum_{t \in L_{\epsilon}} \frac{1}{\sqrt{\max \left\{1, N^{t}\left(\overline{\boldsymbol{S}}_{K}^{t}, \overline{\boldsymbol{X}}_{K}^{t}\right)\right\}}} \leq(\sqrt{2}+1) \sqrt{T_{\epsilon}|\boldsymbol{\mathcal{S}} \| \boldsymbol{\mathcal{X}}|} \end{aligned}$
Bounding Eq. (21)
- Lemma 2에서 $\sqrt{\frac{T_{\epsilon} \log (1 / \delta)}{2}} $ 대신에 $\sqrt{\frac{3 T_{\epsilon} \log (2 T / \delta)}{2}}$를 대입하면,
  - $\sum_{t \in L_{\epsilon}}\left(E_{\overline{\boldsymbol{X}}_{K}^{t}}\left[Y \mid \overline{\boldsymbol{S}}_{K}^{t}\right]-Y^{t}\right) \leq \sqrt{\frac{3 T_{\epsilon} \log (2 T / \delta)}{2}} \quad \text{w/ pbt }\geq 1- \exp\left( -2T_{\epsilon}\frac{3 \log (2 T / \delta)}{2 T_{\epsilon}}\right)\geq 1-\frac{\delta}{8T^2}$
- Since $\sum_{T=1}^{\infty} \frac{\delta}{8 T^{2}} \leq \frac{\pi^{2}}{48} \delta<\frac{\delta}{4}$,
  - $\sum_{t \in L_{\epsilon}}\left(E_{\overline{\boldsymbol{X}}_{K}^{t}}\left[Y \mid \overline{\boldsymbol{S}}_{K}^{t}\right]-Y^{t}\right) \leq \sqrt{\frac{3 T_{\epsilon} \log (2 T / \delta)}{2}} \quad \text{w/ pbt }\geq 1 -\frac{\delta}{4}$
Hence,
- $\begin{aligned}
  R_{\epsilon}(T) & \leq 2(\sqrt{2}+1)(K-1) \sqrt{6 T_{\epsilon}|\boldsymbol{\mathcal{S}} | \boldsymbol{\mathcal{X}}| \log (2 K|\boldsymbol {\mathcal{S}} | \boldsymbol{\mathcal{X}}| T / \delta)}+K \sqrt{6 T_{\epsilon} \log (2 T / \delta)} \\ &+ 2(\sqrt{2}+1) \sqrt{2 T_{\epsilon}|\mathcal{S} | \mathcal{X}| \log (2 K|\mathcal{S} | \mathcal{X}| T / \delta)} + \sqrt{\frac{3 T_{\epsilon} \log (2 T / \delta)}{2}} \quad \text{w/ pbt}\geq 1-\frac{\delta}{2}-\frac{\delta}{4}-\frac{\delta}{4}=1-\delta \\ &\leq 12 K \sqrt{|\mathcal{S}||\mathcal{X}| T_{\epsilon} \log (2 K|\mathcal{S} | \mathcal{X}| T / \delta)}+4 K \sqrt{T_{\epsilon} \log (2 T / \delta)} \quad \text{: Simplification}
  \end{aligned}$

Theorem 1 (Upper bound)

The regret of UC-DTR is bounded by w/ probability $\geq 1-\delta$

$R(T) \leq12 K \sqrt{| \boldsymbol{\mathcal{S}}|| \boldsymbol{\mathcal{X}}| T \log (2 K|\boldsymbol{\mathcal{S}} \| \boldsymbol{\mathcal{X}}| T / \delta)}+4 K \sqrt{T \log (2 T / \delta)}$

(Proof)

Fix $\epsilon = 0$

Then, $T_{\epsilon} = T$ and $R_{\epsilon}(T) = R(T)$

By Lemma 3,

$\begin{aligned} R(T) \leq 12 K \sqrt{|\mathcal{S}||\mathcal{X}| T \log (2 K|\mathcal{S} \| \mathcal{X}| T / \delta)}+4 K \sqrt{T \log (2 T / \delta)} \quad \text{: Simplification} \end{aligned}$

Theorem 2 (Gap-dependent upper bound)

Let $\mathbf{\Pi}^{-}$ denote the set of sub-optimal policies $\left\{\boldsymbol{\pi} \in \boldsymbol{\Pi}: V_{\boldsymbol{\pi}}\left(M^{\star}\right)<V_{\boldsymbol{\pi}^{\star}}\left(M^{\star}\right)\right\}$

Let $\Delta_{\boldsymbol{\pi}}=V_{\boldsymbol{\pi}^{\star}}\left(M^{\star}\right)-V_{\boldsymbol{\pi}}\left(M^{\star}\right)$

Then, the expected regret of UC-DTR with parameter $\delta=\frac{1}{T}$ is bounded by

(Proof)

By Lemma 3,

$R_{\epsilon}(T) \leq 23 K \sqrt{|\boldsymbol{\mathcal{S}}||\boldsymbol{\mathcal{X}}| T_{\epsilon} \log (T / \delta)} \qquad \text{(w/ pbt $\geq 1-\delta$)}$

Since $R_{\epsilon}(T) \geq \epsilon T_{\epsilon}$,

$T_{\epsilon} \leq \frac{23^{2} K^{2}|\boldsymbol{\mathcal{S}} \| \boldsymbol{\mathcal{X}}| \log (T / \delta)}{\epsilon^{2}} \qquad \text{(w/ pbt $\geq 1-\delta$)}$

Therefore,

$R_{\epsilon}(T) \leq \frac{23^{2} K^{2}| \boldsymbol{\mathcal{S}} \| \boldsymbol{\mathcal{X}}| \log (T / \delta)}{\epsilon} \qquad \text{(w/ pbt $\geq 1-\delta$)}$

Let $\Delta = \arg \min _{\boldsymbol{\pi} \in \boldsymbol{\Pi}^{-}} \Delta_{\boldsymbol{\pi}}$

Let $\epsilon=\frac{\Delta}{2}$

Let $\delta=\frac{1}{T}$

Then,

$\begin{aligned} E\left[R_{\frac{\Delta}{2}}(T)\right] & \leq \frac{23^{2} K^{2}|\boldsymbol{\mathcal{S}} \| \boldsymbol{\mathcal{X}}| \log (T / \frac{1}{T})}{\frac{\Delta}{2}} \left(1- \delta\right) + T \delta & \because R(T) \leq T \\ &\leq \frac{46^{2} K^{2}| \boldsymbol{\mathcal{S}} \| \boldsymbol{\mathcal{X}}| \log (T)}{\Delta}+1 \end{aligned}$

논문에선 $33^2$이라고 했는데 어떻게 derive 된 것?

$\epsilon$-good episode들도 고려해보자.

Let $\tilde{R}_{\epsilon}(T)$ denote the regret in $\epsilon$-good episodes.

Let $\tilde T_{\epsilon}$ be the total number of $\epsilon$-good episodes.

Let $\tilde L_{\epsilon}$ be the indices of $\epsilon$-good episodes.

Consider the event $\{\tilde{T}_{\frac{\Delta}{2}}=t \}$

Then, $\{\tilde{T}_{\frac{\Delta}{2}}=t \}$ implies

$\begin{aligned} \tilde{R}_{\epsilon}(T)=\sum_{i \in \tilde{L}_{\frac{\Delta}{2}}} V_{\boldsymbol{\pi}^{*}}\left(M^{*}\right)-Y^{i} &\leq t \frac{\Delta}{2} \\ &\Leftrightarrow \\ \sum_{i \in \tilde{L}_{\frac{\Delta}{2}}} V_{\boldsymbol{\pi}^{*}}\left(M^{*}\right)-V_{\boldsymbol{\pi}_{i}}\left(M^{*}\right)-Y^{i} &\leq t \frac{\Delta}{2}-\sum_{i \in \tilde{L}_{\frac{\Delta}{2}}} V_{\boldsymbol{\pi}_{i}}\left(M^{*}\right) \\ &\Leftrightarrow \\ \sum_{i \in \tilde{L}_{\frac{\Delta}{2}}} \Delta_{\boldsymbol{\pi}_{i}}-Y^{i} &\leq t \frac{\Delta}{2}-\sum_{i \in \tilde{L}_{\frac{\Delta}{2}}} V_{\boldsymbol{\pi}_{i}}\left(M^{*}\right) \\ &\Rightarrow \\ \sum_{i \in \tilde{L}_{\frac{\Delta}{2}}} \Delta-Y^{i} &\leq t \frac{\Delta}{2}-\sum_{i \in \tilde{L}_{\frac{\Delta}{2}}} V_{\boldsymbol{\pi}_{i}}\left(M^{*}\right) \\ &\Leftrightarrow \\ \sum_{i \in \tilde{L}_{\frac{\Delta}{2}}} V_{\boldsymbol{\pi}_{i}}\left(M^{*}\right)-Y^{i} &\leq-t \frac{\Delta}{2} \end{aligned}$

Therefore,

$\begin{aligned} E\left[\tilde{R}_{\frac{\Delta}{2}}(T)\right] &\leq \frac{\Delta}{2} E\left[\tilde{T}_{\frac{\Delta}{2}}(T)\right] \leq \frac{\Delta}{2} \sum_{t=1}^{T} t P\left(\tilde{T}_{\frac{\Delta}{2}}=t\right) \\ &\leq \frac{\Delta}{2} \sum_{t=1}^{T} t P\left(\sum_{i \in \tilde{L}_{\frac{\Delta}{2}}} V_{\boldsymbol{\pi}_{i}}\left(M^{*}\right)-Y^{i} \leq-t \frac{\Delta}{2}\right) \\ &= \frac{\Delta}{2} \sum_{t=1}^{T} t P\left(\sum_{i \in \tilde{L}_{\frac{\Delta}{2}}} C_i \leq-t \frac{\Delta}{2}\right) &\text{where $C_{i}=V_{\boldsymbol{\pi}_{i}}\left(M^{*}\right)-Y^{t}$} \\ &\leq \frac{\Delta}{2} \sum_{t=1}^{T} te^{-\frac{\Delta^{2} t}{8}} &\text{$\left|C_{t}\right|<1$, $E\left[C_{t+1} \mid \mathcal{H}^{t}\right]=0$, Azuma-Hoeffding } \\ &\leq \frac{\Delta}{2} \frac{64}{\Delta^{4}}\left(\frac{\Delta^{2}}{8}+1\right) e^{-\frac{\Delta^{2}}{8}} &\text{I don't know} \\ & \leq \frac{32}{\Delta^{3}}+\frac{4}{\Delta} \end{aligned}$

마지막에서 두번째 부등식은 유도하지 못했다.

Hence,

$\begin{aligned} E[R(T)]&=E\left[R_{\frac{\Delta}{2}}(T)\right]+E\left[\tilde{R}_{\frac{\Delta}{2}}(T)\right] \\ &\leq \frac{33^{2} K^{2}|\mathcal{S} \| \mathcal{X}| \log (T)}{\Delta}+\frac{32}{\Delta^{3}}+\frac{4}{\Delta}+1 \end{aligned}$

Theorem 3 (Lower bound)

For any algorithm, there is a DTR $M$ with horizon $K$ s.t.

$E[R(T)] \geq 0.05 \sqrt{|\mathcal{S} \| \mathcal{X}| T} \quad \text{where $T\geq|\boldsymbol{\mathcal{S}} \| \boldsymbol{\mathcal{X}}|$}$

(Proof)

P. Auer, 2002를 보고 다시 증명해보겠다.

A.1.2 Proofs of Theorems 4 to 6, Lemma 1, and Corollary 2

이번 섹션에서, DTR의 transition probaility의 bound에 대한 증명을 하겠다.

증명은 Pearl의 counterfactual variable와 axioms of composition, effectiveness, and reversibility에 기반한다.

$Y_{\boldsymbol{x}}(\boldsymbol{u})$은 potential outcome of $Y$ to intervention $do(\boldsymbol{x})$에서 situation $\boldsymbol U = \boldsymbol u$일 때의 해이다.

Exogenous variable과 CF variable이 대응되므로 CF를 exogenous로 갖는 DTR을 생각해보자.

아래첨자 2단으로 사용하면 수식 변환이 안되어서 작성 중단

Study Repo

Near-Optimal Reinforcement Learning in Dynamic Treatment Regimes

0. Abstract

1. Introduction

1.1 Preliminaries

2. Optimizing Dynamic Treatment Regimes

2.1 The UC-DTR Algorithm

2.1.1 Finding Optimistic DTRs

2.2 Theoretical Analysis

3. Learning from Confounded Observations

3.1 Bounds and Partial Identification in DTRs

3.2 The Causal UC-DTR Algorithm

4 Experiments

Appendix 1

A.1.1 Proof of Theorems 1 to 3

A.1.2 Proofs of Theorems 4 to 6, Lemma 1, and Corollary 2