On the Identification of Causal Effects

0. Abstract

이 논문은 non experimental data로 부터, action과 policy의 effect를 estimate한다.

이 논문은 다음을 제공한다.

• causal effect(CE) identifiability(I)의 sufficient criterion
• I일 때, 이에 대한 compuation procedure

General Identification Condition for Causal Effects

On the Testable Implications of Causal Models with Hidden Variables

이 둘을 읽고 보면 좋다.

1. Introduction

CEI는 $P_t(y)$가 nonexperimental data로 consistently estimate이 가능한 지에 대한 답이다.

만약, some confounder가 not measured일 때, identifability에 대한 질문이 발생한다.

I 여부는 $T$와 $Y$에 대한 confounder의 위치에 의존한다.

Sufficient criterion으로는 backdoor, frontdoor criterion 등이 있다.

더 일반적으로 위의 criterion들은 do-calculus의 반복에 불과하다.

추가로 펄책의 114-118에서 (backdoor, frontdoor)를 포함하는 sufficient graphical criteria을 보였다.

그 criteria은 longitudinal data에서 unmeasured confounder가 존재해도 time-varying treatment의 effect를 estimate하게 해줬다.

이 논문은 현존하는 criterion을 더 간단하고 더 일반화하는 criteria를 제공한다.

---

Section 3~5에서 unobserved variable이 root 노드이면서 오직 2개의 observed child를 가지는 semi-Markovian model 에서의 I를 다룬다.

Section 3

• CEI of $P_x(v)$ where a sigleton $X \in V$ and $V = V \setminus \{ X\}$
• $X$와 $Ch(X)$가 같은 c-component에 속하지 않음 $<==>$ $P_x(v)$ is identifiable

Section 4

• CEI of $P_x(s)$ where a sigleton $X \in V$ and $S \subseteq V \setminus \{ X\}$
• …

Section 5

• CEI of $P_t(s)$ where a subset $T \subseteq V$ and $S \subseteq V \setminus T$

Section 6

• SMM에 걸린 unobserved node의 조건을 없앤 일반적인 모델을 다룬다.
• 그 모델에서의 CE가 똑같은 I property를 갖는 SMM으로 projection한 뒤에 identify될 수 있음을 보인다.

2.Notation, Definitions, and Problem Formulation

(Skip)

3. Identification of $P_{x}(v)$

(Skip)

General Identification Condition for Causal Effects의 내용과 거의 겹친다.

Identifiability의 필요충분조건에 대한 증명이 더 엄밀해졌다.

4. Identification of $P_x(s)$

• $X \in V$ and $S \subseteq V \setminus \{ X\}$

당연히 $P_x(v)$가 I면 $P_x(s)$도 I다.

하지만, $P_x(v)$가 identifiable하지 않더라도 $P_x(s)$가 identifiable일 수 있다.

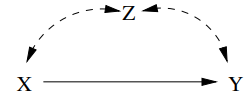
$P_x(y) = P(y \mid x)$로 identifiable하지만, $P_x(y, z)$는 identifiable하지 않다.

$G$에서 의미없는 node들을 쳐낸 뒤에 $P_x(v)$의 identification criterion으로 identify 할 수 있다.

4.1 A criterion for identifying $P_x(s)$

Let $An(C) = C \cup An(C)$

$S$의 ancestrer가 아닌 node들은 $P_x(s)$ identification에 필요하지 않다.

---

Lemma 2

​ $P_x(s)$ is identifiable in $G$ $<==>$ $P_x(s)$ is identifiable in $G_{An(S)}$

(Proof)

<==

​ $\sum_{V \setminus An(S)}P(v) = P(an(S))$

​ 즉, $P_x(s)$가 $P(an(S))$로 구할 수 있음은 $P(v)$로도 구할 수 있음을 의미한다.

==>

​ Lemma 13에서, $G$에서 identifiable했으면, edge들을 좀 빼더라도 identifiable함을 보였다.

---

Lemma 13

​ Let $S,T \subseteq V$ be two disjoint sets of variables.

​ If $P_t(s)$ is not identifiable in $G$, then $P_t(s)$ is not identifiable in $G^+$ where $G^+ = G + \left\{\begin{array}{l} \text{a directed edge} \\ or\\\text{a bidirected edge} \end{array}\right.$

​ Equivalently,

​ If $P_t(s)$ is identifiable in $G$, then $P_t(s)$ is identifiable in $G^-$ where $G^- = G - \left\{\begin{array}{l} \text{a directed edge} \\ or\\\text{a bidirected edge} \end{array}\right.$

(증명 sketch)

• identifiable하지 않을 때 distribution은 같지만
• interventional distribition이 다른 2개의 SCM을 준비한다.
• 2개의 SCM에 대응하여 edge는 넣는 대신에 이를 반영하지 않는 방식으로 결국 같은 SCM을 만든다.

---

Theorem 4 (By Lemma 2)

​ $P_x(s)$ is identifiable if $^{\not \exists}$bidirected path connecting $X$ to $Ch(X)$ in $G_{An(S)}$

(Proof)

​ $G_{An(S)}$에 BP가 없다면, Theorem 3에 의해 $P_x(an(s))$를 구할 수 있다.

​ 추가로 marginalization을 하면 $P_x(s)$를 구할 수 있다.

---

Theorem 4의 조건은 만족하지 못했지만, $P_x(s)$는 identifiable인 예시를 보자.

그리고 이를 통해서 Theorem4의 criterion을 향상시키는 방법에 대한 힌트를 얻어보자.

4.2 An example

$P(v)$를 c-factor로 factorize하는 것을 활용하는 걸 설명하겠다.

$$Q[C](v)=P_{v \backslash c}(c)=\sum_{u} \prod_{\left\{i \mid V_{i} \in C\right\}} P\left(v_{i} \mid p a_{i}, u^{i}\right) P(u)$$

편의를 위해, $Q\left[C\right]$로 표기하겠다. 몇가지 property를 나열하자면,

• $Q\left[V \right] = P(v)$
• $Q\left[ \emptyset \right] = 1$
• $Q\left[ V \right] = \prod _i Q\left[ S_i \right]$ where $S_i$ are the c-component of $G$

---

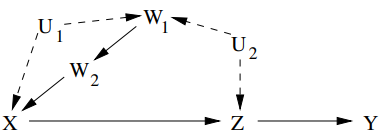
$G_{An(Y)} = G$이고, $X$와 $Z$ 사이에 bidirected path가 있으므로 Theorem 4는 적용 불가능하다.

Let $V = \{ X, Z, Y, W_1, W_2\}$

Let $V’ = \{ Z, Y, W_1, W_2\} = V \setminus \{ X\}$

Then,

• $V$ is partitioned into $\{ W_2\}$, $\{ Y\}$, $S^X = \{ X, Z, W_1\}$
• $P(v) = P(w_2 \mid w_1) P(y \mid z) Q\left[S^X\right]$ where

$$\begin{aligned} Q \left [ S^X\right ] &= \sum_{u_{1}, u_{2}} P\left(x \mid w_{2}, u_{1}\right) P\left(w_{1} \mid u_{1}, u_{2}\right) P\left(z \mid x, u_{2}\right) P\left(u_{1}\right) P\left(u_{2}\right) \\ &= P(w_1) P(x\mid w_2, w_1) P(z \mid x, w_1) \quad \because \text{Lemma 1} \end{aligned}$$

Marginalize as

$$\begin{aligned} P_x(y) &= \sum_{z, w_{1}, w_{2}} P_{x}\left(v^{\prime}\right) \\ &= \sum_{z, w_{1}, w_{2}} Q\left[V' \right] \\ &= \sum_{z, w_{1}, w_{2}} P(w_2 \mid w_1) P(y\mid z) \sum_{u_{1}, u_{2}} P\left(w_{1} \mid u_{1}, u_{2}\right) P\left(z \mid x, u_{2}\right) P\left(u_{1}\right) P\left(u_{2}\right) \\ &= \sum_{z, w_{1}} P(y\mid z) \sum_{u_{1}, u_{2}} P\left(w_{1} \mid u_{1}, u_{2}\right) P\left(z \mid x, u_{2}\right) P\left(u_{1}\right) P\left(u_{2}\right) \quad \text{; $W_2$ out} \\ &= \sum_{z} P(y\mid z) \sum_{u_{1}, u_{2}} P\left(z \mid x, u_{2}\right) P\left(u_{1}\right) P\left(u_{2}\right) \quad \text{; $W_1$ sum-out} \\ &= \sum_{z} P(y\mid z) \sum_{u_{2}} P\left(z \mid x, u_{2}\right) P\left(u_{2}\right) \\ &=\sum_{z} P(y \mid z) Q[\{Z\}] \end{aligned}$$

$W_1$과 $W_2$가 sum-out된 이유는

• $Q[V’]$이 $G_{V’}$의 joint distribution에 대응되고
• $G_{V’}$에서, $W_1$과 $W_2$는 $Y$의 ancestor가 아니였다.

$P_x(y)$는 $Q\left[ \{ Z\}\right]$를 계산하는 문제가 되었고, 이는 $Q[S^X]$로 계산될 수 있다.

$$\begin{aligned} \sum_{w_{1}} Q\left[S^{X}\right] &=Q[\{X, Z\}] \\ &= \sum_{u_{1}, u_{2}} P\left(x \mid w_{2}, u_{1}\right) P\left(z \mid x, u_{2}\right) P\left(u_{1}\right) P\left(u_{2}\right) \\ &= \left(\sum_{u_{1}} P\left(x \mid w_{2}, u_{1}\right) P\left(u_{1}\right)\right)\left(\sum_{u_{2}} P\left(z \mid x, u_{2}\right) P\left(u_{2}\right)\right) \\ &= Q[\{X\}] Q[\{Z\}] \\ \\ \text{Therefore, }\quad \\ Q[\{ X\}] &= \sum_x \sum_{w_{1}} Q\left[S^{X}\right] \\&=\sum_x \sum_{w_{1}} P(w_1) P(x\mid w_2) P(z \mid x, w_1) \\ Q[\{Z\}]&=\frac{\sum_{w_{1}} Q\left[S^{X}\right]}{Q[\{X\}]}=\frac{\sum_{w_{1}} P\left(z, x \mid w_{2}, w_{1}\right) P\left(w_{1}\right)}{\sum_{w_{1}} P\left(x \mid w_{2}, w_{1}\right) P\left(w_{1}\right)} \end{aligned}$$ $$P_{x}(y)=\sum_{z} P(y \mid z) \frac{\sum_{w_{1}} P\left(z, x \mid w_{2}, w_{1}\right) P\left(w_{1}\right)}{\sum_{w_{1}} P\left(x \mid w_{2}, w_{1}\right) P\left(w_{1}\right)}$$

---

$P_x(y)$ identification에 $Q$가 중요한 역할을 한다는 것을 확인했다.

짚고 넘어가야 할 부분

1. $Q \left[ V’\right]$에서 $W_1$과 $W_2$는 $An(Y)_{G(V’)}$에 속하지 않았기에 sum-out 되었다.
2. $Q\left[\{X, Z\}\right] $가 $Q\left[\{X\}\right]$와 $Q\left[\{Z\}\right]$의 product로 표현된 이유는 둘은 $G_{\{ X,Z\}}$에서 c-component이기 떄문이다.

이 아이디어에 착안해서 2개의 Lemma를 도입하겠다.

4.3 Lemmas

특정 조건에서 $Q\left[C\right]$에 summation을 하는 것은 몇몇 factor들을 지우는 행위이다.

이는 $Q\left[C\right]$로부터 $Q\left[W\right]$를 구할 수 있는 지 여부를 제공한다.

여기의 렘마의 증명은 On the Testable Implications of Causal Models with Hidden Variables와 거의 똑같기 때문에 생략함

---

Lemma 3

​ Let $W \subseteq C \subseteq V$ and $W’ = C \setminus W$

​ If $W$ is an ancestral set in $G_C$, then $\sum_{W’} Q\left[ C \right] = Q \left[ W \right]$

---

Lemma 4 (Generalized Q-decomposition)

​ Let $H \subseteq V$

​ Let $H_{1}, \ldots, H_{l}$ be the c-components in the subgraph $G_H$

​ [1] : Then, $Q[H]=\prod_{i} Q\left[H_{i}\right]$

​ Let $k$ be the number of variables in $H$

​ Let a topological order of the variables in $H$ be $V_{h_{1}}<\cdots< V_{h_k}$ in $G_H$

​ Let $H^{(i)}=\left\{V_{h_{1}}, \ldots, V_{h_{i}}\right\}$ and $H^{(0)} = \emptyset$

​ [2] : Then, $Q\left[H_{j}\right] =\prod_{\left\{i \mid V_{h_{i}} \in H_{j}\right\}} \frac{Q\left[H^{(i)}\right]}{Q\left[H^{(i-1)}\right]}$ where $Q\left[H^{(i)}\right] =\sum_{h \backslash h^{(i)}} Q[H] $

$Q\left[H^{(i)}\right] =\sum_{h \backslash h^{(i)}} Q[H] $이 Lemma 3의 inverse임을 인지하여야 함!

​ [3] : Then, $\frac{Q\left[H^{(i)}\right]}{Q\left[H^{(i-1)}\right]}$ is a function only of $P a^{+}\left(T_{i}\right)$ where $T_i$ is a c-component of $G_{H^{(i)}}$ that contains $V_{h_i}$

$T_i$를 점점 커지는 $G(H)$에서 최근에 추가된 노드가 속한 c-component를 생각하면 직감적

---

4.2 example에 Lemma를 적용하면

• $$\begin{aligned} P_x(y) &= \sum_{z, w_{1}, w_{2}} P_{x}\left(v^{\prime}\right) \\ &= \sum_{z, w_{1}, w_{2}} Q\left[V' \right] \\ &= \sum_{z, w_{1}, w_{2}} P(w_2 \mid w_1) P(y\mid z) \sum_{u_{1}, u_{2}} P\left(w_{1} \mid u_{1}, u_{2}\right) P\left(z \mid x, u_{2}\right) P\left(u_{1}\right) P\left(u_{2}\right) \\ &= \sum_{z, w_{1}} P(y\mid z) \sum_{u_{1}, u_{2}} P\left(w_{1} \mid u_{1}, u_{2}\right) P\left(z \mid x, u_{2}\right) P\left(u_{1}\right) P\left(u_{2}\right) \quad \text{; $W_2$ out} \\ &= \sum_{z} P(y\mid z) \sum_{u_{1}, u_{2}} P\left(z \mid x, u_{2}\right) P\left(u_{1}\right) P\left(u_{2}\right) \quad \text{; $W_1$ sum-out} \\ &= \sum_{z} P(y\mid z) \sum_{u_{2}} P\left(z \mid x, u_{2}\right) P\left(u_{2}\right) \\ &=\sum_{z} P(y \mid z) Q[\{Z\}] \end{aligned}$$

• $S^X = \{ X, W_1, Z\}$에서 $H=\{X, Z \}$로 둘 경우, $\{ X\}, \{Z\}$로 분리된다.

• 그 경우, $H^{(1)} = \{ X\}$ , $H^{(2)} = \{ X, Z\}$

• $$\begin{aligned} Q\left[Z\right] &= \frac{Q \left[ H^{(2)}\right]} { Q\left[ H^{(1)} \right ]} \\ &= \frac{Q \left[\{ X, Z\}\right]} { Q\left[ \{ X\} \right ]} \quad \because \text{Lemma 4 [2]}\\ &= \frac{Q \left[\{ X, Z\}\right]}{\sum_{z} Q \left[\{ X, Z\}\right]} \quad \because \text{Lemma 4 [2]} \\ &= \frac{ \sum _{w_1} Q \left[S^X\right]}{\sum_{w_1, z} Q \left[S^X\right]} \quad \because \text{Lemma 3}\\ &= \frac{\sum_{w_{1}} P\left(z, x \mid w_{2}, w_{1}\right) P\left(w_{1}\right)}{\sum_{w_{1}} P\left(x \mid w_{2}, w_{1}\right) P\left(w_{1}\right)} \end{aligned}$$

• Lemma 4 [3]에 의하면, $Q\left [Z\right ]$는 $w_2$에 의존하지 않는다.

• Functional constraints를 체계적으로 찾는 방법은 On the Testable Implications of Causal Models with Hidden Variables에 나와있다.

---

Lemma 1, 3, 4에 기반하여 $P_x(s)$를 체계적으로 계산해보자.

4.4 Computing $P_x(s)$

Let $V$ be partitioned into c-components $S^X, S_1, \ldots, S_k$ where $X \in S^X$.

Let $V’ = V \setminus \{X\}$. Then,

• $P(v) = Q\left[V \right] = Q[\left[ S^X \right ]] \prod _i Q \left[ S_i \right]$
• $P_x(v’) = Q\left [V’ \right ] = Q\left[ S^X \setminus \{ X\}\right] \prod _i Q \left[ S_i \right]$

We want to compute $P_x(s) = \sum_{v’ \setminus s} P_x(v’) = \sum_{v’ \setminus s} Q\left [V’ \right ]$

• Let $D = An(S)_{G_{V’}}$
• Since $D$ is ancestral set in $G_{V’}$,
  • $\sum_{v^{\prime} \setminus d} Q\left[V^{\prime}\right] = Q\left[D \right]$
• Therefore,
  • $P_x(s) = \sum_{v’ \setminus s} Q\left [V’ \right ] = \sum_{d \setminus s} \sum_{v^{\prime} \setminus d} Q\left[V^{\prime}\right] = \sum_{d \setminus s} Q\left[D \right]$

---

Let $D^X = D \cap S^X$ and $D_i = D\cap S_i$. Then,

• $\begin{aligned}Q\left[D \right] &=\sum_{v^{\prime} \setminus d} Q\left[V^{\prime}\right] \\& = \sum_{v^{\prime} \setminus d} Q\left[ S^X \setminus \{ X\}\right] \prod _i Q \left[ S_i \right] \\& = Q\left[D^{X}\right] \prod_{i} Q\left[D_{i}\right] \end{aligned}$
  • $D_i$가 $G_{S_i}$에서 ancestral set이기에 $\sum_{v^{\prime} \setminus d}$를 가장 말단 노드부터 하다보면 위 처럼 factorize될 것임이 자명하다.
• $Q\left[D_{i}\right]=\sum_{s_{i} \setminus d_{i}} Q\left[S_{i}\right], \quad i=1, \ldots, k$
  • $D_i$가 $G_{S_i}$에서 ancestral set이기에 Lemma 3 적용

---

지금까지의 derivation을 풀어쓰면

$$\begin{aligned} P_x(s) &= \sum_{v' \setminus s} P_x(v') = \sum_{d \setminus s} \sum_{v^{\prime} \setminus d} Q\left[V^{\prime}\right] \\ &= \sum_{d \setminus s}Q\left[D \right] \\ &= \sum_{d \setminus s} Q\left[D^{X}\right] \prod_{i} Q\left[D_{i}\right] \\ &= \sum_{d \setminus s} Q\left[D^{X}\right] \prod_{i} \sum_{s_{i} \setminus d_{i}} Q\left[S_{i}\right] \end{aligned}$$

추가로 $G_{D^{X}}$에서 $D_{1}^{X}, \ldots, D_{l}^{X}$로 c-component partition이 나눠진다면,

$$P_{x}(s)=\sum_{d \setminus s} \prod_{j} Q\left[D_{j}^{X}\right] \prod_{i} \sum_{s_{i} \setminus d_{i}} Q\left[S_{i}\right]$$

$D_j^X \subset S^X$ 이기 때문에, $Q \left [ D_j^X\right]$가 $Q\left [ S^X\right]$로 계산될 수 있으면 이는 identifiable하다.

이제 $Q \left [ D_j^X\right]$를 $Q\left [ S^X\right]$로 계산해보도록 하자.

---

Let $F = An(D_j^X)_{G_{S^X}}$

$Q\left [F\right]$는 identifiable함

• 만약 $F = D_j^X$인 경우,
  • Lemma 3에 의해, $Q\left[D_{j}^{X}\right]=\sum_{S^{X} \backslash D_{j}^{X}} Q\left[S^{X}\right]$
• 만약 $F=S^X$인 경우,
  • 실패
  • (이 실패가 non-identifiability를 의미하는 지는 의문)
• 만약 $D_j^X \subset F \subset S^X$인 경우,
  • Lemma 3에 의해, $Q\left[F\right]=\sum_{S^{X} \backslash F} Q\left[S^{X}\right]$
  • $F \subset S^X$ 이기 때문에, $Q \left [ D_j^X\right]$가 $Q\left [ F\right]$로 계산될 수 있으면 $Q\left[S^{X}\right]$로도 구해질 수 있다.
  • $H :=$ c-component containing $D_j^X$ in $G_F$
  • Lemma 4에 의해, $Q\left[H\right]$는 $Q\left[F\right]$로 구해질 수 있다.
  • $Q \left [ D_j^X\right]$를 구하는 문제를 $Q\left [ S^X\right] \Rightarrow Q\left[F\right] \Rightarrow Q\left[H\right]$로 구하는 문제로 줄였다.

---

위의 결과는 $Q\left [ D_j^X\right]$가 $Q\left[ S^X\right]$로 구해질 수 있는 지를 결정하는 과정을 제공한다.

1. $Q\left [ D_j^X\right]$를 구하거나
2. 실패하거나
3. 더 간단한 $H \subset S^X$로 문제를 줄이거나

$C \subset T \subset V$에 대해서, $Q\left[ C \right]$가 $Q\left[T\right]$로 구해질 수 있는 가에 대한 일반적인 함수

$P_x(s)$를 구하는 알고리즘

4.5 Useful graphical criteria

위에서 identifiability를 결정하고 그 경우에 이를 계산하는 알고리즘을 제공하였다.

빠르게 identifiability 결정에 사용할 수 있는 graphical criteria를 설명하겠다.

주된 아이디어는 중요하지 않은 노드들을 체계적으로 제거하는 것이다.

1. $V \setminus An(S)$ 제거 (Lemma 2)
2. $V \setminus S^X$ 제거 (Lemma 6)

---

Let $A \subseteq B \subseteq V$

Let $Q\left[A \right]_{G_B}=\sum_{u} \prod_{\left\{i \mid V_{i} \in A\right\}} P\left(v_{i} \mid p a_{i}^{\prime}, u^{i}\right) P(u)$ where $P A_{i}^{\prime}=P A_{i} \cap B$

Let $Q\left[A\right] = Q\left[ A\right]_{G_V}$

---

Lemma 5

​ Let $A \subseteq B \subseteq V$

• $Q\left[A\right]$ is computable from $Q\left[B\right]$
• iff
• $Q\left[A\right]_{G_B}$ is computable from $Q\left[B\right]_{G_B}$

==> 증명은 Lemma 13의 적용, <== 증명은 귀류법

---

Lemma 6 (reduce identification problem)

​ Let $D^X = A n(S)_{G_{V \backslash\{X\}}} \cap S^X$

​ Then, $P_x(s)$ is identifiable if $P_x(D^X)$ is identifiable in $G_{S^X}$

(Proof)

​ 4.4에서 $P_x(s) = \sum_{d \setminus s} Q\left[D^{X}\right] \prod_{i} \sum_{s_{i} \setminus d_{i}} Q\left[S_{i}\right]$ 임을 보였다.

​ 그래서 $Q\left[D^X\right]$가 identifiable이면 $P_x(s)$도 identifiable임을 보였다.

​ Lemma 5에 의해, $Q\left[D^X\right]_{S^X}$가 identifiable이면, $Q\left[D^X\right]$도 identifiable이다.

​ Let $E^X = S^X \setminus \{D^X \cup X \}$. Then,

$$\begin{aligned} P_{x}\left(D^{X}\right)_{S^X} &= \sum_{E^{X}} P_{x}\left(S^{X} \backslash\{X\}\right) \\ &= \sum_{E^{X}} Q\left[S^{X} \backslash\{X\}\right]_{G_{S ^X}} \\ &= Q\left[D^{X}\right]_{G_{S^X}} \end{aligned}$$

​ 즉, $P_x(D^X)$가 $G_{S^X}$에서 identifiable이면, $P_x(s)$는 identifiable이다.

4.6 An Example

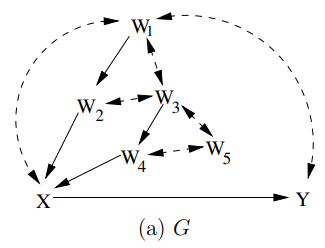
$P_x(y)$를 고려해보자.

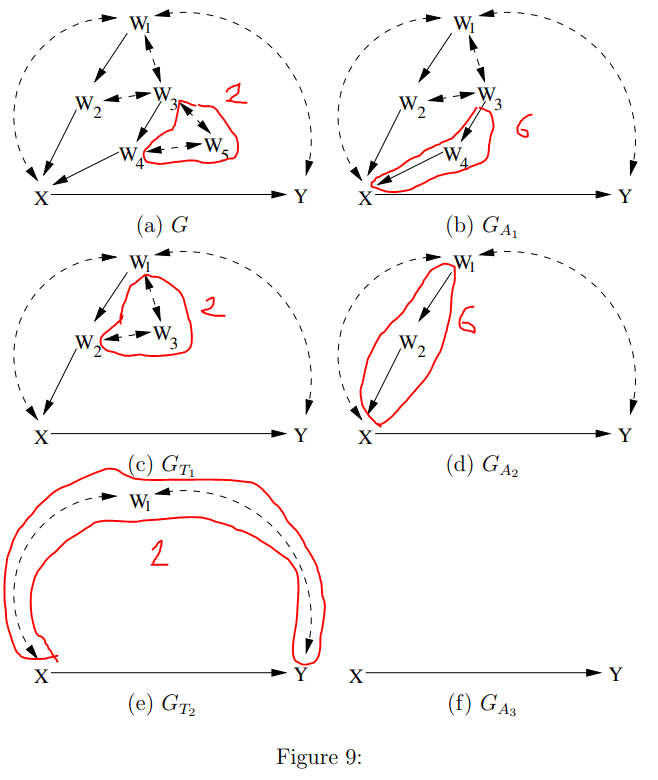
Lemma 2와 Lemma 6의 반복으로 identifiable하다는 것까지는 확인할 수 있다.

이제 이를 구해보도록 하자.

Phase 1

1. $G$ has one c-component $S^X$
2. Compute ; $Q\left [ S^X \right] = P(v)$
3. Let $D = A n( \{ Y\})_{G_{V \backslash\{X\}}} = \{ Y\}$ and $D^X = D \cap S^X = \{ Y\}$
4. Let the c-compont of $G_{D^X}$ be $D_1^X = \{ Y \}$

Phase 2

1. Identify$ \left (\{Y \}, V, P(v) \right)$

   1. Let $A_1 = An(\{ Y\}) = \{ X, Y, W_{1:4}\}$

   2. $G_{A_1}$ has two c-components $T_{1}=\left\{X, Y, W_{1}, W_{2}, W_{3}\right\}$ and $\left\{W_{4}\right\}$

      $$\begin{aligned} Q\left[A_{1}\right]&=\sum_{w_{5}} P(v) \quad \because \text{Lemma 3} \\ &=P\left(a_{1}\right) \\ &=Q\left[T_{1}\right] Q\left[\left\{W_{4}\right\}\right] \end{aligned}$$

   3. topological order in $G_{A_1}$ : $W_{3}<W_{4}<W_{1}<W_{2}<X<Y$

      $$\begin{aligned} Q\left[\left\{W_{4}\right\}\right]&=\frac{Q\left[\left\{W_{4}, W_{3}\right\}\right]}{Q\left[\left\{W_{3}\right\}\right]} \quad \because \text{Lemma 4} \\ &=\frac{\sum_{w_{1}, w_{2}, x, y} P\left(a_{1}\right)}{\sum_{w_{4}, w_{1}, w_{2}, x, y} P\left(a_{1}\right)} \\ &= \frac{P(w_3, w_4)}{P(w_3)} \\ &=P\left(w_{4} \mid w_{3}\right) \end{aligned}$$
   4. $$\begin{aligned} Q\left[T_{1}\right]&= \frac{Q[A_1]}{Q [\{ W_4\}]} \\ &= \frac{P(a_1)}{P(w_4 \mid w_3)} \\ &= P(x,y ,w_1, w_2 \mid w_3, w_4) P(w_3) \\ &= P(x, y \mid w_1, w_2, w_3, w_4) P(w_1, w_2 \mid w_3, w_4)P(w_3) \\ &= P(x, y \mid w_1, w_2, w_3, w_4) P(w_1, w_2, w_3) \quad \because \{ W_1, W_2\} \perp W_4 \mid W_3 \end{aligned}$$

2. Identify(Identify$ \left (\{Y \}, T_1, Q\left[T_1 \right] \right)$

   1. Let $A_2 = An(\{ Y\})_{G_{T_1}} = \{ X, Y, W_1, W_2 \}$

   2. $G_{A_2}$ has two c-components $T_{2}=\left\{X, Y, W_{1}\right\}$ and $\left\{W_{2}\right\}$

      $$\begin{aligned} Q\left[A_{2}\right]&=\sum_{w_3} Q[T_1] \quad \because \text{Lemma 3} \\ &=Q\left[T_{2}\right] Q\left[\left\{W_{2}\right\}\right] \end{aligned}$$

   3. topological order in $G_{A_2}$ : $W_{1}<W_{2}<X<Y$

      $$\begin{aligned} Q\left[\left\{W_{2}\right\}\right]&=\frac{Q\left[\left\{W_{2}, W_{1}\right\}\right]}{Q\left[\left\{W_{1}\right\}\right]} \quad \because \text{Lemma 4} \\ &=\frac{\sum_{x, y} Q\left[A_{2}\right]}{\sum_{w_{2}, x, y} Q\left[A_{2}\right]} \\ &=\frac{\sum_{w_3, x, y} Q[T_1]}{\sum_{w_{2},w_3 x, y} Q[T_1]} \\ &= \frac{\sum_{w_3, x, y} P(x, y \mid w_1, w_2, w_3, w_4) P(w_1, w_2, w_3) }{\sum_{w_2, w_3, x, y} P(x, y \mid w_1, w_2, w_3, w_4) P(w_1, w_2, w_3) } \\ &=\frac{\sum_{w_3, x, y} P(x, y \mid w_1, w_2, w_3, w_4) P(w_1) P(w_2\mid w_1) P( w_3 \mid w_1, w_2) }{\sum_{w_2, w_3, x, y} P(x, y \mid w_1, w_2, w_3, w_4) P(w_1) P(w_2\mid w_1) P( w_3 \mid w_1, w_2)} \\ &= \frac{P(w_2\mid w_1) \times\sum_{w_3, x, y} P(x, y \mid w_1, w_2, w_3, w_4) P( w_3 \mid w_1, w_2) }{\sum_{w_2, w_3, x, y} P(x, y \mid w_1, w_2, w_3, w_4) P(w_2\mid w_1) P( w_3 \mid w_1, w_2)} \\ &= P(w_2\mid w_1) \end{aligned}$$
   4. $$\begin{aligned} Q\left[T_{2}\right]&= \frac{Q[A_2]}{Q [\{ W_2\}]} \\ &= \frac{\sum_{w_3} Q[T_1] }{P(w_2 \mid w_1)} \\ &=\frac{\sum_{w_3}P(x, y \mid w_1, w_2, w_3, w_4) P(w_1, w_2, w_3) }{P(w_2 \mid w_1)} \\ &=\sum_{w_{3}} P\left(x, y \mid w_{1}, w_{2}, w_{3}, w_{4}\right) P\left(w_{3} \mid w_{1}, w_{2}\right) P\left(w_{1}\right) \end{aligned}$$

3. Identify(Identify$ \left (\{Y \}, T_2, Q\left[T_2 \right] \right)$

   1. Let $A_3 = An(\{ Y\})_{G_{T_2}} = \{X, Y \}$

   2. $G_{A_3}$ has two c-components $\{ X\}$ and $\{ Y\}$

      $$\begin{aligned} Q\left[A_{3}\right]&=\sum_{y} Q[T_2] \quad \because \text{Lemma 3} \\ &=Q\left[ \{X \}\right] Q\left[\left\{Y\right\}\right] \end{aligned}$$

   3. topological order in $G_{A_3}$ : $X < Y$

      $$\begin{aligned} Q\left[\left\{X\right\}\right]&= \sum_{y} Q[A_3] \\ &= \sum_y \sum_{w_1}Q[T_2] \\ &= \sum_y \sum_{w_1}Q[T_2] \\ &= \sum_y \sum_{w_1}\sum_{w_{3}} P\left(x, y \mid w_{1}, w_{2}, w_{3}, w_{4}\right) P\left(w_{3} \mid w_{1}, w_{2}\right) P\left(w_{1}\right) \\ &= \sum_{w_1}\sum_{w_{3}} P\left(x \mid w_{1}, w_{2}, w_{3}, w_{4}\right) P\left(w_{3} \mid w_{1}, w_{2}\right) P\left(w_{1}\right) \end{aligned}$$
   4. $$\begin{aligned} Q\left[ \{ Y\}\right]&= \frac{\sum_{y} Q[T_2]}{Q [\{ X\}]} \\ &= \frac{\sum_{y} \sum_{w_{3}} P\left(x, y \mid w_{1}, w_{2}, w_{3}, w_{4}\right) P\left(w_{3} \mid w_{1}, w_{2}\right) P\left(w_{1}\right) }{\sum_{w_1}\sum_{w_{3}} P\left(x \mid w_{1}, w_{2}, w_{3}, w_{4}\right) P\left(w_{3} \mid w_{1}, w_{2}\right) P\left(w_{1}\right)} \\ &=\frac{\sum_{w_3}P(x, y \mid w_1, w_2, w_3, w_4) P(w_1, w_2, w_3) }{P(w_2 \mid w_1)} \end{aligned}$$

Phase 3

$$P_{x}(y)=Q[\{Y\}]=\frac{\sum_{w_{1}, w_{3}} P\left(x, y \mid w_{1}, w_{2}, w_{3}, w_{4}\right) P\left(w_{3} \mid w_{1}, w_{2}\right) P\left(w_{1}\right)}{\sum_{w_{1}, w_{3}} P\left(x \mid w_{1}, w_{2}, w_{3}, w_{4}\right) P\left(w_{3} \mid w_{1}, w_{2}\right) P\left(w_{1}\right)}$$

4.7 Galles&Pearl’s graphical criterion vs. do-calculus

Galles and Pearl, 1995은 그들의 G-criteria가 do-calculus로 증명될 수 있는 identifiability를 모두 포함한다고 주장했으나, 그렇지 않았다.

skip

5. Identification of $P_t(s)$

이제까지 intervention은 single variable $X$에만 적용됐다.

이번 섹션에서, 임의의 $T \subset V$에 대해서 intervention을 하겠다.

$P_t(s)$ identification도 identifying $Q\left[C\right]$ from $Q\left[C’\right]$ 으로 줄어듦을 보이겠다.

5.1 Computing $P_t(s)$

Let $T’=V \setminus T$

We want to compute $P_{t}(s)=\sum_{T^{\prime} \setminus S} P_{t}\left(t^{\prime}\right)=\sum_{T^{\prime} \setminus S} Q\left[T^{\prime}\right]$

Let $D = An(S)_{G_{T’}}$

Then,

$$\begin{aligned} P_{t}(s)&=\sum_{D \setminus S} \sum_{T^{\prime} \setminus D} Q\left[T^{\prime}\right] \\ &=\sum_{D \setminus S} Q[D] \quad \because \text{Lemma 3} \\ &=\sum_{D \setminus S} \prod_{i} Q\left[D_{i}\right] \quad\text{where $D$ is partitioned into $D_1, \cdots, D_l$} \end{aligned}$$

Hence if all $Q\left[D_i\right]$ are identifiable, $P_t(s)$ is identifiable.

Let $V$ be partitioned into c-components $S_1, \cdots, S_k$

Then, any $D_i$ is a subset of certain $S_j$

$D_i$안의 변수들은 서로 $G$상의 BP로 연결됐다. 결국 $D_i$는 특정 c-component에 속한다.

$D_i \subseteq S_j$라면, $Q\left[D_i\right]$의 identifiability는 identify($D_i, S_j, Q\left[ S_j\right]$)로 결정될 수 있다.

5.2 Useful graphical criteria

다음으로, 그래프만으로 빠르게 identifiability를 결정한 graphical criteria를 보이겠다.

Let $T’ = V \setminus T$

우선 $P_t(t’)$에서 보이겠다.

---

Theorem 5

​ If ${}^{\not\exists}$BE btw $T \sim T’$, then $P_t(t’)$ is identifiable.

​ Let a topological order over $V$ be $V_{1}<\ldots<V_{n}$

​ Let $V^{(i)} = \{V_1, \cdots, V_i \}$ for $i=1, \cdots, n$ and $V^{(0)} = \emptyset$

​ Then by Lemma 1,

$$P_{t}(t')=\prod_{\left\{i \mid V_{i} \in T'\right\}} P\left(v_{i} \mid p a\left(C_{i}\right) \setminus \left\{v_{i}\right\}\right) \quad \text{where $C_i$ is the c-component of $G_{V^{(i)}}$ that contains $V_i$}$$

---

Let $V$ be partitioned into $S_1, \cdots, S_k$

Let $T_i = T \cap S_i$ and $T_i’ = T’ \cap S_i$ for $i=1, \cdots, k$

• Since $P_{t}\left(t^{\prime}\right) =Q\left[T ^\prime \right] =\prod_{i} Q\left[T_{i}^{\prime}\right]$

  • $P_t(t’)$ is identifiable iff each $Q\left[ T_i’ \right]$ is computable from $Q\left [ S_i\right]$

• Since $P_{t_{j}}\left(v \backslash t_{j}\right)=Q\left[T_{j}^{\prime}\right] \prod_{i \neq j} Q\left[S_{i}\right]$

  • $P_{t_j}(v \setminus t_j)$ is identifiable iff each $Q\left[ T_j’\right]$ is computable from $Q\left [ S_j\right]$

---

Lemma 7

​ Let $V$ be partitioned into c-components $S_1, \cdots , S_k$

​ Let $T_i = T \cap S_i$ for $i=1 , \cdots , k$

​ Then, $P_{t}(t’)$ is identifiable iff $P_{t_i} (v \setminus t_i)$ is identifiable for every $i=1, \cdots, k$

---

In the subgraph $G_{S_i}$,

1. $P(s_i) = Q\left[S_i\right]_{G_{S_i}}$
2. $P_{t_i} (s_i \setminus t_i) = Q \left[ T_i’\right]_{G_{S_i}}$

Lemma 8

• By Lemma 5,
  • $ Q\left[ T_i ‘ \right]$ is computable from $Q\left[ S_i\right]$ iff $P_{t_i}(s_i \setminus t_i)$ is identifiable in $G_{S_i}$

---

$Q \left[ T_i ‘ \right]$ is computable from $Q\left[ S_i\right]$ 의 가장 간단한 조건은 $T_i’$이 ancestral set일 때다.

Theorem 6

​ Let $S_i$ be a c-component of $G$

​ Let $T_i \subseteq S_i$

​ If the children of variables in $T_i$ are either

• in $T_i$ or

• outside of $S_i$

  then identifiable and can be computed from $Q\left[ S_i\right]$

$$P_{t_{i}}\left(v \setminus t_{i}\right)=\frac{P(v)}{Q\left[S_{i}\right]} \sum_{T_{i}} Q\left[S_{i}\right]$$

---

이제 graphical criteria for identifiability of $P_t(s)$ 를 알아보자.

Lemma 9

​ Let $D = An(S)_{G_{V\setminus T}}$

​ Let $V$ be partitioned into c-components $S_1, \cdots, S_k$.

​ Let $T_i = T \cap S_i$ and $D_i = D \cap S_i$ for $i=1, \cdots, k$

​ Then, $P_t(s)$ is identifiable if $P_{t_i}(d_i)$ is identifiable in $G_{S_i}$ for every $i=1, \cdots, k$

(Proof)

​ Since $P_{t}(s) = \sum_{D \setminus S} \prod_{i} Q\left[D_{i}\right]$, $P_t(s)$ is identifiable if each $Q\left[ D_i\right]$ is identifiable.

​ By Lemma 5, $Q\left[ D_i\right]$ is computable from $Q\left[ S_i\right]$ iff $Q\left[D_i\right]_{G_{S_i}}$ is computable from $Q[S_i]_{G_{S_i}}$

​ Let $T_i’ = S_i \setminus T_i$

​ Since $P_{t_{i}}\left(d_{i}\right)=\sum_{T_{i}^{\prime} \backslash D_{i}} P_{t_{i}}\left(t_{i}^{\prime}\right)=\sum_{T_{i}^{\prime} \backslash D_{i}} Q\left[T_{i}^{\prime}\right]_{G_{S_{i}}}=Q\left[D_{i}\right]_{G_{S_{i}}}$, it’s all done.

---

Lemma 10

​ Let $T_1 = T \cap An(S)$

​ $P_t(s)$ is identifiable iff $P_{t_1}(s)$ is identifiable in $G_{An(S)}$

---

Lemma 9와 10은 $P_t(s)$ identification을 subgraph에서의 문제로 줄여준다.

줄여진 문제는 Theorem 4와 6으로 적용가능해진다.

5.3 Examples

Let $T= \{ X_1, X_2\}$ and $S = \{Y\}$

Phase-1

1. c-components $S_1 := \{ X_1, Z, Y\}, S_2:= \{ X_2\}$

2. $Q\left[ S_1\right] = P\left(y \mid x_{1}, x_{2}, z\right) P(x_{1}) P( z \mid x_1)$

   $Q\left[ S_2\right] = P\left(x_2 \mid x_{1}, z\right)$

3. $D:= An(\{ Y \})_{G_{V \setminus \{ X_1, X_2\}}} = \{ Y\}$

4. $D_1 := D \cap S_1 =\{ Y\}$, $D_2 := D \cap S_2 = \emptyset$

graphical criteria

• Lemma 9 : $P_{x_1, x_2}(y)$ is identifiable if $P_{x_1}(y)$ is identifiable in $G_{S_1}$

• Theorem 4 : $P_{x_1}(y)$ is identifiable in $G_{S_1}$

Phase-2

• $Identify(D_1, S_1, Q \left[ S_1\right])$
  • Let $A = An(D_1)_{G_{S_1}} = \{ X_1, Y\}$
  • Since $D_1 \subset A \subset S$,
    • $G_A$ has two c-components $T^\prime :=\{Y \}$, $\{ X_1\}$
    • $\begin{aligned} Q\left[ A\right] &= \sum_{S_1 \setminus A}Q\left[ S_1\right] \\&= Q \left[ \{X_1, Y \}\right] \quad \because \text{Lemma 3}\\&= Q\left[\left\{X_{1}\right\}\right] Q[\{Y\}] \quad \because \text{Lemma 4}\end{aligned}$
    • $\begin{aligned} Q\left[ X_1\right] &= P(x_1)\end{aligned}$
    • $\begin{aligned} Q\left[ Y_1 \right] &= Q\left[ A\right] / Q\left[\{ X_1\} \right] \\&= \sum_{z} Q[S] / Q\left[\left\{X_{1}\right\}\right] \\ &= \sum_{z} P\left(y \mid x_{1}, x_{2}, z\right) P\left(z \mid x_{1}\right)\end{aligned}$

Phase-3

• $\begin{aligned}P_{t}(s)&=\sum_{D \backslash S} \prod_{i} Q\left[D_{i}\right] \\ &= Q\left[ D_1\right] \\ &= Q\left[ \{ Y\}\right] \\ &= \sum_{z} P\left(y \mid x_{1}, x_{2}, z\right) P\left(z \mid x_{1}\right)\end{aligned}$

---

Let $T = \{ X_1, X_2\}$ and $S = \{ Y\}$

Phase-1

1. c-components $S_1 := \{ X_2, W, Y\}, S_2:= \{ X_1\}$

2. $Q\left[ S_1\right] = P\left(y \mid x_{2}, w\right) P(x_{2} \mid x_1) P( w \mid x_2)$

   $Q\left[ S_2\right] = P\left(x_1 \right)$

3. $D:= An(\{ Y \})_{G_{V \setminus \{ X_1, X_2\}}} = \{ Y\}$

4. $D_1 := D \cap S_1 =\{ Y\}$, $D_2 := D \cap S_2 = \emptyset$

graphical criteria

• Lemma 9 : $P_{x_1, x_2}(y)$ is identifiable if $P_{x_2}(y)$ is identifiable in $G_{S_1}$
• Theorem 4 : $P_{x_2}(y)$ is identifiable in $G_{S_1}$

…

---

Let $T = \{ X_1, X_2\}$ and $S = \{ Y\}$

Phase-1

1. c-components $S_1 := \{ X_1 \} , S_2:= \{Y \}, S_3 := \{ X_2, Z_1, Z_1^\prime \}$
2. …

graphical criteria

• Lemma 7 : $P_{x_{1} x_{2}}(y)$ is identifiable if $P_{x_{1}}(v)$ and $P_{x_{2}}(v)$ are identifiable
• Theorem 3 : $P_{x_{1}}(v)$ and $P_{x_{2}}(v)$ are identifiable

Compute $P_t(t^\prime)$

$$\begin{aligned} P_t(t^\prime) & =Q\left[T^\prime\right] \\&=\prod_i Q\left[ T_i^\prime\right] \\&=Q\left[ \{ Y\}\right] Q\left[ \{ Z_1, Z_1^\prime\}\right] \\&=P\left(y \mid x_{2}, z_{1}^{\prime}\right) \sum_{x_{2}} Q\left[S\right] \\&=P\left(y \mid x_{2}, z_{1}^{\prime}\right) P\left(z_{1}^{\prime}, z_{1}\right) \end{aligned}$$

---

Let $T = \{ X_1, X_2\}$ and $S = \{ Y\}$

Phase-1

1. c-components $S_1 := \{ X_1, X_2, Y \} , S_2:= \{Z_1 \}, S_3 := \{ Z_2 \}$
2. $T_1 := S_1 \cap T = \{ X_1, X_2 \}$

graphical criteria + compute $P_{t_i}( v \setminus t_i)$

• Theorem 6 : $P_{T_1}(v \setminus t_i)$ is identifiable
• $P_{t_{1}}\left(v \setminus t_{1}\right)=\frac{P(v)}{Q\left[S_{1}\right]} \sum_{T_{1}} Q\left[S_{1}\right] =P\left(z_{1} \mid x_{1}\right) P\left(z_{2} \mid x_{1}, x_{2}\right) \sum_{x_{1}^{\prime}, x_{2}^{\prime}} P\left(y \mid x_{1}^{\prime}, x_{2}^{\prime}, z_{1}, z_{2}\right) P\left(x_{2}^{\prime} \mid x_{1}^{\prime}, z_{1}\right) P\left(x_{1}^{\prime}\right) .$
• $P_{x_{1} x_{2}}(y)=\sum_{z_{1}, z_{2}} P\left(z_{1} \mid x_{1}\right) P\left(z_{2} \mid x_{1}, x_{2}\right) \sum_{x_{1}^{\prime}, x_{2}^{\prime}} P\left(y \mid x_{1}^{\prime}, x_{2}^{\prime}, z_{1}, z_{2}\right) P\left(x_{2}^{\prime} \mid x_{1}^{\prime}, z_{1}\right) P\left(x_{1}^{\prime}\right)$