Stochastic Sequential Neural Networks with Structured Inference

0. Abstract

High dimensional time series(HDTS)에서 unsupervised learning은 많은 연구에서 관심을 끌고 있다.

특히 HDTS에서 segmentation을 하는 것은 행동 패턴에 대한 이해에 도움이 될 수 있다.

최근 generative sequential modeling에서 RNN과 State Space Model(SSM)의 결합이 제안되고 있다.

SSM은 HMM과 Kalman filter 등을 포함하는 PGM의 class이다.

이를 Stochastic Sequential Neural Network(SSNN) 으로 부르겠다.

SSNN은 long term dependency와 uncertainty in hidden state도 모델링할 수 있다.

여기서의 uncertainty는 VRNN에서의 variability와 같은 표현 같다.

SSNN에

• discrete latent variable을 활용한 structured inference를 더하여 segmentation을 수행한다.
• 정확하고 효율적인 inference를 위해, bi-directional inference network를 제안한다.

제시하는 모델은

1. speech modeling
2. automatic segmentation in behavior understanding
3. sequential multi-objects recognition

에서 검증된다.

1. Introduction

HDTS에서 unsupervised structure learning은 기계번역, 음성인식, 계산생물학 등에서 중요하다.

예를 들어, medical diagnosis에서 복잡한 물리적 신호의 segmentation은 의사들에게 잠재된 행동을 이해하는 데에 도움을 줄 수 있다.

Sequential data를 이한 모델링에 RNN과 HMM이 주로 사용된다.

최근 probabilistic generative model에 RNN을 결합하는 연구들이 있다.

Johnson, 2016, Dai, 2017b, Fraccaro, 2016

Segmentation of natural scene & physiological signal task에서 segmentation은 해석 가능한 이산형 분포이다.

Neural network로 discrete latent variable를 inference하는 데에 어려움이 있기 때문에, 대부분의 모델은 continuous latent variable만 고려한다.

비록 Dai, 2017b는 discrete variable을 segmentation 예측에 활용하였으나 bi-directional temporal information을 명시적으로 활용하지 않았기에 낮은 performance를 갖는다.

이러한 문제들을 해결하기 위해 generative network와 inference network로 구성된 SSNN을 제안한다.

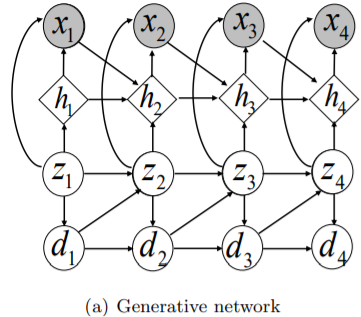
Generative network는

• Hidden Semi-Markov Model(HSMM)과 Recurrent HSMM Dai, 2017b에 기반한다.
• Continuous RNN hidden state와 SSM의 discrete latent variable로 구성된다.

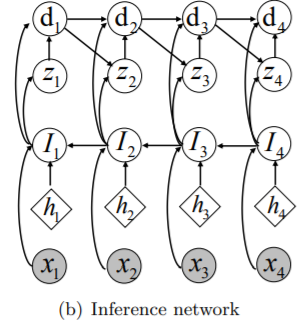
Inference network는

• bi-directional temporal information을 활용하여 정확하고 효율적으로 inference를 한다.

의도를 이해하려면, Dai, 2017b, Krishnan et al., 2016 는 읽어봐야 할 듯 하다.

제안하는 SSNN은

• 기존의 sequential data의 complex and long range dependency 모델링은 유지하고
• 추가로 효율적인 inference를 통해 SSM의 structure learning 능력을 추가한다.

제안하는 모델의 performance를 평가하기 위해

1. speech modeling 데이터 셋의 segmentation
2. Behavior modeling 데이터 셋의 segmentation
3. multi-object recognition 데이터 셋의 segmentation

에서 비교실험을 한다.

2. Preliminaries

RNN 관련한 내용은 스킵

---

HMM과 HSMM은 sequential learning에서 널리 쓰인다.

HMM은 각 $\mathbf{x}_{t}$가 hidden state $z_{t} \in\{1,2, \ldots, K\}$에 의해 생성됐다고 가정한다.

• Emission probability $p_{\theta}\left(\mathbf{x}_{t} \mid z_{t}\right)$
• Initial hidden state distribution $p_{\theta}\left(z_{1}\right)$
• Transition probability $p_{\theta}\left(z_{t} \mid z_{t-1}\right)$

---

HSMM은 HMM의 유명한 extension이다.

이는 추가로 time duration variable $d_{t} \in\{1,2, . ., M\}$을 도입하였다.

이 때, $M$은 segment가 가질 수 있는 최장 길이를 의미한다.

HSMM은 $\mathbf{x}_{1: T}$를 $L$개의 segment로 분해한다.

$L$개의 segment의 시작점들을 $\mathbf{s}_{1: L}=\left[s_{1}, s_{2}, . ., s_{L}\right]$로 두겠다.

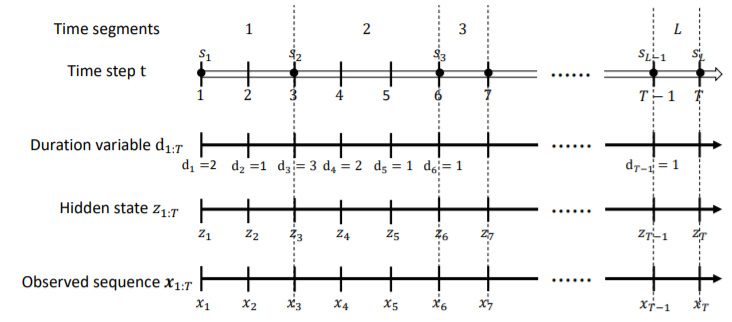
$i$번 째 segment의 시작점 $s_i$ 부터 $s_{i}+d_{s_{i}}-1$ 까지는 hidden state $z$가 고정된다.

HSMM의 많은 variant (HDP-HSMM, subHSMM)들이 있다.

이들은 state duration length에 임의의 분포를 갖는 것을 허용하였다.

---

HMM이나 HSMM은 latent space를 명시적으로 모델링할 수 있고 해석가능한 representation을 얻는 것은 가능한데, long-range temporal dependency를 잡는 데엔 한계가 있다.

3. Model

설명의 편의를 위해 single sequence에서의 모델을 나타내겠다.

Multiple sequence로의 확장은 바로 적용가능하다.

3.1 Generative Model

Long range temporal dependency와 segmentation을 모델링하기 위해, RNN과 HSMM을 결합하고자한다.

$$\begin{aligned} p_{\theta}\left(\mathbf{x}_{1: T}, z_{1: T}, d_{1: T}\right)=&p_{\theta}\left(\mathbf{x}_{1: T} \mid z_{1: T}, d_{1: T}\right) \cdot p_{\theta}\left(z_{1}\right) p_{\theta}\left(d_{1} \mid z_{1}\right) \\ &\prod_{t=2}^{T} p_{\theta}\left(z_{t} \mid z_{t-1}, d_{t-1}\right) p_{\theta}\left(d_{t} \mid z_{t}, d_{t-1}\right) \end{aligned}$$

Segmentation label $z_t$와 duration variable $d_t$는 categorical variable을 갖는다.

이들의 분포는

$$\begin{aligned} p_{\theta}\left(z_{t} \mid z_{t-1}, d_{t-1}\right)&=\left\{\begin{array}{ll} \mathbb{I}\left(z_{t}=z_{t-1}\right) & \text { if } d_{t-1}>1 \\ p_{\theta}\left(z_{t} \mid z_{t-1}\right) & \text { otherwise } \end{array}\right. \\ \\ p_{\theta}\left(d_{t} \mid z_{t}, d_{t-1}\right)&=\left\{\begin{array}{ll} \mathbb{I}\left(d_{t}=d_{t-1}-1\right) & \text { if } d_{t-1}>1 \\ p_{\theta}\left(d_{t} \mid z_{t}\right) & \text { otherwise } \end{array}\right. \end{aligned}$$

Transition probability에 대한 학습은 transition matrix 학습으로 구현된다.

---

Joint emission probability $p_{\theta}\left(\mathbf{x}_{1: T} \mid z_{1: T}, d_{1: T}\right)$는 segment 단위로 factorize 될 수 있다.

$i$번째 segment $\mathbf{x}_{s_{i}: s_{i}+d_{s_{i}}-1}$에 대한 factor는

$$\begin{aligned} p_{\theta}\left(\mathbf{x}_{s_{i}: s_{i}+d_{s_{i}}-1} \mid z_{s_{i}}, d_{s_{i}}\right)&=\prod_{t=s_{i}}^{s_{i}+d_{s_{i}}-1} p_{\theta}\left(\mathbf{x}_{t} \mid \mathbf{x}_{s_{i}: t-1}, z_{s_{i}}\right) \\ &=\prod_{t=s_{i}}^{s_{i}+d_{s_{i}}-1} p_{\theta}\left(\mathbf{x}_{t} \mid \mathbf{h}_{t}, z_{s_{i}}\right) \end{aligned}$$

$t$번째 observation $\mathbf{x}_{t}$의 분포는

$$p_{\theta}\left(\mathbf{x}_{t} \mid \mathbf{h}_{t}, z_{s_{i}}\right)=\mathcal{N}\left(x ; \boldsymbol{\mu}, \boldsymbol{\sigma}^{2}\right)$$

$\mathbf{h}_{t}$는 과거의 정보들을 담은 $\mathbf h_{t-1}$을 담기 때문에

• segment 안에서의 dependency뿐만 아니라
• segment들 간의 complex dependency를 모델링할 수 있다.

---

• $\mathbf{h}_{t}=\text{tanh}\left(\mathbf{W}_{x}^{\left(z_{s_{i}}\right)} \mathbf{x}_{t-1}+\mathbf{W}_{h}^{\left(z_{s_{i}}\right)} \mathbf{h}_{t-1}+\mathbf{b}_{h}^{\left(z_{s_{i}}\right)}\right)$
  • $\mathbf{W}_{x} \in \mathbb{R}^{K \times h \times m}$
  • $\mathbf{W}_{h}^{(z)} \in \mathbb{R}^{h \times h}$ for $z = 1, 2, \ldots ,K$
  • $\mathbf{b}_{h}^{(z)} \in \mathbb{R}^{h}$ for $z = 1, 2, \ldots ,K$
• $\boldsymbol{\mu}=\mathbf{W}_{\mu}^{\left(z_{s_{i}}\right)} \mathbf{h}_{t}+ \mathbf b_{\mu}^{\left(z_{s_{i}}\right)}$
  • $\mathbf{W}_{\mu}^{(z)} \in \mathbb{R}^{h \times m}$ for $z = 1, 2, \ldots ,K$
  • $\mathbf b_{\mu}^{(z)} \in \mathbb R^m $ for $z = 1, 2, \ldots ,K$
• $\log \boldsymbol{\sigma}^{2}=\mathbf{W}_{\sigma}^{\left(z_{s_{i}}\right)} \mathbf{h}_{t}+\mathbf{b}_{\sigma}^{\left(z_{s_{i}}\right)}$
  • $\mathbf{W}_{\sigma}^{(z)} \in \mathbb{R}^{h \times m}$ for $z = 1, 2, \ldots ,K$
  • $\mathbf b_{\sigma}^{(z)} \in \mathbb R^m $ for $z = 1, 2, \ldots ,K$

Generative model의 모든 parameter들은 $\theta$로 표현하겠다.

3.2 Structured Inference

Maximizing $\log p(\mathbf x)$는 posterior distribution이 일반적으로 intractable하기 때문에 EM 알고리즘으로 해결할 수 없다.

이에 대해서 최근의 Bayesian Learning에서의 method인 score function이나 SGVB는 tractable solution을 제공한다.

Score function은 높은 분산을 갖기에 상대적으로 분산이 작은 SGVB를 사용한다.

Marginal likelihood의 maximization은 ELBO의 maximization으로 이뤄진다.

$$\begin{aligned} \log p_{\theta}(\mathbf{x}) &\geq \mathcal{L}\left(\mathbf{x}_{1: T} ; \theta, \phi\right) \\ &=E_{q_{\phi}\left(z_{1: T}, d_{1: T} \mid \mathbf{x}_{1: T}\right)}\left[\log p_{\theta}\left(\mathbf{x}_{1: T}, z_{1: T}, d_{1: T}\right)-\log q_{\phi}\left(z_{1: T}, d_{1: T} \mid \mathbf{x}_{1: T}\right)\right] \end{aligned}$$

$\theta$는 generative network의 parameter를 나타내고

$\phi$는 inference network의 parameter를 나타낸다.

3.2.1 Bi-directional Inference

Posterior로의 informative approximation을 찾기 위해 bi-directional information으로 latent variable을 추론하게 된다.

의도를 이해하려면, Dai, 2017b, Krishnan et al., 2016, Fraccaro, 2016 는 읽어봐야 할 듯 하다.

아직 자세히 보진 않았지만, 실시간이 아닌 배치 단위로 posterior를 구하고자 하는 의도가 보인다.

그 경우에 posterior $p(\mathbf z_{t} \mid \mathbf x_{1:T})$에서의 D-separation을 통해 미래의 observation에 dependent하다는 것을 확인할 수 있다.

정확한 추론을 위해선, 역방향으로 가는 backward recurrent function $I_{t}$가 필요하다.

bi-directional information을 활용하는 논문 중에 대부분은 continuous variable에 집중을 했다.

$$\begin{aligned} q\left(z_{t} \mid d_{t-1}, I_{t} ; \phi\right) &=\operatorname{Cat}\left(\operatorname{softmax}\left(\mathbf{W}_{z}^{T} I_{t}\right)\right) \\ q\left(d_{t} \mid d_{t-1}, z_{t}, I_{t} ; \phi\right) &=\operatorname{Cat}\left(\operatorname{softmax}\left(\mathbf{W}_{d}^{T} I_{t}\right)\right) \end{aligned}$$

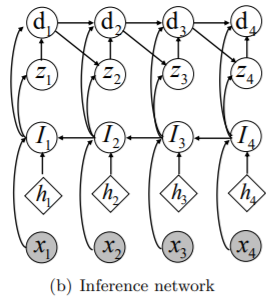
SGVB 알고리즘을 적용하기엔 categorical distributed latent variable이 reparameterizable하지 않기에 Gumbel-Softmax reparameterization trick을 사용한다.

3.2.2 Gumbel-Softmax Reparameterization

Skip

3.2.3 Algorithm

Let $F(z, d)=\log p_{\theta}\left(\mathbf{x}_{1: T}, z_{1: T}, d_{1: T}\right)-\log q\left(z_{1: T}, d_{1: T} \mid \mathbf{x}_{1: T}\right)$

$z$와 $d$가 Gumbel-Softmax로 대체된 것을 $\tilde{F}(y, g)$로 표기하자.

$$\mathcal{L}\left(\mathbf{x}_{1: T} ; \theta, \phi\right) \approx E_{y \sim \operatorname{Concrete}(\boldsymbol{\pi}(t), \tau)}[\tilde{F}(y, g)]=E_{g \sim \Pi_{N} \operatorname{Gumbel}(0,1)}[\tilde{F}(y, g)]$$

Approximated ELBO는 SGVB estimator로 근사가 가능하다.

$$\begin{aligned} \frac{\partial}{\partial \phi} E_{g \sim \prod_{N} \operatorname{Gumbel}(0,1)}[\tilde{F}(y, g)] &=E_{g \sim \prod_{N} \operatorname{Gumbel}(0,1)}\left[\frac{\partial}{\partial \phi}(\tilde{F}(y, g))\right] \\ &\approx \frac{1}{B} \sum_{b=1}^{B} \frac{\partial}{\partial \phi}\left(\tilde{F}\left(y^{b}, g^{b}\right)\right), \quad g^{b}:=\left(g_{1}^{b}, \ldots, g_{N}^{b}\right) \end{aligned}$$

4. Related Work

SSM과 RNN을 결합한 generative sequential data modeling 연구들을 리뷰하겠다.

• Krishnan, 2015은 linear dynamical system에서 VAE와 continuous SSM을 결합했다.
• Krishnan, 2016은 future & past hidden variable을 동시에 condition을 건 inference network를 제안했다.
• Johnson, 2016은 structured inference를 위해 일반적인 emission density를 채택했다..?
• Fraccaro, 2016은 RNN에 stochastic latent variables를 결합하여 SSM을 확장하였다.

HDTS에서의 segmentation을 위해 우리의 논문은 SSM part를 discrete latent variable로 구현하였다.

---

이의 학습을 위해 variational inference with discrete latent variable의 연구들이 있다.

• Bayer and Osendorfer, 2014는 RNN 구조의 discrete latent variable을 score function으로 학습했다.
• Mnih and Rezende (2016)도 score function으로 학습을 하였으나 이의 분산을 줄이기 위해 neural baseline을 도입하였다.

---

Linearizing intractable term을 활용한 최적화 테크닉도 있다.

이부분은 잘 모름

Amortized inference 방식으로 학습할 수 있는 Gumbel-Softmax distribution이 등장했다.

5. Experiment

SSNN을 여러 상황에서 평가한다.

5.1 Synthetic Experiment

Pendulum dynamics는 각도와 각속도에 의해 설명된다.

$$m l^{2} \frac{d^{2} \phi(t)}{d t^{2}}=-\mu \frac{d \phi(t)}{d t}+m g l \sin \phi(t)+u(t) .$$

펜듈럼의 이미지 sequence들을 데이터셋으로 활용하여 학습했다.

다음 observation은 단순히 이전의 각도에만 의존하는 것이 아닌 각속도에도 의존하는 복잡한 dependency를 갖는다.

각도와 각속도에 대한 예측을 잘하는 것을 보아 제안하는 SSNN은 복잡한 dependency를 이해할 수 있는 능력이 있다.

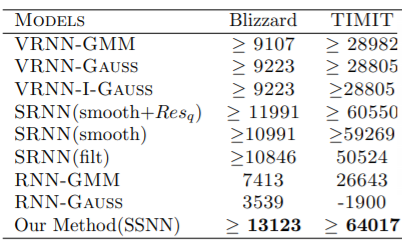
5.2 Speech modeling

VRNN에서 이미 설명을 하여서 생략하겠다.

5.3 Segmentation and Labeling of Time Series

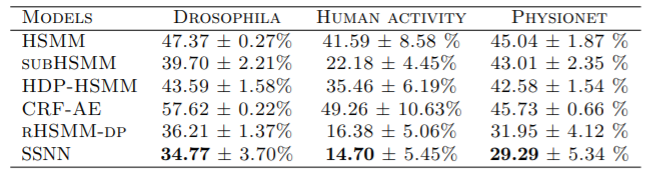
SSNN over HSMM이 HDTS에서 segmentation할 때 이점이 있다는 것을 보이기 위해

• Human activity
• Drosophila dataset
• PhysioNet

의 데이터셋을 활용하였다.

---

Human activity는 스마트폰에서 수집한 신호로 이루어져있다.

각 사람들은 12개의 활동을 하게 된다.

기록된 sequence는 61개이고 최대 3000 time-step을 갖는다.

$\mathbf x_t$는 6차원 벡터이다.

---

Drosophila는 초파리의 다리의 움직임에 대한 시계열 데이터이다.

$\mathbf x_t$는 45차원이다.

최대 time-step은 10000이다.

GS distribution의 temperature는 0.0001로 고정하였다.

---

PhysioNet은 4가지의 상태중 하나이다.

GS distribution의 temperature는 0.15에서 시작해서 0.0001로 줄여나갔다.

---

Accuracy를 재는 데에는 ground truth와 predicted segments를 비교하였다.