0. Abstract

Intelligent agent는 (무엇을 볼(see) 수 있는 지, 어떤 action을 할(do) 수 있는 지) 에 기반해, policy optimization을 하게 된다.

대부분의 policy는 $see \times do \rightarrow \mathcal [0,1]$의 함수로 parameterized 될 수 있고 이 논문에선 이를 mixed policy라고 부르겠다.

이 논문에선 mixed policy의 특징을 조사한다.

그 다음에,

불필요한 action들을 identify하는 graphical criterion을 도입하여 non-redundancy을 이끌어 낸 다음에
Optimal policy의 충분조건을 도출한다.

Causal characterization은 standard approach를 따르는 agent가 매력이 떨어지고 optimal performance에 도달하지 못한다는 결론을 내린다.

1. Introduction

대량의 정보를 받는 complex environment에서 agent가 (safe, efficient, rational)하게 동작하길 기대한다.

CI의 discipline은 complex environment에서 structural invariance를 알아내고자 하는 툴을 제공한다.

Causal mechanism이 충분히 이해됐을 땐, agent는 정교한 intervention을 디자인하여 요구되는 policy를 가져올 수 있다.

ML 분야에서, RL과 bandits은 특정 목표에 도달할 수 있도록 에이전트들을 설계하는 프레임워크를 제공한다.

RL과 CI을 엮는 연구가 최근 커지고 있다.

최근 [9-11]에서 causal knowledge를 sequential decision making에 적용하여 성능 향상을 이끌어내는 식으로 명시적으로 RL과 CI를 연관지었다.

RL과는 따로 떨어져서, CI 연구자들은 sequential decision making을 dynamic treatment regime으로 해석하여 CE identification from observational data 문제로 연구해오고 있었다.[22-27]

DM의 주된 task중에 하나는 policy의 parameter를 최적화하는 것이다.

Policy의 action set과 context set이 미리 명시된다는 관점에서, policy의 scope는 보통 고정됐다.

하지만 Causal understang은 scope들을 고르는 기준을 제시한다.

Scope가 고정되지 않았다는 관점에서 mixed policy라고 부른다.

이 논문에선 mixed policy를 갖고 SDM을 하게 된다.

구체적인 예시를 들기 위해, 아래의 environment $G$에서의 agent를 고려해보자.

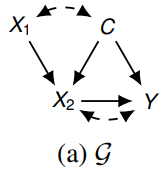
$C$ : context variable
$\mathbf{X}=\left\{X_{1}, X_{2}\right\}$ : action variables
$Y$ : reward variable

Agent의 목표는 reward $\mu_{\boldsymbol{\pi}} \doteq \mathbb{E}_{\boldsymbol{\pi}}[Y]$를 최대화 하는 것이다.

Mixed policy scope(MPS)는 policy가 intervene하는 action 변수들과 action 결정에 고려한 변수들로 정의된다.

standard contextual bandit(CB)는 policy $\boldsymbol{\pi}_{\mathrm{CB}} = \left\{\pi\left(x_{1} \mid c\right), \pi\left(x_{2} \mid x_{1}, c\right)\right\}$를 최적화한다.

일반적으로, policy는 이미 정해진 MPS로 charcterize되는 policy space $\boldsymbol{\Pi}_{\mathrm{CB}}$에서 최적화된다.

불행히도, $\boldsymbol \pi_{\mathrm{CB}}^{*} \doteq \arg \max _{\boldsymbol{\pi} \in \boldsymbol \Pi_{\mathrm{CB}}} \mu_{\boldsymbol{\pi}}$는 suboptimal일 수 있다.

Let $X_1, X_2, C, Y$ be binary random variables.

Let $U_1$ and $U_2$ be fair coins. ; $U_1 (U_2)$은 $X_1(X_2)$에 연결된 confounder이다.

Let $\epsilon$ be a noise over $X_1$ with $P(\epsilon=1) = 0.2$

Let $\oplus$ be exclusive-or operator and $\vee$ be or operator and

$X_{1} \leftarrow U_{1} \oplus \epsilon$
$C \leftarrow U_{1}$
$X_{2} \leftarrow U_{2} \oplus X_{1} \oplus C$
$Y \leftarrow\left(1-\left(X_{2} \oplus U_{2}\right)\right) \vee C$

Since the policy $\boldsymbol \pi _{CB}$ determines $X_2$ irrelevant to $U_2$, $\mu_{\mathcal{S}_{\mathrm{CB}}}^{*}=0.75$

계산해봤을 때, 아무런 policy가 없을 때의 reward가 0.9였다.

반면에, $X_2$는 intervene하지 않고 $X_1 = C$만 intervene 하였을 때, optimal expected reward가 1로 나온다.

이 환경에서, 15개의 MPS가 존재한다.

MPS들은 non-redundancy와 optimality로 구분될 수 있다.

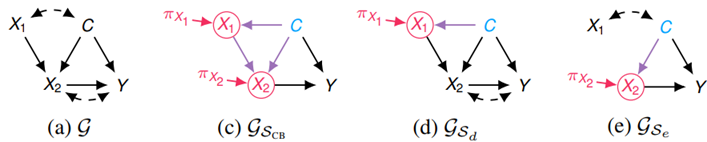
Let

$\mathcal S_{a}=\{\}$
$\mathcal{S}_{\mathrm{CB}}=\left\{\left\langle X_{1},\{C\}\right\rangle,\left\langle X_{2},\left\{X_{1}, C\right\}\right\rangle\right\}$
$\mathcal{S}_{d}=\left\{\left\langle X_{1},\{C\}\right\rangle\right\}$
$\mathcal{S}_{e}=\left\{\left\langle X_{2},\{C\}\right\rangle\right\}$

$\subset$ 표현은 scope의 action set과 context set을 의미하고 $\leq$ 표현은 scope의 optimal reward에 대한 비교이다.

Optimal reward에 대한 비교가 없는 건 environment에 따라 우위가 다르다를 의미

Non-redundancy는 scope에서 action이나 context를 빼는게 안좋은 영향을 주는 지 여부이다.

예를 들어, $\mathcal{S} \supsetneq \mathcal{S}^{\prime}$ 인데, $\mathcal{S}={ }_{\mu} \mathcal{S}^{\prime}$ 면, $S$는 redundant하다.

결국, CB agent는 불필요한 $X_2$ action을 하느라 자원을 낭비하는 중이다.

Optimality of scope $S$는 어떤 environment에서든 $S$보다 더 나은 scope는 없다를 의미한다.

모든 environment에 대해서 부등식이 유지가 안된다면 scope간의 비교는 불가능하다.

$S_d$와 $S_e$만 non-redundancy와 optimality를 만족한다.

이는 곧 agent는 조심스럽게 context와 action variable을 골라야함을 의미한다.

Contributions

Non-redundancy와 Optimality에 대한 결과들이 policy의 exploration의 근간을 제공한다고 기대한다.

Standard approach를 따르는 agent는 optimal performance에 도달할 수 없다.

Notation

$\dot{\cup}$ : union of two disjoint sets
$X \rightarrow Y$ : $X$ is an argument of $f_Y$ in $\mathcal G$
$X \leftrightarrow Y$ : $\mathbf{U}_{\mathbf{w}} \perp \mathbf{U}_{X} \text { and } \mathbf{U}_{Y} \not \subset \mathbf{U}_{\mathbf{W}} \quad $ where $\mathbf W$ is a maximal subset in $\mathbf{V} \backslash\{X\}$
- ??
$\mathcal{G}\left\langle\mathbf{V}^{\prime}\right\rangle$ : latent projection of $G$ onto $V’$
- $G_{V’}$과 다른 것이 무엇일까?, latent projection?
$C h, P a, A n, D e$ : 는 argument를 포함한다.
$ch, pa, an, de$ : 는 argument를 포함하지 않는다.

[29, 30]은 agent가 $G$를 모르더라도 agent가 학습을 위해 active intervention을 하는 논문

2. Mixed Policies: Fundamentals & Basic Results

Causal understanding은 다양한 scope를 갖는 policy spcae들 사이에서 scope의 종류는 고르는 데에 도움을 준다.

Definition 1 (MPS)

Let $G$ be a causal graph.

Let $Y$ be a specific reward variable.

Let $\mathbf{X}^{\star} \subseteq \mathbf{V} \setminus \{Y\}$ be a set of intervenable variables.

Let $\mathbf{C}^{\star} \subseteq \mathbf{V} \setminus \{Y\}$ be a set of contextual variables.

A mixed policy scope $S$ is defined as a collection of pairs $\left\langle X, \mathbf{C}_{X}\right\rangle$ for each $X \in \mathbf X^\star, \mathbf C_X \subseteq \mathbf C^\star\setminus \{X \}$

And, $G_S$ is acyclic.

$G_S$는 기존 $G$에서 $X$로 들어오는 edge들을 $\mathbf C_X$로 대체하는 것이다.

$\mathcal S_{a}=\{\}$
$\mathcal{S}_{\mathrm{CB}}=\left\{\left\langle X_{1},\{C\}\right\rangle,\left\langle X_{2},\left\{X_{1}, C\right\}\right\rangle\right\}$
$\mathcal{S}_{d}=\left\{\left\langle X_{1},\{C\}\right\rangle\right\}$
$\mathcal{S}_{e}=\left\{\left\langle X_{2},\{C\}\right\rangle\right\}$

Definition 2 (MP)

Given $\left\langle\mathcal{G}, Y, \mathbf{X}^{\star}, \mathbf{C}^{\star}\right\rangle$ & SCM $\mathcal{M} \sim \mathcal{G}$ with $\mathfrak{X}_{Y} \subseteq \mathbb{R}$,

a mixed policy $\boldsymbol \pi$ is a realization of a mixed policy scope.

$\mathfrak X$은 support를 의미한다.

Formally, $\boldsymbol{\pi} \doteq\left\{\pi_{X \mid \mathbf{C}_{X}}\right\}_{\left\langle X, \mathbf{C}_{X}\right\rangle \in \mathcal{S}}$ where $\pi_{X \mid \mathbf{C}_{X}}: \mathfrak{X}_{X} \times \mathfrak{X}_{\mathbf{C}_{X}} \mapsto[0,1]$

이전 예제의 MPS $S_{CB}$의 mixed policy $\pi$는 $\left\{\pi_{X_{1} \mid\{C\}}, \pi_{X_{2} \mid\left\{C, X_{1}\right\}}\right\}$이다.

가독성을 위해, $\left\{\pi\left(x_{1} \mid c\right), \pi\left(x_{2} \mid x_{1}, c\right)\right\}$ 라고 쓰겠다.

Environemnt SCM $\mathcal M$이 주어졌을 때, mixed policy $\boldsymbol \pi$는 수정된 SCM $\mathcal{M}_{\boldsymbol \pi}$를 유도한다.

$\mathcal{M}_{\boldsymbol \pi}$ : $\text{for each } X \in \mathbf X(\mathbf \pi), \quad f_X \text{ is replaced by} \quad \pi_{X \mid \mathbf{C}_{X}}$
Let $P_{\boldsymbol{\pi}}$ denote the joint distribution over the variables from $\mathcal M_{\pi}$

Expected Reward

Let

intervened variables $\mathbf{X}(\mathcal{S}) \doteq\left\{X \mid\left\langle X, \mathbf{C}_{X}\right\rangle \in \mathcal{S}\right\}$
active contexts $\mathbf{C}(\mathcal{S}) \doteq \bigcup_{X \in \mathbf{X}(\mathcal{S})} \mathbf{C}_{X}$
If $\boldsymbol{\pi} \sim \mathcal{S}$,
- $\mathbf{X}(\boldsymbol{\pi}) \doteq \mathbf{X}(\mathcal{S})$
- $\mathbf{C}(\boldsymbol{\pi}) \doteq \mathbf{C}(\mathcal{S})$
$\mathbf{C}^{-}=\mathbf{C}(\boldsymbol{\pi}) \setminus\mathbf{X}(\boldsymbol{\pi})$

Then, expected reward for $\boldsymbol \pi$ can be expressed as

$\begin{aligned} \mu_{\boldsymbol{\pi}} &= \sum_{y, \mathbf{x}, \mathbf{c}^{-}} y P_{\boldsymbol \pi}(y, \mathbf{x}, \mathbf{c}^{-}) \\&=\sum_{y, \mathbf{x}, \mathbf{c}^{-}} y P_{\mathbf{x}}\left(y, \mathbf{c}^{-}\right) \prod_{X \in \mathbf{X}(\boldsymbol{\pi})} \pi\left(x \mid \mathbf{c}_{x}\right) \\ &= \sum_{y, \mathbf{x}^{\prime}, \mathbf{c}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y, \mathbf{c}^{\prime}\right) \prod_{X \in \mathbf{X}^{\prime}} \pi\left(x \mid \mathbf{c}_{x}\right) \\ \text{where }\mathbf{X}^{\prime}& \subseteq \mathbf{X}(\boldsymbol{\pi}) \quad \text{ and } \quad \mathbf{C}^{\prime}=\bigcup_{X \in \mathbf{X}^{\prime}} \mathbf{C}_{X} \setminus \mathbf{X}^{\prime} \quad \text{and } \quad Q^{\prime}=P_{\boldsymbol{\pi} \setminus \mathbf{X}^{\prime}} \end{aligned}$

마지막 표현식은 보고자 하는 action variable $\mathbf X’$에 집중할 때의 표현식이다.

$P_{\boldsymbol \pi}$는 (context, action, reward)의 joint distribution이다.

$Q_{\mathbf{x}^{\prime}}^{\prime}\left(y, \mathbf{c}^{\prime}\right)$는 action $\mathbf X’$이 intervene 되었을 때, (reward, context $\mathbf C’$)의 joint distribution이다.

${\boldsymbol{\pi} \setminus \mathbf{X}^{\prime}} $ 는 policy에서 $\mathbf{X}^{\prime}$에 대한 건 뺀 것이다.

Optimality and deterministic mixed policy

Given an environment, mixed policy $\boldsymbol \pi$ is said to be optimal if $\mu_{\boldsymbol{\pi}}=\mu^{*} \doteq \max _{\boldsymbol{\pi}^{\prime} \in \boldsymbol{\Pi}} \mu_{\boldsymbol{\pi}^{\prime}}$

Let $\boldsymbol{\Pi}_{\mathcal{S}} \doteq\{\boldsymbol{\pi} \in \boldsymbol{\Pi} \mid \boldsymbol{\pi} \sim \mathcal{S}\}$

$\boldsymbol \pi \in \boldsymbol \Pi_{\mathcal S}$ is optimal w.r.t. $\mathcal S$ if $ \mu _{\boldsymbol \pi} = \mu_{\mathcal{S}}^{*} \doteq \max _{\boldsymbol{\pi}^{\prime} \in \boldsymbol{\Pi}_{\mathcal{S}}} \mu_{\boldsymbol{\pi}^{\prime}}$

Proposition 1

Given a MPS $\mathcal S$, ${}^{\exists} \boldsymbol \pi \in \boldsymbol \Pi_{\mathcal S}$ s.t.

deterministic
optimal w.r.t. $\mathcal S$

See [36-39]…

Proposition 2 (Separation of Actions and Contexts)

Given an MPS $\mathcal S$, $^{\exists}$deterministic $\boldsymbol{\pi} \in \boldsymbol{\Pi}$ s.t.

$\mathbf{X}(\boldsymbol{\pi}), \mathbf{C}(\boldsymbol{\pi})$ are disjoint
$\mu_{\boldsymbol{\pi}}=\mu_{\mathcal{S}}^{*}$

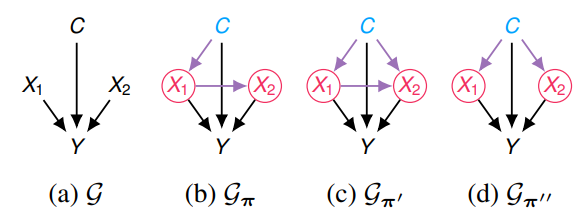
Proposition 2는 $X_2$의 context에 $C$만 고려해도 된다는 것을 의미한다.

3. Non-redundant Mixed Policy

MP 최적화는 agent가 불필요한 action/context를 intervene/observe 하는 것을 피하도록 MPS의 효율성에 대한 평가를 포함한다.

Let $\mathcal{S}^{\prime}\subseteq {S}$ so that

$\mathbf{X}\left(\mathcal{S}^{\prime}\right) \subseteq \mathbf{X}(\mathcal{S})$ and
$\mathbf{C}_{X}^{\prime} \subseteq \mathbf{C}_{X}$ for every $\left\langle X, \mathbf{C}_{X}^{\prime}\right\rangle \in \mathcal{S}^{\prime}$

Let $\boldsymbol{\pi}^{\prime} \sim \mathcal{S}^{\prime}$ and $\boldsymbol \pi \sim \mathcal{S}$

Then, $\boldsymbol \pi^{\prime} \subseteq \boldsymbol\pi$ means

$\pi^{\prime}\left(x \mid \mathbf{c}_{x}^{\prime}\right)=\sum_{\mathbf{c}_{x}^{\prime \prime}} \pi\left(x \mid \mathbf{c}_{x}\right) P_{\boldsymbol{\pi}}\left(\mathbf{c}_{x}^{\prime \prime} \mid \mathbf{c}_{x}^{\prime}\right) \quad \text{for every $X \in \mathbf{X}\left(\mathcal{S}^{\prime}\right)$}$
where $\mathbf{C}_{X}^{\prime \prime}=\mathbf{C}_{X} \setminus\mathbf{C}_{X}^{\prime}$

Definition 3

Given $\left\langle\mathcal{G}, Y, \mathbf{X}^{\star}, \mathbf{C}^{\star}\right\rangle$, MPS is said to be non-redundant if

$^{\exists}\text{SCM $\mathcal{M} \sim \mathcal{G}$ $\quad$&$\quad $ $^{\exists}$$\boldsymbol{\pi} \sim(\mathcal{S}, \mathcal{M})\quad $ s.t. } \mu_{\boldsymbol{\pi}} \neq \mu_{\boldsymbol{\pi}^{\prime}} \text{ for every $\boldsymbol \pi^{\prime} \subsetneq \boldsymbol \pi$}$

$\boldsymbol \pi^{\prime} \subseteq \boldsymbol\pi$는 각 $X$별로 context가 이미 주어졌을 때, context를 조금만 취해도 기존 $\boldsymbol \pi$와 똑같은 $\boldsymbol \pi’$를 지칭한다.

해석 : 특정 SCM에서는, 특정 $\boldsymbol \pi$를 따라하려는 $\boldsymbol \pi’$들이 reward만큼은 따라가지 못한다.

Theorem 1

Let $\mathcal{S}=\left\{\left\langle X, \mathbf{C}_{X}\right\rangle\right\}_{X \in \mathbf{X}}$ be an MPS

Let $\mathcal{H}=\mathcal{G}_{\mathcal{S}}$.

$\mathcal S$ is non-redundant iff

${}^\forall X \in \mathbf{X}$ satisfies $ X \in\operatorname{an}(Y)_{\mathcal{H}}$

and
Given $X \in \mathbf{X}$, $^{\forall}C \in \mathbf{C}_{X}$ satisfies $C \not \perp Y \mid \mathbf{C}_{X} \setminus\{C\} \quad \text { in } \mathcal{H} \backslash\{X\}$

직감적으로 말하면, 필요없는 $X$가 있으면 안되고 &

$X$의 부모인 $C$는$X$를 거치지 않은 $Y$로의 open path가 존재한다.

==> (1)

Assume $^{\exists}X \in \mathbf X$ s.t. $X \in \mathbf{X} \setminus an(Y)_{\mathcal{H}}$

Let $Q^{\prime}=P_{\boldsymbol{\pi} \setminus\{X\}}$

Let $\mathcal{H}^{\prime}=\mathcal{G}_{\boldsymbol{\pi} \setminus\{X\}}$

$\mathcal{G}_{\boldsymbol{\pi} \setminus\{X\}}$는 기존의 $\mathcal{G}$에서 $X$에 대해선 그대로 내비둔 SCM을 의미한다.

Intervention을 하든($\mathcal H$) 안하든($\mathcal H’$) $X$의 자손에 $Y$가 없다는 사실은 변하지 않기에,

$X \in \mathbf{X} \backslash \operatorname{an}(Y)_{\mathcal{H}^{\prime}}$

Since $\left(X \perp Y \mid \mathbf{C}_{X}\right) \text { in } \mathcal{H}^{\prime}_{\overline{X\left(\mathbf{C}_{X}\right)}}=\mathcal{H}_{\bar{X}}^{\prime}$, (Rule 3)

$Q_{x}^{\prime}\left(y \mid \mathbf{c}_{x}\right)=Q^{\prime}\left(y \mid \mathbf{c}_{x}\right)$

Since $X \perp \mathbf{C}_{X} \text { in } \mathcal{H}_{\bar{X}}^{\prime}$, (Rule 3)

$Q_{x}^{\prime}\left(\mathbf{c}_{x}\right)=Q^{\prime}\left(\mathbf{c}_{x}\right)$

Then,

$\begin{aligned} \mu_{\boldsymbol{\pi}} &=\sum_{y, x, \mathbf{c}_{x}} y Q_{x}^{\prime}\left(y, \mathbf{c}_{x}\right) \pi\left(x \mid \mathbf{c}_{x}\right) \\ &=\sum_{y, x, \mathbf{c}_{x}} y Q_{x}^{\prime}\left(y \mid \mathbf{c}_{x}\right) Q_{x}^{\prime}\left(\mathbf{c}_{x}\right) \pi\left(x \mid \mathbf{c}_{x}\right) \\ &=\sum_{y, x, \mathbf{c}_{x}} y Q^{\prime}\left(y \mid \mathbf{c}_{x}\right) Q^{\prime}\left(\mathbf{c}_{x}\right) \pi\left(x \mid \mathbf{c}_{x}\right) \\ &=\sum_{y, x, \mathbf{c}_{x}} y Q^{\prime}\left(y, \mathbf{c}_{x}\right) \pi\left(x \mid \mathbf{c}_{x}\right) \\ &=\sum_{y, \mathbf{c}_{x}} y Q^{\prime}\left(y, \mathbf{c}_{x}\right) \sum_{x} \pi\left(x \mid \mathbf{c}_{x}\right) \\ &=\sum_{y} y Q^{\prime}(y) \\ &=\mu_{\boldsymbol{\pi} \setminus\{X\}} \end{aligned}$

It contradicts to “$\mathcal S$ is non-redundant”

==> (2)

Assume $^{\exists}C \in \mathbf C_X$ s.t. $C \perp Y \mid \mathbf{C}_{X}^- \quad \text { in } \mathcal{H} \backslash\{X\}\quad $ where $\mathbf{C}_{X}^- = \mathbf{C}_{X} \setminus\{C\}$

Let $Q=P_{\boldsymbol{\pi}}$ and $Q^{\prime}=P_{\boldsymbol{\pi} \setminus\{X\}}$ for some $\boldsymbol{\pi} \sim \mathcal{S}$

Note that $\mathcal{H} \setminus \{X\} = \mathcal{H}^{\prime} \setminus\{X\}$ because the difference btw $\mathcal H \& \mathcal H^{\prime}$ is $pa(X)_{\mathcal H} \neq pa(X)_{\mathcal H ^{\prime}}$

$\begin{aligned} \mu_{\boldsymbol{\pi}} &=\sum_{y, x, \mathbf{c}_{x}} y Q_{x}^{\prime}\left(y \mid \mathbf{c}_{x}\right) Q_{x}^{\prime}\left(\mathbf{c}_{x}\right) \pi\left(x \mid \mathbf{c}_{x}\right) \quad &\because \text{def}\\ &=\sum_{y, x, \mathbf{c}_{x}} y Q_{x}^{\prime}\left(y \mid \mathbf{c}_{x}^{-}\right) Q_{x}^{\prime}\left(\mathbf{c}_{x}\right) \pi\left(x \mid \mathbf{c}_{x}\right) \quad &\because \text{assumption; Rule1} \\ &=\sum_{y, x, \mathbf{c}_{x}} y Q_{x}^{\prime}\left(y \mid \mathbf{c}_{x}^{-}\right) Q_{x}^{\prime}\left(\mathbf{c}_{x}^{-}\right)Q_{x}^{\prime}\left(c \mid \mathbf{c}_{x}^{-}\right) \pi\left(x \mid \mathbf{c}_{x}\right) \\ &=\sum_{y, x, \mathbf{c}_{x}^{-}} y Q_{x}^{\prime}\left(y, \mathbf{c}_{x}^{-}\right) \sum_{c} Q_{x}^{\prime}\left(c \mid \mathbf{c}_{x}^{-}\right) \pi\left(x \mid \mathbf{c}_{x}\right) \\ &=\sum_{y, x, \mathbf{c}_{x}^{-}} y Q_{x}^{\prime}\left(y, \mathbf{c}_{x}^{-}\right) \sum_{c} Q_{x}\left(c \mid \mathbf{c}_{x}^{-}\right) \pi\left(x \mid \mathbf{c}_{x}\right) \quad &\because \text{$Q$ and $Q'$ is same w/o $X$} \\ &=\sum_{y, x, \mathbf{c}_{x}^{-}} y Q_{x}^{\prime}\left(y, \mathbf{c}_{x}^{-}\right) \sum_{c} P_{\boldsymbol \pi}\left(c \mid \mathbf{c}_{x}^{-}\right) \pi\left(x \mid \mathbf{c}_{x}\right) \quad &\because C\perp_\overline{\mathcal H(\mathbf C_x^-) } X \mid \mathbf C^-_{\mathbf x}\text{; MPS def ; Rule3} \\ &=\sum_{y, x, \mathbf{c}_{x}^{-}} y Q_{x}^{\prime}\left(y, \mathbf{c}_{x}^{-}\right) \pi^{\prime \prime}\left(x \mid \mathbf{c}_{x}^{-}\right) \quad &\text{where } \pi^{\prime \prime}\left(x \mid \mathbf{c}_{x}^{-}\right) \doteq \sum_{c} P_{\boldsymbol{\pi}}\left(c \mid \mathbf{c}_{x}^{-}\right) \pi\left(x \mid \mathbf{c}_{x}^{-}, c\right) \\ &=\mu_{\boldsymbol{\pi}^{\prime \prime}} \end{aligned}$

It contradicts to “$\mathcal S$ is non-redundant”

<==

여기 증명은 이해하기 어려워서 일단 생략

3.1 Non-Redundancy under Optimality

주어진 SCM 하에서, 임의의 $\boldsymbol \pi$에 대해 Non-Redeundancy는 MPS의 context가 적절한 지 여부를 판단함에 있어서 불충분하다.

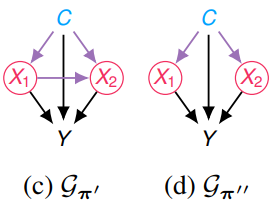
Proposition 2에서 (c)의 경우 $X_2$ context를 줄이면서 똑같은 optimal reward를 주는 policy가 있음을 암시했다.

하지만 NR은 (c)를 거르지 못한다.

그리고 관심의 대상은 일반적으로 임의의 $\boldsymbol \pi$가 아니라 optimal policy w.r.t. $\mathcal S$에서의 non-redundancy일 것이다.

Definition 4 (Non-Redundacy under Optimality)

Given $\left\langle\mathcal{G}, Y, \mathbf{X}^{\star}, \mathbf{C}^{\star}\right\rangle$, MPS is said to be non-redundant under optimality if

$^{\exists}\text{SCM $\mathcal{M} \sim \mathcal{G}$ $\quad$ s.t. } u_{\mathcal{S}}^{*}>\mu_{\mathcal{S}^{\prime}}^{*} \text{ for every $\mathcal{S}^{\prime} \subsetneq \mathcal{S}$}$

Optimality하에서, 임의의 action set $\mathbf{X}^{\prime} \subseteq \mathbf{X}^{\star}$에 대해, context set $\mathbf{C}^{\prime} \subsetneq \mathbf{C}_{\mathbf{X}^{\prime}} \backslash \mathbf{X}^{\prime}$이 쓸모있는가에 대한 criterion을 알아보자.

Proposition 3

Given a MPS $\mathcal S$ and its optimal mixed policy $\boldsymbol{\pi} \sim \mathcal{S}$ ,

Let $\mathbf{X}^{\prime} \subseteq \mathbf{X}(\mathcal{S})$ and $\mathbf{C}^{\prime} \subsetneq \mathbf{C}_{\mathbf{X}^{\prime}} \backslash \mathbf{X}^{\prime}$

Let $Q^{\prime}=P_{\boldsymbol{\pi} \backslash \mathbf{X}^{\prime}}$

$\begin{aligned} \text{if } ^{\exists} & \text{decision rules } \left\{\pi^{\prime}\left(x \mid\left(\mathbf{x}^{\prime} \dot{\cup} \mathbf{c}^{\prime}\right) \cap \mathbf{c}_{x}\right)\right\}_{X \in \mathbf{X}^{\prime}} \text{ s.t. } \mu_{\mathcal{S}}^{*}=\sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y, \mathbf{c}^{\prime}\right) \prod_{X \in \mathbf{X}^{\prime}} \pi^{\prime}\left(x \mid\left(\mathbf{x}^{\prime} \dot{\cup} \mathbf{c}^{\prime}\right) \cap \mathbf{c}_{x}\right) \\ \\ \\ &\text{, then } \\ &1. \quad \mathbf{C}_{\mathbf{X}^{\prime}} \backslash\left(\mathbf{C}^{\prime} \bigcup \mathbf{X}^{\prime}\right) \text{ are jointly redundant to $\mathbf{X}^{\prime}$ under optimality} \\ &2. \quad \mathcal{S}^{\prime} \doteq\left(\mathcal{S} \backslash \mathbf{X}^{\prime}\right) \cup \left\{ \left\langle X, \mathbf{C}^{\prime} \cap \mathbf C_X \right\rangle \right\}_{X\in \mathbf X^{\prime}} \text{ satisfies } \mu_{\mathcal{S}}^{*}=\mu_{\mathcal{S}^{\prime}}^{*} \end{aligned}$

관심있는 action set에서, 그의 context를 덜 써도 optimal reward를 따라갈 수 있는 policy가 있다면 나머지 context는 redundant하다.

Proposition 3의 condition을 sufficient graphical criterion으로 쉽게 다룰 수도 있다.

Theorem 1의 대우를 취하면,
- $C$ is redundant to $X$ iff $C \perp Y \mid \mathbf{C}_{X} \setminus\{C\} \quad \text { in } \mathcal{H} \backslash\{X\}$

중복을 제거하면, $\mathbf{C}_{X} \setminus\{C\}$로 막히는 path뿐만 아니라, $Y \leftarrow \cdots \leftarrow X^{other} \rightarrow C$도 막힐 수 있다.
common cause를 갖던 $X^{other}$를 통한 path가 막힐 수 있음을 체계적으로 고려하기 위해 implied variable을 도입하겠다.

Let $\lceil\mathbf{Z}\rceil$ be the implied variable w.r.t. conditionals $\mathbf Z$ which is computed as

$\begin{aligned} 0.& \lceil\mathbf{Z}\rceil \leftarrow \mathbf{Z} \\ 1.& \lceil\mathbf{Z}\rceil \leftarrow\lceil\mathbf{Z}\rceil \cup\left\{X \in \mathbf{X}(\mathcal{S}) \mid \mathbf{C}_{X} \subseteq\lceil\mathbf{Z}\rceil\right\} \\ 2.& \text{repeat 1 until convergence} \end{aligned}$

Then, given determiistic (& optimal) $\boldsymbol{\pi} \sim \mathcal{S}$,

$\mathbf{W} \perp \mathbf{T} \mid \mathbf{Z} \text{ for } P_{\boldsymbol{\pi}} \quad \Leftrightarrow \quad \mathbf{W} \perp \mathbf{T} \mid\lceil\mathbf{Z}\rceil \text { in } \mathcal{G}_{\boldsymbol{\pi}}$

Consider $C \in \mathbf C_X$ for some $X \in \mathbf X (\boldsymbol \pi )$

The redundancy of a single context canbe expressed as $\left(C \perp Y \mid\left\lceil\mathbf{C}_{X} \backslash\{C\}\right\rceil\right)_{\mathcal{H} \backslash\{X\}}$

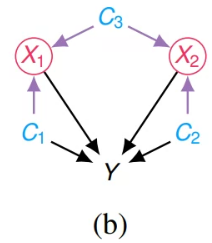
예시1 (sufficient graphical criterion)

$\left(C_2 \perp Y \mid\left\lceil\mathbf{C}_{X_2} \backslash\{C_2\}\right\rceil\right)_{\mathcal{H} \backslash\{X_2\}} = \left(C_2 \perp Y \mid\left \{C_1, X_1\right\}\right)_{\mathcal{H} \backslash\{X_2\}}$
$C_2$가 믿고있었던 $X_2$를 걸치지 않은 backdoor path $C_{2} \leftarrow X_{1} \rightarrow Y$는 사라지는 꼴이다.
결국, $C_2$를 $\mathbf C_{X_2}$에서 제거해도 된다.

예시2 $C_3$는 $\mathbf X = \{ X_1, X_2\}$에 의해 막힌다

$X_1$과 $X_2$는 $C_3$를 context로 사용한다.
$\mu_{\boldsymbol{\pi}}=\mathbb{E}_{c_{3}}\left[\mathbb{E}_{\boldsymbol{\pi}}\left[y \mid c_{3}\right]\right]$
Let $c_{3}^{*}=\arg \max _{c_{3} \in \mathfrak{X}_{C_{3}}} \mathbb{E}_{\boldsymbol{\pi}}\left[y \mid c_{3}\right]$
Then, $\pi^{\prime}\left(x_{i} \mid c_{1}\right) \doteq Q\left(x_{i} \mid c_{1}, c_{3}^{\star}\right)=\pi\left(x_{i} \mid c_{1}, c_{3}^{\star}\right) \text { for } i \in\{1,2\}$ yields the same optimal reward.
Proposition 3에 의해, $C_3$는 $\{ X_1, X_2\}$에 대해 optimality하에서 쓸모없다.

예시3 $C_2$는 $C_1$과 $\mathbf X = \{ X_1, X_2\}$에 의해 막힌다

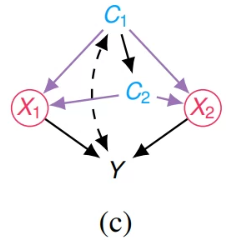
Joint distribution is factorized by $Q\left(c_{2} \mid c_{1}\right) \times \pi\left(x_{1} \mid c_{1}, c_{2}\right) \times \pi\left(x_{2} \mid c_{1}, c_{2}\right) \times P_{\mathbf{x}}\left(y, c_{1}\right)$
$\mu_{\boldsymbol{\pi}}=\sum_{c_{1}, c_{2}} Q\left(c_{2} \mid c_{1}\right)\left(\sum_{y, \mathbf{x}} y P_{\mathbf{x}}\left(y, c_{1}\right) \pi\left(x_{1} \mid c_{1}, c_{2}\right) \pi\left(x_{2} \mid c_{1}, c_{2}\right)\right) =: \sum_{c_{1}, c_{2}} Q\left(c_{2} \mid c_{1}\right) \mu_{\boldsymbol{\pi}}\left(c_{1}, c_{2}\right)$
- 정확하게 같진 않으나, $\mu_{\boldsymbol{\pi}}\left(c_{1}, c_{2}\right)$를 conditional reward라고 생각하면 편함
Let $c_{2}^{*}\left(c_{1}\right)=\arg \max _{c_{2}} \mu_{\boldsymbol{\pi}}\left(c_{1}, c_{2}\right)$
Then, $\mu_{\boldsymbol{\pi}} \leq \sum_{c_{1}} \mu_{\boldsymbol{\pi}}\left(c_{1}, c_{2}^{\star}\left(c_{1}\right)\right)=\sum_{y, c_{1}, \mathbf{x}} y P_{\mathbf{x}}\left(y, c_{1}\right) \pi\left(x_{1} \mid c_{1}, c_{2}^{\star}\left(c_{1}\right)\right) \pi\left(x_{2} \mid c_{1}, c_{2}^{\star}\left(c_{1}\right)\right)$
$\boldsymbol \pi$를 optimal policy w.r.t. $\mathcal S$라고 하면 등호 표현이 될 것이다.
Proposition 3에 의해, $C_2$는 $\{ X_1, X_2\}$에 대해 optimality하에서 쓸모없다.

예시4

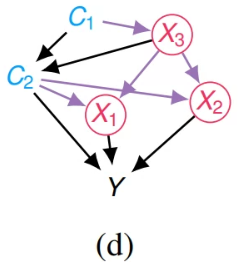
$\pi^{\prime}\left(x_{1} \mid c_{2}\right) \doteq \pi\left(x_{1} \mid x_{3}^{*}\left(c_{2}\right), c_{2}\right)$
Proposition 3에 의해, $X_3$는 $\{ X_1\}$에 대해 optimality하에서 쓸모없다.

MPS가 주어졌을 때, redundancy under optimality는 다양한 패턴으로 나타난다.

그런 redundancy를 찾는 grphical criterion을 제시한다.

Let $\mathbf{V}_{\prec V}$ denote a subset of $\mathbf{V}$ preceding $V \in \mathbf V$.

Lemma 1

Given an MPS $\mathcal S$, which satisfies non-redundancy (Thm 1),

let $\mathbf{X}^{\prime} \subseteq \mathbf{X}(\mathcal{S})$ be actions of interest and $\mathbf{C}^{\prime} \subsetneq \mathbf{C}_{\mathbf{X}^{\prime}} \backslash \mathbf{X}^{\prime}$ be non-action contexts of interest.

$^{\exists}$exogeneous variables $\mathbf U^{\prime}$ in $\mathcal G_{\mathcal S}$
$^\exists$subset of endogenous variables $\mathbf{Z} \supseteq \mathbf{C}_{\mathbf{X}^{\prime}} \backslash\left(\mathbf{C}^{\prime} \cup \mathbf{X}^{\prime}\right) \text { in } \mathcal{G}_{\mathcal{S}}$ that disjoints with $\mathbf{C}^{\prime} \dot \cup \mathbf{X}^{\prime}$
$^\exists$order $\prec$ over $\mathbf{V}^{\prime} \doteq \mathbf{C}^{\prime} \dot \cup \mathbf{X}^{\prime} \dot \cup \mathbf{Z}$

s.t.

$\begin{aligned} &\text{1. $\left(Y \perp \boldsymbol{\pi}_{\mathbf{X}^{\prime}} \mid\left\lceil\mathbf{X}^{\prime} \dot{\cup} \mathbf{C}^{\prime}\right\rceil\right)_{\mathcal{G}_{\mathcal{S}}}$} \\ &\text{2. $\left(C \perp \boldsymbol{\pi}_{\mathbf{X}_{\prec C}^{\prime}}, \mathbf{Z}_{\prec C}, \mathbf{U}^{\prime} \mid\left\lceil\left(\mathbf{X}^{\prime} \bigcup \mathbf{C}^{\prime}\right)_{\prec C}\right\rceil\right)_{\mathcal{G}_{\mathcal{S}}}$} \quad \text{for every $C \in \mathbf C^{\prime}$} \\ &\text{3. $\mathbf{V}_{\prec X}^{\prime}\supseteq p a(X)_{\mathcal{G}_{\mathcal{S}}} \quad $ for every $X \in \mathbf{X}^{\prime}$} \\ &\text{4. $\mathbf{V}_{\prec X}^{\prime} \cap\operatorname{de}(X)_{\mathcal{G}_{\mathcal{S}}} = \emptyset \quad $ for every $X \in \mathbf{X}^{\prime}$} \end{aligned}$

then, expected reward for deterministic and optimal w.r.t. $\mathcal S$ can be written as

$\mu_{\boldsymbol{\pi}}=\sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y, \mathbf{c}^{\prime}\right) \sum_{\mathbf{u}^{\prime}, \mathbf{z}} Q\left(\mathbf{u}^{\prime}\right) \prod_{Z \in \mathbf{Z}} Q\left(z \mid \mathbf{v}_{\prec z}^{\prime}, \mathbf{u}^{\prime}\right) \prod_{X \in \mathbf{X}^{\prime}} \pi\left(x \mid \mathbf{c}_{x}\right)$

(Proof)

$\begin{aligned} \mu_{\boldsymbol{\pi}} &=\sum_{y} y Q(y) \\ &=\sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q\left(y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}\right) \\ &=\sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q\left(y \mid \mathbf{c}^{\prime}, \mathbf{x}^{\prime}\right) Q\left(\mathbf{c}^{\prime}, \mathbf{x}^{\prime}\right) \\ &=\sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y \mid \mathbf{c}^{\prime}\right) Q\left(\mathbf{c}^{\prime}, \mathbf{x}^{\prime}\right) \quad \text{$\because$ Cond1} \\ &=\sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y \mid \mathbf{c}^{\prime}\right) \sum_{\mathbf{z}, \mathbf{u}^{\prime}} Q\left(\mathbf{c}^{\prime}, \mathbf{x}^{\prime}, \mathbf{z}, \mathbf{u}^{\prime}\right) \\ &=\sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y \mid \mathbf{c}^{\prime}\right) \sum_{\mathbf{z}, \mathbf{u}^{\prime}} \prod_{C \in \mathbf{C}^{\prime}} Q\left(c \mid \mathbf{v}_{\prec c}^{\prime}, \mathbf{u}^{\prime}\right) Q\left(\mathbf{u}^{\prime}\right) \prod_{V \in \mathbf{X}^{\prime} \cup \mathbf{Z}} Q\left(v \mid \mathbf{v}_{\prec v}^{\prime}, \mathbf{u}^{\prime}\right) \\ &=\sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y \mid \mathbf{c}^{\prime}\right) \prod_{C \in \mathbf{C}^{\prime}} Q^{\prime}\left(c \mid \mathbf{x}_{\prec c}^{\prime}, \mathbf{c}_{\prec c}^{\prime}\right) \sum_{\mathbf{z}, \mathbf{u}^{\prime}} Q\left(\mathbf{u}^{\prime}\right) \prod_{V \in \mathbf{X}^{\prime} \cup \mathbf{Z}} Q\left(v \mid \mathbf{v}_{\prec v^{\prime}}, \mathbf{u}^{\prime}\right) \quad \text{$\because$ Cond2 $C\perp \mathbf Z_{<C}, \mathbf U^{\prime} \mid \left(\mathbf{X}^{\prime} \bigcup \mathbf{C}^{\prime}\right)_{\prec C}$} \\ &=\sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y \mid \mathbf{c}^{\prime}\right) \prod_{C \in \mathbf{C}^{\prime}} Q_{\mathbf{x}^{\prime}_{ \prec c}}^{\prime}\left(c \mid \mathbf{c}_{\prec c}^{\prime}\right) \sum_{\mathbf{z}, \mathbf{u}^{\prime}} Q\left(\mathbf{u}^{\prime}\right) \prod_{V \in \mathbf{X}^{\prime} \cup \mathbf{Z}} Q\left(v \mid \mathbf{v}_{\prec v^{\prime}}, \mathbf{u}^{\prime}\right) \quad \text{$\because$ Cond2 $C\perp \boldsymbol \pi_{\mathbf X^\prime _{\prec C}} \mid \left(\mathbf{X}^{\prime} \bigcup \mathbf{C}^{\prime}\right)_{\prec C}$} \\ &=\sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y \mid \mathbf{c}^{\prime}\right) \prod_{C \in \mathbf{C}^{\prime}} Q_{\mathbf{x}^{\prime}}^{\prime}\left(c \mid \mathbf{c}_{\prec c}^{\prime}\right) \sum_{\mathbf{z}, \mathbf{u}^{\prime}} Q\left(\mathbf{u}^{\prime}\right) \prod_{V \in \mathbf{X}^{\prime} \cup \mathbf{Z}} Q\left(v \mid \mathbf{v}_{\prec v}^{\prime}, \mathbf{u}^{\prime}\right) \quad \because \text{Rule3} \\ &=\sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y \mid \mathbf{c}^{\prime}\right) Q_{\mathbf{x}^{\prime}}^{\prime}\left(\mathbf{c}^{\prime}\right) \sum_{\mathbf{z}, \mathbf{u}^{\prime}} Q\left(\mathbf{u}^{\prime}\right) \prod_{V \in \mathbf{X}^{\prime} \cup \mathbf{Z}} Q\left(v \mid \mathbf{v}_{\prec v}^{\prime}, \mathbf{u}^{\prime}\right) \\ &=\sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y, \mathbf{c}^{\prime}\right) \sum_{\mathbf{z}, \mathbf{u}^{\prime}} Q\left(\mathbf{u}^{\prime}\right) \prod_{Z \in \mathbf{Z}} Q\left(z \mid \mathbf{v}_{\prec z}^{\prime}, \mathbf{u}^{\prime}\right) \prod_{X \in \mathbf{X}^{\prime}} Q\left(x \mid \mathbf{v}_{\prec x}^{\prime}, \mathbf{u}^{\prime}\right) \\ &=\sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y, \mathbf{c}^{\prime}\right) \sum_{\mathbf{z}, \mathbf{u}^{\prime}} Q\left(\mathbf{u}^{\prime}\right) \prod_{Z \in \mathbf{Z}} Q\left(z \mid \mathbf{v}_{\prec z}^{\prime}, \mathbf{u}^{\prime}\right) \prod_{X \in \mathbf{X}^{\prime}} Q\left(x \mid \mathbf{c}_{x}\right) \quad \because \text{Cond3&4} \end{aligned}$

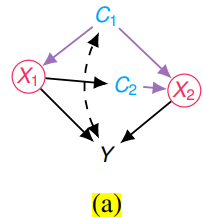
예시 (Lemma 1)

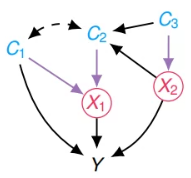
Let $\mathbf X^\prime = \left\{X_{1}, X_{2}\right\}$ be actions of interest.
Let $\mathbf{C}^{\prime}=\left\{C_{1}\right\}$
Consider $\mathbf{Z}=\left\{C_{2}, C_{3}\right\}$ and $\mathbf{U}^{\prime}=\emptyset$
Let $\prec=\left\langle C_{3}, C_{1}, X_{2}, C_{2}, X_{1}\right\rangle$ be the order over $\mathbf{V}^{\prime} = \mathbf{C}^{\prime} \dot \cup \mathbf{X}^{\prime} \dot \cup \mathbf{Z}$
$\mathbf X^\prime \dot\cup \mathbf C^\prime = \{ X_1, X_2, C_1\}$ and $\left\lceil\mathbf{X}^{\prime} \dot{\cup} \mathbf{C}^{\prime}\right\rceil = \{ X_1, X_2, C_1\}$
1 : $\text{$\left(Y \perp \boldsymbol{\pi}_{\mathbf{X}^{\prime}} \mid\left\lceil\mathbf{X}^{\prime} \dot{\cup} \mathbf{C}^{\prime}\right\rceil\right)_{\mathcal{G}_{\mathcal{S}}}$ } \Leftrightarrow \text{ $\left(Y \perp \{ C_1, C_2, C_3 \} \setminus \{ C_1\} \mid\{ X_1, X_2, C_1\}\right)_{\mathcal{G}_{\mathcal{S}}}$}$ is true.
2 : $\text{$\left(C_1 \perp \boldsymbol{\pi}_{\mathbf{X}_{\prec C_1}^{\prime}}\mid\left\lceil\left(\mathbf{X}^{\prime} \bigcup \mathbf{C}^{\prime}\right)_{\prec C_1}\right\rceil\right)_{\mathcal{G}_{\mathcal{S}}}$ $\Leftrightarrow$ $C_1 \perp \emptyset$}$ is true.
2 : $\text{$\left(C_1 \perp \mathbf{Z}_{\prec C_1}\mid\left\lceil\left(\mathbf{X}^{\prime} \bigcup \mathbf{C}^{\prime}\right)_{\prec C_1}\right\rceil\right)_{\mathcal{G}_{\mathcal{S}}}$ $\Leftrightarrow$ $C_1 \perp C_3$}$ is true.
3 : $\mathbf{V}_{\prec X_2}^{\prime}\supseteq p a(X_2)_{\mathcal{G}_{\mathcal{S}}}$ $\Leftrightarrow$ $\{ C_3, C_1\} \supseteq \{ C_3\}$ is true.
3 : $\mathbf{V}_{\prec X_1}^{\prime}\supseteq p a(X_1)_{\mathcal{G}_{\mathcal{S}}}$ $\Leftrightarrow$ $\{ C_3, C_1, X_2, C_2\} \supseteq \{ C_1, C_2\}$ is true.
4 : $\mathbf{V}_{\prec X_2}^{\prime}\cap de(X_2)_{\mathcal{G}_{\mathcal{S}}}$ $\Leftrightarrow$ $\{ C_3, C_1\} \cap \{ C_2, Y\} = \emptyset$ is true.
4 : $\mathbf{V}_{\prec X_1}^{\prime}\cap de(X_1)_{\mathcal{G}_{\mathcal{S}}}$ $\Leftrightarrow$ $\{ C_3, C_1, X_2, C_2\} \cap \{Y\} = \emptyset$ is true.
Hence,

$\begin{aligned} \mu_{\mathcal{S}}^{*} &=\sum_{y, \mathbf{x}, c_{1}} y Q_{\mathbf{x}}^{\prime}\left(y \mid c_{1}\right) \sum_{c_{23}} Q\left(c_{123}, \mathbf{x}\right) \\ &=\sum_{y, \mathbf{x}, c_{1}} y Q_{\mathbf{x}}^{\prime}\left(y \mid c_{1}\right) \sum_{c_{23}} Q\left(c_{3}\right) Q\left(c_{1} \mid c_{3}\right) Q\left(x_{2} \mid c_{13}\right) Q\left(c_{2} \mid c_{13}, x_{2}\right) Q\left(x_{1} \mid c_{123}, x_{2}\right) \\ &=\sum_{c_{3}} Q\left(c_{3}\right) \sum_{y, \mathbf{x}, c_{1}} y Q_{\mathbf{x}}^{\prime}\left(y, c_{1}\right) \sum_{c_{2}} Q\left(c_{2} \mid c_{13}, x_{2}\right) \pi\left(x_{2} \mid c_{3}\right) \pi\left(x_{1} \mid c_{12}\right) \end{aligned}$

추가로, $C_2$와 $C_3$가 redundant context under optimality라는 것을 보이겠다.

Theorem 2

Let $\mathbf U^\prime, \, \mathbf Z,$ and $\prec$ satisfy Lemma 1.

For $Z \in \mathbf Z$, let $\mathbf V_Z$ be a minimal subset of $\mathbf{V}_{\prec Z}^{\prime} \cup \mathbf{U}^{\prime}$ s.t. $Q\left(Z \mid \mathbf{V}_{Z}\right)=Q\left(Z \mid \mathbf{V}_{\prec Z}^{\prime}, \mathbf{U}^{\prime}\right)$.

Let $\text {fix}(\mathbf{T})$ w.r.t. $\left\{\left\langle Z, \mathbf{V}_{Z}\right\rangle\right\}_{Z \in \mathbf{Z}}$ be $\hat{\mathbf{T}} \doteq\lceil\mathbf{T}\rceil \cup\left\{Z \in \mathbf{Z} \mid \mathbf{V}_{Z} \backslash \mathbf{U}^{\prime} \subseteq\lceil\mathbf{T}\rceil\right\}$

Let $\text {fixed}(\mathbf{T}) = \left\{\begin{array}{l} \mathbf T \quad &\text{if } \mathbf{T}=\hat{\mathbf{T}} \\ \text {fixed}(\mathbf {\hat T}) \quad &\text{o.w.} \end{array}\right.$

$\mathbf T$에서 시작해서 ($\mathbf U^\prime$이 고정일 때) 이들로 결정되는 $X$와 $Z$가 연쇄적으로 추가된다.

If $\operatorname{fixed}\left(\mathbf{C}_{X} \setminus\mathbf{Z}\right) \supseteq \mathbf{C}_{X}$ for every $X \in \mathbf{X}^{\prime}$, then

$\mathcal{S}^{\prime} \doteq\left(\mathcal{S} \setminus \mathbf{X}^{\prime}\right) \cup\left\{\left\langle X, \mathbf{C}_{X} \setminus \mathbf{Z}\right\rangle\right\}_{X \in \mathbf{X}^{\prime}} \text { satisfies } \mu_{\mathcal{S}^{\prime}}^{*}=\mu_{\mathcal{S}}^{*}$

모든 $X$에 대해, $\mathbf{C}_{X} \setminus\mathbf{Z}$로 결정되는 애들이 $\mathbf C_{X}$를 포함한다면, $\mathbf Z$는 필요없음

(Proof)

$\begin{aligned} \mu_{\boldsymbol{\pi}} =&\sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y, \mathbf{c}^{\prime}\right) \sum_{\mathbf{z}, \mathbf{u}^{\prime}} Q\left(\mathbf{u}^{\prime}\right) \prod_{Z \in \mathbf{Z}} Q\left(z \mid \mathbf{v}_{\prec z}^{\prime}, \mathbf{u}^{\prime}\right) \prod_{X \in \mathbf{X}^{\prime}} Q\left(x \mid \mathbf{c}_{x}\right) \quad \because \text{Lemma 1} \\ =&\sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y, \mathbf{c}^{\prime}\right) \sum_{\mathbf{z}, \mathbf{u}^{\prime}} Q\left(\mathbf{u}^{\prime}\right) \prod_{Z \in \mathbf{Z}} Q\left(z \mid \mathbf{v}_{z}\right) \prod_{X \in \mathbf{X}^{\prime}} Q\left(x \mid \mathbf{c}_{x} \backslash \mathbf{z}, \mathbf{c}_{x} \cap \mathbf{z}\right) \\ =&\sum_{\mathbf{u}^{\prime}} Q\left(\mathbf{u}^{\prime}\right)\Bigg(\sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y, \mathbf{c}^{\prime}\right) \sum_{\mathbf{z}} \prod_{Z \in \mathbf{Z}} Q\left(z \mid \mathbf{v}_{z}\right) \prod_{X \in \mathbf{X}^{\prime}} Q\left(x \mid \mathbf{c}_{x} \backslash \mathbf{z}, \mathbf{c}_{x} \cap \mathbf{z}\right)\Bigg) \\ \leq& \sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y, \mathbf{c}^{\prime}\right) \sum_{\mathbf{z}} \prod_{Z \in \mathbf{Z}} Q\left(z \mid \mathbf{v}_{z} \backslash \mathbf{U}^{\prime},\left(\mathbf{V}_{Z} \cap \mathbf{u}^{\prime *}\right)\right) \prod_{X \in \mathbf{X}^{\prime}} Q\left(x \mid \mathbf{c}_{x} \backslash \mathbf{z}, \mathbf{c}_{x} \cap \mathbf{z}\right) \\ \\ & \quad \text{where $\mathbf{u}^{\prime *} = \arg\max_{\mathbf u ^{\prime}}\Big( \cdots\Big)$} \\ =&\sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y, \mathbf{c}^{\prime}\right) \sum_{z_{1}} Q\left(z_{1} \mid \mathbf{v}_{z_{1}} \backslash \mathbf{U}^{\prime},\left(\mathbf{V}_{Z_{1}} \cap \mathbf{u}^{\prime *}\right)\right) \\ & \Bigg ( \sum_{\mathbf{z} \backslash\left\{z_{1}\right\}} \prod_{Z \in \mathbf{Z} \backslash\left\{Z_{1}\right\}}Q\left(z \mid \mathbf{v}_{z} \backslash \mathbf{U}^{\prime},\left(\mathbf{V}_{Z} \cap \mathbf{u}^{\prime *}\right)\right) \prod_{X \in \mathbf{X}^{\prime}} Q\left(x \mid \mathbf{c}_{x} \backslash \mathbf{z}, \mathbf{c}_{x} \cap \mathbf{z}\right) \Bigg) \\ \\ & \quad \text{where $Z_1$ is the first $\mathbf Z$ in $\prec$} \\ \leq& \sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y, \mathbf{c}^{\prime}\right) \times \\ & \quad\sum_{\mathbf{z} \backslash\left\{z_{1}\right\}} \prod_{Z \in \mathbf{Z} \backslash\left\{Z_{1}\right\}} Q\Big(z \mid \mathbf{v}_{z} \backslash\left(\mathbf{U}^{\prime} \cup\left\{Z_{1}\right\}\right),\left(\mathbf{V}_{Z} \cap\left\{\mathbf{u}^{\prime *}, z_{1}^{*}\left(\mathbf{v}_{z_{1}} \backslash \mathbf{U}^{\prime}, \mathbf{v}_{z_{1}} \cap \mathbf{u}^{\prime *}\right)\right\}\right)\Big) \\ &\qquad \qquad \prod_{X \in \mathbf{X}^{\prime}} Q\left(x \mid \mathbf{c}_{x} \backslash \mathbf{Z}, \mathbf{c}_{x} \cap\left(\mathbf{z} \backslash\left\{Z_{1}\right\}, z_{1}^{*}\left(\mathbf{v}_{z_{1}} \backslash \mathbf{U}^{\prime}, \mathbf{v}_{z_{1}} \cap \mathbf{u}^{\prime *}\right)\right)\right) \\ \\ & \quad \text{where $z_{1}^{*}(\cdot)=z_{1}^{*}\left(\mathbf{v}_{z_{1}} \backslash \mathbf{U}^{\prime}, \mathbf{v}_{z_{1}} \cap \mathbf{u}^{\prime *}\right)$ is for some ftn of free variables$\mathbf V_{Z_1} \setminus \mathbf U^\prime \mapsto \mathbb R$} \\ \\ \leq& \cdots \\ \leq& \sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y, \mathbf{c}^{\prime}\right) \prod_{X \in \mathbf{X}^{\prime}} Q\left(x \mid \mathbf{c}_{x} \backslash \mathbf{Z}, \mathbf{c}_{x} \cap\left\{z_{i}^{*}(\cdot)\right\}_{i=1}^{m}\right) \\ \\ & \quad \text{where $z_{i}^{\star}(\cdot)= z_{i}^{\star}\left(\mathbf{v}_{z_{i}} \backslash\left(\mathbf{U}^{\prime} \cup \mathbf{Z}_{<i}\right), \mathbf{v}_{z_{i}} \cap\left(\mathbf{u}^{\prime \star} \cup\left\{z_{j}^{\star}(\cdot)\right\}_{j=1}^{i-1}\right)\right)$} \end{aligned}$

unobserved variable이 $\mathbf{u}^{\mathbf{\prime} \star}$로 고정된 상황에서, $\mathbf{c}_{x} \backslash \mathbf{Z}$의 값이 $\mathbf{c}_{x} \cap\left\{z_{i}^{\star}(\cdot)\right\}_{i=1}^{m}$들을 결정한다면,

$\pi^{\prime}(x \mid \mathbf{c}_{x} \backslash \mathbf{Z}) = Q\left(x\left|\mathbf{c}_{x}\right| \mathbf{Z}, \mathbf{c}_{x} \cap\left(\mathbf{z} \backslash\left\{Z_{1}\right\}, z_{1}^{*}\left(\mathbf{v}_{z_{1}} \mid \mathbf{U}^{\prime}, \mathbf{v}_{z_{1}} \cap \mathbf{u}^{\prime *}\right)\right)\right)$

인 policy $\boldsymbol \pi^\prime$이 존재한다.

$\mu_{\boldsymbol{\pi}} \leq \sum_{y, \mathbf{c}^{\prime}, \mathbf{x}^{\prime}} y Q_{\mathbf{x}^{\prime}}^{\prime}\left(y, \mathbf{c}^{\prime}\right) \prod_{X \in \mathbf{X}^{\prime}} \pi^{\prime}\left(x \mid \mathbf{c}_{x} \backslash \mathbf{Z}\right)$

Theorem 2는 Lemma 1의 표현식이 $\mu^*_{\mathcal S^\prime}$으로 바뀔 수 있는 조건을 제공한다.

$Q\left(z \mid \mathbf{v}_{\prec z}^{\prime}, \mathbf{u}^{\prime}\right) \Rightarrow Q(z \mid \mathbf v_z)$ for every $Z \in \mathbf Z$
$\pi(x \mid \mathbf c_x ) \Rightarrow \pi^\prime (x \mid \mathbf c_x \setminus \mathbf z)$ for every $X\in \mathbf X^\prime$

예시 (Lemma 1 + Theorem 2)

$\begin{aligned} \mu_{\mathcal{S}}^{*} &=\sum_{c_{3}} Q\left(c_{3}\right) \sum_{y, \mathbf{x}, c_{1}} y Q_{\mathbf{x}}^{\prime}\left(y, c_{1}\right) \sum_{c_{2}} Q\left(c_{2} \mid c_{13}, x_{2}\right) \pi\left(x_{2} \mid c_{3}\right) \pi\left(x_{1} \mid c_{12}\right) \\ &\leq \sum_{y, \mathbf{x}, c_{1}} y Q_{\mathbf{x}}^{\prime}\left(y, c_{1}\right) \sum_{c_{2}} Q\left(c_{2} \mid c_{1}, c_{3}^{*}, x_{2}\right) \pi\left(x_{2} \mid c_{3}^{*}\right) \pi\left(x_{1} \mid c_{1}, c_{2}\right) \\ &\leq \sum_{y, \mathbf{x}, c_{1}} y Q_{\mathbf{x}}^{\prime}\left(y, c_{1}\right) \sum_{c_{2}} Q\left(c_{2} \mid c_{1}, c_{3}^{*}, x_{2}^{*}\right) \pi^{\prime}\left(x_{2}\right) \pi\left(x_{1} \mid c_{1}, c_{2}\right) \quad \text{where $\pi^\prime(x_2) = \mathbf I_{x^*_2}(x_2)$} \\ & =\sum_{c_{1}, c_{2}} Q\left(c_{2} \mid c_{1}, c_{3}^{*}, x_{2}^{*}\right) \sum_{y, \mathbf{x}} y Q_{\mathbf{x}}^{\prime}\left(y, c_{1}\right) \pi^{\prime}\left(x_{2}\right) \pi\left(x_{1} \mid c_{1}, c_{2}\right) \\ \\ \because &\operatorname{fixed}(C_{X_2} \setminus \mathbf Z) =\operatorname{fixed}(\emptyset) =\left\{C_{3}, X_{2}\right\} \supseteq \mathbf C_{X_2} = \{ C_3\} \\ \\ & \leq \sum_{y, \mathbf{x}, c_{1}} y Q_{\mathbf{x}}^{\prime}\left(y, c_{1}\right) \pi^{\prime}\left(x_{2}\right) \pi\left(x_{1} \mid c_{1}, c_{2}^{*}\left(c_{1}\right)\right) \\ &=\sum_{y, \mathbf{x}, c_{1}} y Q_{\mathbf{x}}^{\prime}\left(y, c_{1}\right) \pi^{\prime}\left(x_{1} \mid c_{1}\right) \pi^{\prime}\left(x_{2}\right)=\mu_{\mathcal{S}^{\prime}}^{*} \\ \\ \because &\operatorname{fixed}(C_{X_1} \setminus \mathbf Z) =\operatorname{fixed}\left(\left\{C_{1}\right\}\right)=\left\{C_{1}, C_{3}, X_{2}, C_{2}\right\} \supseteq \mathbf C_{X_1} = \left\{C_{1}, C_{2}\right\} \\ &\text{Note that $\mathbf V_{C_2} = \{ C_1, C_3, X_2\}$} \end{aligned}$

Hence, $\mathcal S$ is not NRO due to $\{ C_2, C_3\}$ is redundant to $\{ X_1, X_2\}$

4. A Partial Order over Mixed Policies and Possible-Optimality

NRO에 기반해, agent는 MPS를 더 효율적으로 최적화할 수 있다.

그러나, 어떤 NRO MPS가 최적화할만 한 지에 대한 질문이 남아있다.

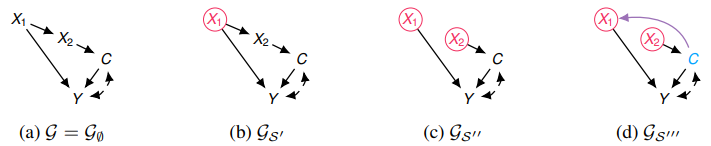
이들은 모두 NRO MPS들이다.

Environment와의 상호작용 없이, $\mu \leq \mu_{\mathcal{S}^{\prime}}^{\star} \leq \mu_{\mathcal{S}^{\prime \prime}}^{\star} \leq \mu_{\mathcal{S}^{\prime \prime \prime}}^{*}$임을 보일 수 있다.

$\mu \leq \mu_{\mathcal{S}^{\prim\star}}^{\star}
- $f(x_1):= \mathbb E\left[Y \mid X_1 = x_1\right] = \mathbb E\left[Y \mid \hat X_1 = x_1\right]$
- $x_1^* := f(x_1)$
$\mu_{\mathcal{S}^{\prime}}^{\star} \leq \mu^\star_{\mathcal{S}^{\prime \prime}}^{\star}$
- $f_{x_1^\star}(x_2):= \mathbb E \left[ Y \mid \hat X_1 = x_1^\star, X_2 = x_2\right]= \mathbb E \left[ Y \mid \hat X_1 = x_1^*, \hat X_2 = x_2\right]$
- $x_2^\star := \arg\max _{x_2} f_{x_1^\star}(x_2)$
$\mu_{\mathcal{S}^{\prime \prime}}^{\star} \leq \mu_{\mathcal{S}^{\prime \prime \prime}}^{\star}$
- CU에 대한 정보를 반영하여 $X_1$을 결정하기 때문에

Definition 5 (Possibly-Optimal MPS)

Given $\left\langle\mathcal{G}, \mathbf{X}^{\star}, \mathbf{C}^{\star}, Y\right\rangle$, let $\mathbb S$ be a set of NRO MPSes.

An MPS $\mathcal S \in \mathbb S$ is said to be possibly-optimal if $^\exists \mathcal M \sim \mathcal G$ s.t. $\mu_{\mathcal{S}}^{\star}>\max _{\mathcal{S}^{\prime} \in \mathbb{S} \setminus\{\mathcal{S}\}} \mu_{\mathcal{S}^{\prime}}^{\star}$

Partial order sense에서, POMPS는 $\mathbb S$에서 최상단의 원소들이다.

Partial order를 보기 전에, MPS를 취해서 improved MPS를 뱉는 operator를 소개하겠다.

adding observations for existing actions
adding new intervention

이들은 non-POMPS들을 찾는데 sufficient condition을 제공한다.

Proposition 4

Given an MPS $\mathcal S$ and $X \in \mathbf X (\mathcal S)$, adding $C \in \mathbf C^\star$ as a context of $X$, i.e.

$\mathcal{S}^{\prime}=(\mathcal{S} \setminus \{X\}) \cup\left\{\left\langle X, \mathbf{C}_{X} \cup\{C\}\right\rangle\right\}$ improves $\mathcal S$ if

$C \not \in de(X)_{G_\mathcal S}$ and
$C \perp Y \mid\left\lceil\mathbf{C}_{X}\right\rceil \text { in } \mathcal{H} \backslash\{X\}$

$\not \perp$ 아닌가? 아예 isolated된 node도 이 조건을 만족함.

4.1 Adding new interventions

Intervention은 $X \in \mathbf X^*$의 mechanism을 인공적인 $\pi (x \mid \mathbf z)$로 바꾼다.

Intervention이 더 나음을 보장하려면, 기존의 $X$가 어떤 정보를 취했고 새로운 context를 어떤 정보를 지니는 지를 고려해야한다.

만약 모든 $X$의 부모가 context로 사용될 수 있다면(UC가 없다면), trivial하다.

UC가 있다면 backdoor path의 존재를 조사해야한다.

Let $Q= P_{\boldsymbol \pi}$ and $\mathcal H = \mathcal G_{\boldsymbol \pi}$ for some $\mathcal S \sim ^{-1}\boldsymbol \pi$

$\mathcal S \sim ^{-1}\boldsymbol \pi$이 뭔 지 모르겠지만

Given $X \in \mathbf X^{\star} \setminus \mathbf X(\boldsymbol \pi)$ and $\mathbf Z \subseteq \mathbf C^\star \setminus \{ X\}$,

if $\left\{\begin{array}{l}
\text { (i) Rule 2 : }(Y \perp X \mid\lceil\mathbf{Z}\rceil)_{\mathcal{H}_{\underline{X}}}\\ \text{and }\\
\text { (ii) Rule 3 : } X \notin \operatorname{an}(\mathbf{Z})_{\mathcal{H}}
\end{array}\right.$ then,

$\begin{aligned} \mu_{\boldsymbol{\pi}} &=\sum_{y, x, \mathbf{z}} y Q(y \mid x, \mathbf{z}) Q(x \mid \mathbf{z}) Q(\mathbf{z}) \\ &\stackrel{(\mathrm{i})}{=} \sum_{y, x, \mathbf{z}} y Q_{x}^{\prime}(y \mid \mathbf{z}) Q(x \mid \mathbf{z}) Q(\mathbf{z}) \\ &\stackrel{\text { (ii) }}{=} \sum_{y, x, \mathbf{z}} y Q_{x}^{\prime}(y \mid \mathbf{z}) Q(x \mid \mathbf{z}) Q_{x}^{\prime}(\mathbf{z}) \\ &\doteq \sum_{y, x, \mathbf{z}} y Q_{x}^{\prime}(y, \mathbf{z}) \pi^{\prime}(x \mid \mathbf{z}) \doteq \mu_{\boldsymbol{\pi}^{\prime}} \end{aligned}$

$\boldsymbol \pi^\prime$은 최적화될 여지가 남아있으므로 $\mu_{\mathcal{S}}^{\star} \leq \mu_{\mathcal{S} \cup\{\langle X, \mathbf{Z}\rangle\}}^{*}$이다.

하지만, 위의 기준을 set of interventions으로 확장하기엔 문제가 있다.

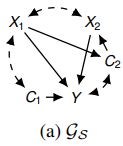
$\{ X_1, X_2\}$, $\mathbf Z = \{C_2 \}$일 때, 모든 condition이 깨지기 때문이다.

Intervention을 동시에 추가하기 위해선…

Theorem 3

Given an MPS $\mathcal S$, let $\mathcal S^\prime \neq \mathcal S$ be an MPS with $\mathbf{X}(\mathcal{S}) \subseteq \mathbf{X}\left(\mathcal{S}^{\prime}\right)$ s.t. $\mathcal H ^{\prime \prime} = \mathcal{G}_{\mathcal{S}} \cup \mathcal{G}_{\mathcal{S}^{\prime}}$ is acyclic.

Let $X^\prime = \left(\mathbf{X}\left(\mathcal{S}^{\prime}\right) \backslash \mathbf{X}(\mathcal{S})\right) \cup\left\{X \in \mathbf{X}(\mathcal{S}) \mid \mathbf{C}_{x}^{\prime} \neq \mathbf{C}_{X}\right\}$; (기존 MPS와 다른 action들)

Let $\mathcal{S}^{\prime \prime} \doteq\left\{\left\langle X, p a(X)_{\mathcal{H}^{\prime \prime}} \cup \mathbf{U}_{X}\right\rangle\right\}_{X \in \mathbf{X}^{\prime}}$ (intermediate MPS)

If $\mu_{\mathcal{S}^{\prime \prime}}^{\star}=\mu_{\mathcal{S}}^{\star}$ can be elicited by Thm2, then $\mu_{\mathcal{S}}^{\star} \leq \mu_{\mathcal{S}^{\prime}}^{\star}$

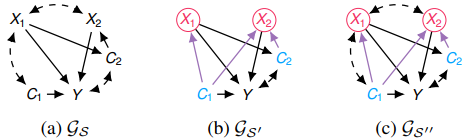
$\mathrm{U}^{\prime}=\emptyset \text { and } \prec=\left\langle C_{1}, \mathbf{U}_{X_{1}}, \mathbf{U}_{X_{2}}, X_{1}, C_{2}, X_{2}\right\rangle$ 로 두고 Theorem 2를 적용하면 $\mu_{\mathcal{S}}^{\star} \leq \mu_{\mathcal{S}^{\prime \prime}}^{\star}$를 확인할 수 있다.

$\mu_{\mathcal{S}}^{\star} \leq \mu_{\mathcal{S}^{\prime \prime}}^{\star}$ 는 자명하므로, $\mu_{\mathcal{S}}^{\star} \leq \mu_{\mathcal{S}^{\prime}}^{\star}$ 임을 알 수 있고 $\mathcal S$는 POMPS가 아니다.

4.2 Refining the space of MPSes

Brute Force : Thm2 + Thm3 + Prop4

Study Repo

Characterizing Optimal Mixed Policies