Transportability of Causal and Statistical Relations: A Formal Approach

0. Abstract

특정 환경에서의 experiment로 학습된 결과를 다른 환경으로 transfer하는 문제를 다룬다.

Target domain에서의 effect가 source domain에서의 실험들로 추론될 수 있는 지를 결정하는 procedure를 유도한다.

Observational transportability에 대해서도 다룬다.

1. Introduction

과학은 실험실에서 얻어진 결론들을 다른 환경으로 generalize한다.

만약 target environment가 너무 다르다면, 아무 것도 일반화되지 않는다.

그러나 대부분의 실험은 apply에 목적을 두고 실행됐기에, 이러한 generalization이 정당화할만큼 유사한 environment를 채택한다.

놀랍게도 transport를 허용하는 condition은 체계적으로 다뤄진 적이 없다.

이 주제에 괜해서, meta analysis 등 구두로 서술하는 것들이 있다.

반면에 이 논문은 formal condition을 세운다.

---

ML literature에서 training과 test의 환경의 차이에 대해 걱정하면서도, prediction 성능에만 집중하고 있다.

사전의 causal knowledge를 learning process에 담고있지 않기 때문에 차이에 대한 이론적 보장들은 없다.

이 논문은 연구자들에게 domain-specific knowledge가 사용 가능할 때, 아래의 것들을 알려준다.

• 무엇이 얻어질 수 있는 지
• 왜 transfer learning이 실패하는 지

2. Motivating Examples

우리의 discussion을 motivate하기 위해 3가지의 간단한 예시를 보이겠다.

이들은 임상실험을 떠올리게 하나 data-generating model으로 characterize되는 모든 learning environment와 관련있다.

예를 들어, simulator로 학습된 로봇은 학습에서 얻어진 causal knowledge를 비싼 실제 환경으로 transport할 수 있어야 한다.

---

Example 1

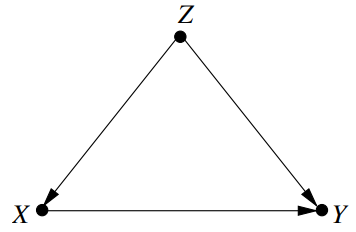
LA에서 randomized experiment를 하여서 age($Z$) 그룹별로 CE of $X$ on $Y$를 쟀다.

그 결과를 NYC로 일반화하고자 한다.

그러나 우리는 $P(x, y, z)$와 $P^*(x, y, z)$가 다름을 알고있다.

어떻게 $P^{*}(y \mid d o(x))$를 estimate 할 수 있을까?

만약 $Z$-specific effect $P(y \mid do(x) , z)$ 가 invariant하다면,

$$P^{*}(y \mid d o(x))=\sum P(y \mid d o(x), z) P^{*}(z)$$

로 구해질 수 있다.

---

Example 2 (proxy variable)

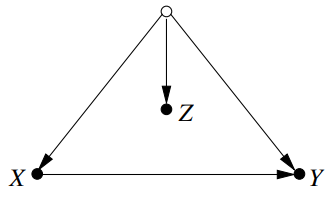
Example 1 상황에서, $Z$를 age와 상관관계가 있는 언어구사수준이라고 해보자.

LA에서의 $Z$-specific effect $P(y \mid do(x) , z)$로 부터 $P^{*}(y \mid d o(x))$를 estimate 할 수 있을까?

만약 두 도시의 age의 marginal distribution이 같다면, $Z$의 분포랑 상관 없이 $P^{*}(y \mid d o(x))=P(y \mid d o(x))$ 이다.

반면에, $P(z \mid a g e)$의 invariance를 가정한 상황에서 $P(z) \neq P^{*}(z)$의 다름은 age의 marginal distribution의 다름을 의미한다.

이 상황에서 transportability는 causal context에 의존하게 된다.

---

Note that

• Example 1에선 $Z$-specific effect가 invariant 하다.
• Example 2에선 $Z$-specific effect가 invariant 하지 않다.
  • $P^{}(y \mid d o(x), z)=\sum_{a g e} P(y \mid d o(x), \text { age }) P^{}(\operatorname{age} \mid z)$
  • $P(y \mid d o(x), z)=\sum_{a g e} P(y \mid d o(x), \text { age }) P(\operatorname{age} \mid z)$

---

Example 3 ($X$-dependent variable)

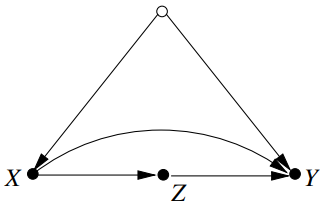
$Z$를 관측되는 질병의 수치라고 생각해보자.

추가로 $P(z) \neq P^{*}(z)$를 가정하자.

$P(y \mid do(x), z)$가 LA에서 estimate이 됐다고 가정하자.

이 경우에 $P^*(y \mid do(x))$를 잴 수 있을까?

$$\begin{aligned} P^{*}(y \mid d o(x))&=\sum_{z} P^{*}(y \mid d o(x), z) P^{*}(z \mid d o(x)) \\ &= \sum_{z} P(y \mid d o(x), z) P^{*}(z \mid x) \quad \because \text{Rule 3} \end{aligned}$$

3. Formalizing Transportability

3.1 Selection Diagram and Selection Variables

위의 예시들은 transportability가 causal thing이라는 것을 설명한다.

$P$가 같든 말든 structure에 기반해서 다른 transport formula가 나오므로

도메인의 다름을 formal하게 나타내기 위해 causal diagram with selection variables를 사용한다.

---

Population $\Pi^*$에서 experimental study를 했었다면 얻어졌을 interventional distribution을 selection variable로 표기한다.

$$P^{*}(v \mid d o(x))=P\left(v \mid d o(x), s^{*}\right)$$

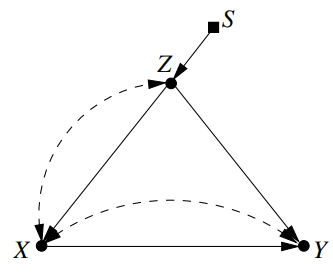
• $Y$를 가르키는 $S$ 변수의 부재는 age-specific effects가 invariant 함을 암시한다.
• $P(z) \neq P^*(z)$는 $P(z) \neq P(z \mid s)$로 나타낸다.

• Structural difference를 나타내는 데도 쓸 수 있다.
• Mechanism의 invariance에 대한 믿음이 없을 때 모든 변수에 selection variable을 붙일 수 있다.

3.2 Transportability: Definitions and Examples

Selection diagram + do-calculus + identifiability => transportability의 formal definition 제공

---

Definition 1 (Transportability)

​ Given two domains $\Pi$ and $\Pi^$, characterized by $(P, G)$ and $(P^, G^*)$,

​ a causal relation $R$ is said to be transportable $\Pi \Rightarrow \Pi^*$ if

• $R(\Pi)$ is estimable from $\Pi+I$
• and
• $R(\Pi^)$ is identified from $(\Pi+I) + \Pi^$

---

위의 정의는 $R(\Pi^*)$의 identifiability(랑 비슷한 느낌)을 요구한다.

이는 모델이 클 수록 확인하기 어렵다.

그러므로 우리는 transportability에 대한 procedural criteria를 찾게된다.

이는 단계적으로 쪼개서 transportability를 결정하는 것이다.

---

Theorem 1

​ Let $D$ be the selection diagram characterizing $\Pi$ and $\Pi^*$

​ Let $S$ be a set of selection variables in $D$

​ The relation $R=P(y \mid d o(x), z)$ is transportable from $\Pi\Rightarrow \Pi^*$

​ iff

​ $P(y \mid d o(x), z, s)$ is reducible to an expression in which $S$ only appears at $do$-free terms.

(Proof)

<==

​ $do$-free term은 $\Pi^*$로 estimate이 가능하므로

==>

​ If $R$ is transportable, $R(\Pi^)$ is identifiable from $(\Pi+I) + \Pi^$

​ $do-$calculus의 completeness

---

Definition 2 (Direct Transportability)

​ A causal relation $R$ is said to be directly transportable $\Pi ==> \Pi^$ if $R\left(\Pi^{}\right)=R(\Pi)$

---

$R = P(y\mid do(x))$의 direct transportability는 $(S \perp Y \mid X)_{G \bar{X}}$ 로 확인될 수 있다.

$$R\left(\Pi^{*}\right)=P(y \mid d o(x), s)=P(y \mid d o(x))=R(\Pi)$$

---

Example 4

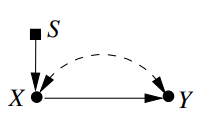
$X=x$ 로 intervention을 할 경우, $S$는 $Y$에 아무런 영향을 미치지 않는다.

---

Definition 3 (Trivial Transportability)

​ A causal relation $R$ is said to be trivially transportable $\Pi \Rightarrow \Pi^$ if $R\left(\Pi^{}\right)$ is identifiable from $\Pi^*$

4. Transportability of Causal Effects: A Graphical Criterion

Selection diagram이 주어졌을 때, $R$의 transportability와 transport formula를 제공하는 정리들을 증명하겠다.

---

Theorem 2

​ Let $D$ be the selection diagram characterizing $\Pi$ and $\Pi^*$.

​ Let $S$ be the selection variables in $D$

​ The $Z$-specific causal effect $P(y \mid do(x), z)$ is transportable $\Pi \Rightarrow \Pi^*$ if $(Y \perp S \mid Z)_{D_{\bar{X}}}$

---

Definition 4 (S-admissibility)

​ A set of variables $Z$ is called $S$-admissible if $(Y \perp S \mid Z)_{D_{\bar X}}$

---

Corollary 1

​ The average causal effect $P(y \mid do(x))$ is transportable $\Pi \Rightarrow \Pi^*$ if $^\exists$pre-treatment $Z$ satisfies $S$-admissible.

​ Moreover, the transport formula is given by

$$P^{*}(y \mid d o(x))=\sum_{z} P(y \mid d o(x), z) P^{*}(z)$$

---

Example 7

• $Z$ is $S$-admissible

• empty set is $S$-admissible

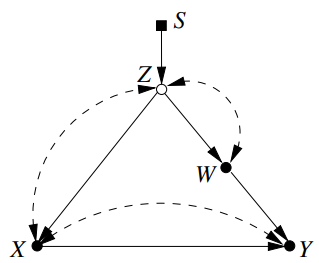
• $W$ is $S$-admissible

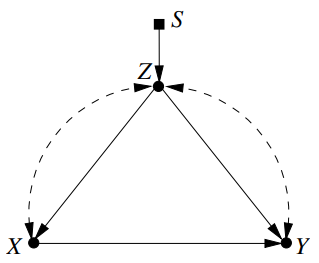
• $^{\not \exists} S$-admissible set

---

Corollary 2

​ Any $S$ that can be ignored

• is pointing directly into $X$
• or
• is d-connected only through $X$

---

이는 컨셉적으로, treatment를 결정하는 성향의 차이가 randomization으로 해결될 수 있음을 의미한다.

---

Theorem 3

​ The causal effect $P(y \mid do(x))$ is transportable $\Pi \Rightarrow \Pi^*$ if any one of conditions holds

1. $P(y \mid do(x))$ is trivially transportable
2. $^{\exists} Z$ s.t. $Z$ is $S$-admissible and $P(z \mid do(x))$ is transportable.
3. $^{\exists} W$ s.t. $(X \perp Y \mid W, S) _D$ and $P(w \mid do(x))$ is transportable.

(Proof)

1. trivially transportable implies transportable
2. $$\begin{aligned} P^{*}(y \mid d o(x)) &=P(y \mid d o(x), s) \\ &=\sum_{z} P(y \mid d o(x), z, s) P(z \mid d o(x), s) \\ &=\sum_{z} P(y \mid d o(x), z) P^{*}(z \mid d o(x)) \end{aligned}$$
3. $$\begin{aligned} P^{*}(y \mid d o(x)) &=P(y \mid d o(x), s) \\ &=\sum_{w} P(y \mid d o(x), w, s) P(w \mid d o(x), s)\\ &=\sum_{w} P(y \mid w, s) P^{*}(w \mid d o(x)) \quad \because\text{Rule 3}\\ &=\sum_{w} P^{*}(y \mid w) P^{*}(w \mid d o(x))\end{aligned}$$

---

Remark

• Theorem3에서 2와 3의 condition은 recursive이다.
• 피드백이 없는 system에선 유한한 단계를 거쳐서 끝난다.
• 하지만 not complete이다…(?)

---

Example 8

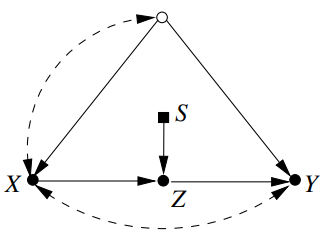
• front-door criterion : $R = P(y \mid do(x))$는 trivially transportable이다.

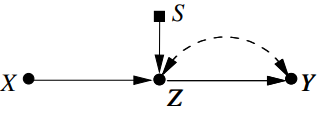
• $Z$는 $S$-admissible set이다.
• $P(z \mid do(x))$는 (trivially) transportable이다.

• $S$-admissible set이 없다.
• $(X \perp Y \mid W, S) _D$를 만족하는 $W$도 없다.

---

Example 9

$$\begin{aligned} P^{*}(y \mid d o(x))&=P(y \mid d o(x), s) \\ &=\sum_{z} P(y \mid d o(x), s, z) P(z \mid d o(x), s) \\ &=\sum_{z} P(y \mid d o(x), z) P(z \mid d o(x), s) \quad \because\text{$Z$'s $S$-admissibility for CE of X on Y}\\ &=\sum_{z} P(y \mid d o(x), z) \sum_{w} P(z \mid d o(x), w, s) P(w \mid d o(x), s)\\ &=\sum_{z} P(y \mid d o(x), z) \sum_{w} P(z \mid w, s) P(w \mid d o(x), s) \quad \because (X \perp Z \mid S, W)_{D}\\ &=\sum_{z} P(y \mid d o(x), z) \sum_{w} P^{*}(z \mid w) P(w \mid d o(x)) \quad \because\text{$\{ \}$'s $S$-admissibility for CE of X on Y} \end{aligned}$$

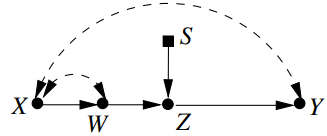
Example 10

$$\begin{aligned} P^{*}(y \mid d o(x))&=P\left(y \mid d o(x), s, s^{\prime}\right)\\ &=\sum_{z} P\left(y \mid d o(x), s, s^{\prime}, z\right) P\left(z \mid d o(x), s, s^{\prime}\right)\\ &=\sum_{z} P(y \mid d o(x), z) P\left(z \mid d o(x), s, s^{\prime}\right) \quad \because\text{$Z$'s $S$-admissibility for CE of X on Y}\\ &=\sum_{z} P(y \mid d o(x), z) \sum_{w} P\left(z \mid d o(x), s, s^{\prime}, w\right) P\left(w \mid d o(x), s, s^{\prime}\right) \\ &=\sum_{z} P(y \mid d o(x), z) \sum_{w} P\left(z \mid s, s^{\prime}, w\right) P\left(w \mid d o(x), s, s^{\prime}\right)\\& \quad \because \left(X \perp Z \mid S, S^{\prime}, W\right)_D \\ &=\sum_{z} P(y \mid d o(x), z) \sum_{w} P\left(z \mid s, s^{\prime}, w\right) \sum_{t} P\left(w \mid d o(x), s, s^{\prime}, t\right) P\left(t \mid d o(x), s, s^{\prime}\right)\\ &=\sum_{z} P(y \mid d o(x), z) \sum_{w} P\left(z \mid s, s^{\prime}, w\right) \sum_{t} P(w \mid d o(x), t) P\left(t \mid d o(x), s, s^{\prime}\right) \\ &\quad \because\text{$T$'s $S$-admissibility for CE of X on W} \\ &=\sum_{z} P(y \mid d o(x), z) \sum_{w} P^{*}(z \mid w) \sum_{t} P(w \mid d o(x), t) P^{*}(t) \end{aligned}$$

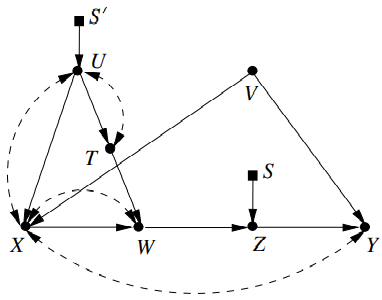
• 이 formula는 필요없는 변수들을 알아내서 learning agent가 무엇을 학습할 지를 guide해준다.

5. Transportability Across Observational Domains

이제까지의 analysis는 target domain에서 passive observation만으론 identify될 수 없어서 experimental learning이 필요하다고 가정했다.

이번 섹션에선 observational finding 간의 transport가 도움될 수 있음을 설명하겠다.

LA에서 수십개의 변수와 수천개의 sampe를 갖고서 정교한 observation study를 했다고 가정하자.

NYC에서 똑같은 대상을 estimate하고자 한다.

이 때, 바닥부터 다시 시작해야할 지에 대한 질문이 생긴다.

복잡한 모델 $P^*$의 변수 중 일부만 집중할 수 있다면 비용이 줄어들 수 있다.

---

Definition 5 (Observational Transportability)

​ Given the two domain $\Pi$ and $\Pi^{\star}$, a statistical relation $R(P)$ is said to be observational transportable $\Pi \Rightarrow \Pi^{\star}$ if

• $R(P^\star)$ is identified from $\Pi$ and $\Pi^\star(V^\star)$ where $V^\star$ is a subset of variables

---

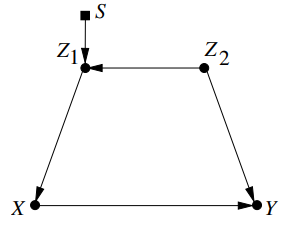
$P(x, y, z_1, z_2)$를 학습한 후에, target domain에서 $X, Y$에 대한 관측없이 $X\rightarrow Y$ classification에 관심있다.

이는 $P(y \mid x)$ is observational transportable over $V^* = \{Z_1, Z_2 \}$에 대한 질문이다.

$$P^{*}\left(x, y, z_{1}, z_{2}\right)=P\left(y \mid z_{2}, x\right) P\left(x \mid z_{1}\right) P\left(z_{2}\right) P^{*}\left(z_{1} \mid z_{2}\right)$$