0. Abstract
이 논문은 Bayesian model for causal inference의 identifiability를 확인하는 방법을 소개한다.
비록 do-calculus는 causeal graph가 주어졌을 때 sound&complete 하지만, 많은 실용적인 가정들이 표현될 수 없다.
- instrumental variable design
- regression discontinuity design
- within-subjects design
Simulation-based identifiability test를 소개하겠다.
이는 causal assumption을 SCM상의 함수들의 prior로 나타낸다.
SBI가 asymptotically sound&complete임을 증명하고 practical finite sample bound를 제공하겠다.
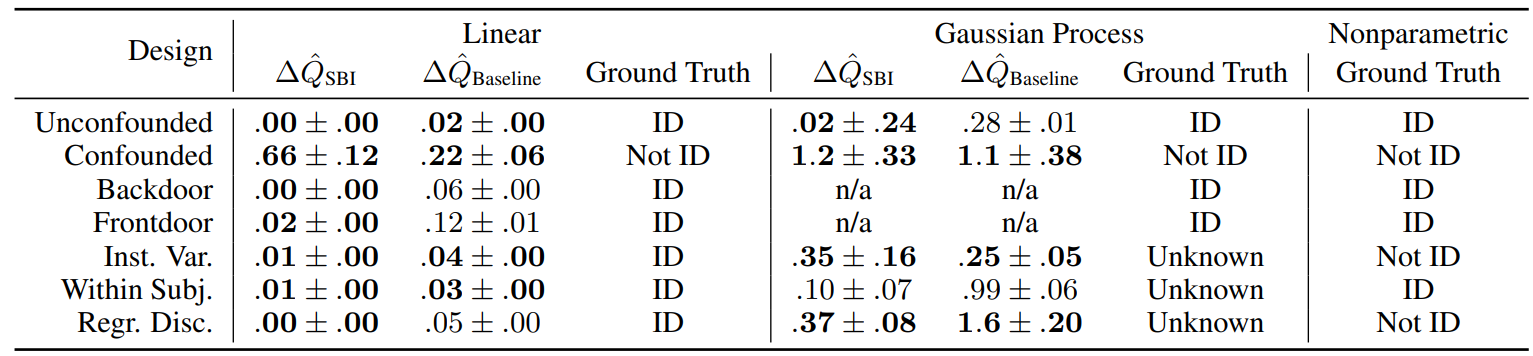
Empirical하게 SBI가 graph-based identification과 일치하는 것을 보이겠다.
1. Introduction
Causal graph가 주어졌을 때, do-calculus는 nonparametric identification에서 complte&sound procedure이다.
하지만 graph structure 단독으로는 causal knowledge의 완벽한 정보를 제공할 수 없다.
- Instrumental variable designs은 monotonicity 또는 linearity를 요구한다.
- Within-subjects designs은 unit들 간에 공유하는 latent confounder를 요구한다.
- Regression discontinuity는 do-calculus의 positivity assumption에 위배된다.
이 논문은 이에 대한 대안적인 방법을 소개한다.
- causal assumption을 SCM상의 prior로 표현하고
- likelihood가 동일하지만 effect가 다른 모델들을 찾는다.
우리는 SCM에 prior를 거는 모델들과 호환이 되는 automated identification technique인 SBI를 소개하겠다.
SBI는 causal identification 문제를 두개의 SCM 후보를 갖고서 CE를 최대한 떨어트리되, likelihood를 최대화하는 최적화 문제로 해석한다.
만약, 두 모델이 CE estimate마저 일치하게 된다면 CE가 identifiable이라는 결론이 나온다.
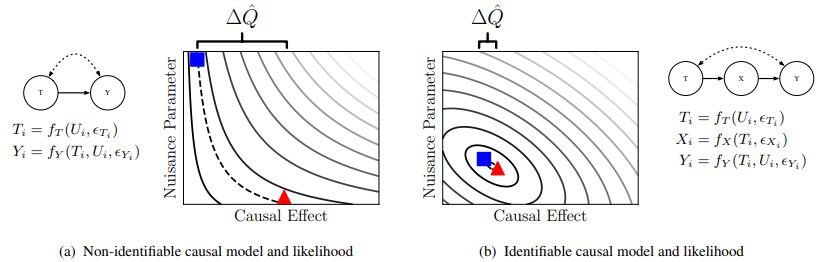
Section 4에서 SBI에 대한 증명을 할 것이고, Section 5에서 SBI가 위에서 말한 designs에 적용 가능함을 보이겠다.
그리고 Gaussian processes를 활용한 SBI의 semi-parametric extension을 소개하겠다.
Bayesian nonparametrics이라는 용어가 있음에도 semi-parametric이라 부른 이유는 nonparametric identification의 nonparametric과 확실한 구분을 위해서 라고 한다.
1.1. Related Work
Automatic Identification
- Pearl, 1995, Huang & Valtorta, 2012등 do-calculus에 기반하여 nonparametric identifiability를 결정하는 연구들이 있다.
- Bollen, 2005, Kumor, 2019 등 linear parametric identifiability 연구들이 있다.
- 그러나 이들 연구는 semi-parametric causal model(rich structure)나 non-graphical assumption에 대해 커버하지 않는다.
Likelihood equivalent parameters using gradient-based search
- Raue, 2009, Valdes-Sosa, 2011
- SBI는 이들과 달리
- particle-based objective를 사용해 single MLE보단 전역적으로 찾는다.
- 제안하는 objective function은 명시적으로 different CE를 estimate하는 모델들을 찾는다.
- 이러한 차이점은 SBI가 semi-parametric일 때나 parameter가 많은 경우에서도 올바르게 identifiability를 결정할 수 있음을 의미한다.
It is well known that causal effects can be identified even in settings where individual parameters can not (Pearl, 2009).
이게 뭔 지 잘 모르겠다.
2. Preliminaries
2.1 Structural Causal Models
SBI는 causal assumption이 SCM 상의 prior로 표현되길 요구한다.
SCM $(\mathbf F, \mathbf V, \mathbf U, P(\boldsymbol \epsilon))$은 $P\left(\mathbf{V}, \mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime}}, \mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime \prime}}\right)$의 분포를 induce한다.
$\mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime}}$은 $do(\mathbf V^\prime = \mathbf v^\prime)$을 했을 때 induce된 randomvariable을 나타낸다.
$\mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime}}, \mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime \prime}}$을 같이 joint에 묶은 이유는 counterfactuals인데 이러한 표기를 쓴 이유는 noise variable을 같게 하기 위함으로 보인다.
그래야, 다른 intervention을 줬을 때 뭐가 나왔을 것이다에 정확하게 대응됨
- $\mathbf{V} = \{ \mathbf{V}_i \}_{i=1, \cdots, n} $
- $\mathbf{U} = \{ \mathbf{U}_i \}_{i=1, \cdots, n} $
2.2 Priors over Functions
Parametric prior
$f_{y}\left(x_{i}, \epsilon_{i}\right)=\beta \cdot x_{i}+\epsilon$ 에 대해 $\beta \sim \mathcal{N}(0,1)$ 를 prior로 건다.
Semiparametric prior
Prior가 joint distribution $P\left(\mathbf{V}, \mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime}}, \mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime \prime}}\right)$으로 주어진다.
3. Identifiability in Bayesian Causal Inference
Given prior over $(\mathbf F, \mathbf U, P(\boldsymbol \epsilon))$, we are interested in $P\left(Q\left(\mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime}}, \mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime \prime}}\right) \mid \mathbf{V}\right)$
Causal effect의 posterior에 관심이 있는 경우 causal estimand $Q = \frac{1}{N}\sum_{i=1}^NY_{T=t^\prime} - Y_{T=t^{\prime \prime}}$ 일 것이다.
Let $\mathbf{F}^{\star}, \mathbf{U}^{\star}, \boldsymbol{\epsilon}^{\star} \sim P(\mathbf{F}, \mathbf{U}, \boldsymbol{\epsilon})$ be a sample from the prior.
Let $\mathbf{V}^{\star}, \mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime}}^{\star}, \mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime \prime}}^{\star}$ be observed and counterfactual random variables generated by $\mathbf{F}^{\star}, \mathbf{U}^{\star}, \boldsymbol{\epsilon}^{\star}$
Then,
Definition 3.1
Given a sample $\mathbf{F}^{\star}, \mathbf{U}^{\star}, \boldsymbol{\epsilon}^{\star}$, causal estimand $Q$ is identifiable if
the posterior $Q\left(\mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime}}, \mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime \prime}}\right) \mid \mathbf{V}^{\star}$ converges to $Q\left(\mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime}}^{\star}, \mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime \prime}}^{\star}\right)$ as $n\rightarrow \infty$
비록 정의는 posterior convergence로 주어졌으나, causal estimand가 identifiable인 지 결정하는 것은 posterior를 구하는 것을 요구하지 않는다.
대신에, conditional density를 최대화하는 함수와 confounder가 유일함으로 보인다.
Theorem 3.1
Let $\mathbf V$ be composed of $n$ i.i.d. instances.
Then, $^\forall \left(\mathbf{F}^{\dagger}, \mathbf{U}^{\dagger}\right) \in \operatorname{supp}(P(\mathbf{F}, \mathbf{U}))$, $\frac{P\left(\mathbf{V}^{\star} \mid \mathbf{F}^{\dagger}, \mathbf{U}^{\dagger}\right)}{P\left(\mathbf{V}^{\star} \mid \mathbf{F}^{\star}, \mathbf{U}^{\star}\right)} \rightarrow 1 \quad \text{or} \quad 0 \quad \text{as $n \rightarrow \infty$}$
(proof sketh)
- Let $p=\mathbb{E}\left[\frac{P\left(\mathbf{V}_{i}^{\star} \mid \mathbf{F}^{\dagger}, \mathbf{U}^{\dagger}\right)}{P\left(\mathbf{V}_{i}^{\star} \mid \mathbf{F}^{\star}, \mathbf{U}^{\star}\right)}\right]$ for a single data instance
- Then, $\mathbb{E}\left[\frac{P\left(\mathbf{V}_{i}^{\star} \mid \mathbf{F}^{\dagger}, \mathbf{U}^{\dagger}\right)}{P\left(\mathbf{V}_{i}^{\star} \mid \mathbf{F}^{\star}, \mathbf{U}^{\star}\right)}\right]=p^{n}$ for $n$ data instances.
- As $0 \leq p \leq 1$, $\lim _{n\rightarrow \infty} p^n = 0\quad \text{or} \quad 1$
- By WLLN, $\frac{P\left(\mathbf{V}^{\star} \mid \mathbf{F}^{\dagger}, \mathbf{U}^{\dagger}\right)}{P\left(\mathbf{V}^{\star} \mid \mathbf{F}^{\star}, \mathbf{U}^{\star}\right)} \rightarrow 0 \quad \text{or} \quad 1$
WLLN은 sum에 대한 수렴이라, 제대로 이해하려면 likelihood ratio convergence theorem을 봐야알 듯 하다.
Theorem 3.2
Given a sample $\mathbf{F}^{\star}, \mathbf{U}^{\star}, \boldsymbol{\epsilon}^{\star} \sim P(\mathbf{F}, \mathbf{U}, \boldsymbol{\epsilon})$, a causal estimand $Q$ is identifiable iff
$^{\not \exists} \left(\mathbf{F}^{\dagger}, \mathbf{U}^{\dagger}\right)$ s.t.
$P\left(\mathbf{V}^{\star} \mid \mathbf{F}^{\dagger}, \mathbf{U}^{\dagger}\right) \rightarrow P\left(\mathbf{V}^{\star} \mid \mathbf{F}^{\star}, \mathbf{U}^{\star}\right)$ as $n \rightarrow \infty$
and
$Q\left(\mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime}}^{\dagger}, \mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime \prime}}^{\dagger}\right) \neq Q\left(\mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime}}^{\star}, \mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime \prime}}^{\star}\right)$ where $\mathbf{V}^{\dagger}$ is the simulated result with $ \left(\mathbf{F}^{\dagger}, \mathbf{U}^{\dagger}, \boldsymbol{\epsilon}^{\star} \right)$
and
$P\left(\mathbf{F}^{\dagger}, \mathbf{U}^{\dagger}\right)>0$
(Proof)
<==
적절한 prior와 regularity condition에 대해서, Bernstein-von Mises 정리가 posterior의 consistency와 asymptotically normality를 보장한다.
==>
증명이 이해가 안되어서 sketch만 적겠다.
Let $\mathbb A^\dagger = \left\{(\mathbf{F}, \mathbf{U}) \in \operatorname{supp}(P(\mathbf{F}, \mathbf{U})): Q\left(\mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}_{1}^{\prime}}, \mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}_{2}^{\prime}}\right)= Q\left(\mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime}}^{\dagger}, \mathbf{V}_{\mathbf{V}^{\prime}=\mathbf{v}^{\prime \prime}}^{\dagger}\right) \right \}$
Let $\mathbb{L}^{\star} = \left \{(\mathbf{F}, \mathbf{U}) \in \operatorname{supp}(P(\mathbf{F}, \mathbf{U})): \frac{P\left(\mathbf{V}^{\star} \mid \mathbf{F}, \mathbf{U}\right)}{P\left(\mathbf{V}^{\star} \mid \mathbf{F}^{\star}, \mathbf{U}^{\star}\right)} \rightarrow 1 \text { as } n \rightarrow \infty\right\}$
WTS, $Q$ is identifiable $\Rightarrow$ $P \left( \sim \mathbb A^\dagger \cap \mathbb L^\star \mid \mathbf V^\star\right) \rightarrow 0$
Since $Q$ is identifiable iff $P \left( \sim \mathbb A^\dagger \mid \mathbf V^\star\right) \not \rightarrow 0$ by definition 3.1, it’s all done.
Theorem 3.2는 identifiability를 multiple maximum likelihood SCM의 CE가 같은 지 여부로 연관시켜서 SBI procedure를 제공한다.
대우로 사용해선 안된다고 한다.
이 부분은 정확하게 이해가 안됨
4. Simulation-Based Identifiability
Consider the following objective function
where $\Delta Q=\left|Q^{1}-Q^{2}\right|$ is the difference of causal estimates of two SCMs.
Let $\hat{\mathbf{F}}^{1}, \hat{\mathbf{U}}^{1}, \hat{\mathbf{F}}^{2}, \hat{\mathbf{U}}^{2} = \arg\max \mathcal{L}\left(\mathbf{F}^{1}, \mathbf{U}^{1}, \mathbf{F}^{2}, \mathbf{U}^{2}; \mathbf{V}^{\star}\right)$
Let $\Delta \hat{Q}$ be the corresponding $\Delta Q$
Theorem 4.1 (Two SCMs converge to MLE solutions)
$^{\forall}\mathbf V^\star \sim P(\mathbf V \mid \mathbf F^\star, \mathbf U ^{\star})$, $P\left(\mathbf{V}^{\star} \mid \hat{\mathbf{F}}^{i}, \hat{\mathbf{U}}^{i}\right) \rightarrow P\left(\mathbf{V}^{\star} \mid \mathbf{F}^{\star}, \mathbf{U}^{\star}\right) \quad \text{as $n\rightarrow \infty$}$ for $i=1, 2$
(Proof)
WLOG, toward a contradiction, assume that $P\left(\mathbf{V}^{\star} \mid \hat{\mathbf{F}}^{1}, \hat{\mathbf{U}}^{1}\right) \not \rightarrow P\left(\mathbf{V}^{\star} \mid \mathbf{F}^{\star}, \mathbf{U}^{\star}\right)$
By theorem 3.1, $\frac{P\left(\mathbf{V}^{\star} \mid \hat{\mathbf{F}}^{1}, \hat{\mathbf{U}}^{1}\right)}{P\left(\mathbf{V}^{\star} \mid \mathbf{F}^{\star}, \mathbf{U}^{\star}\right)} \rightarrow 0 \text { as } n \rightarrow \infty$
Then, $\mathcal{L}\left(\mathbf{F}^{\star}, \mathbf{U}^{\star}, \mathbf{F}^{\star}, \mathbf{U}^{\star}, \mathbf{V}^{\star}\right) > \mathcal{L}\left(\hat{\mathbf{F}}^{1}, \hat{\mathbf{U}}^{1}, \hat{\mathbf{F}}^{2}, \hat{\mathbf{U}}^{2}, \mathbf{V}^{\star}\right) \rightarrow -\infty \quad \text{as $n \rightarrow \infty$}$
It contradicts to $\hat{\mathbf{F}}^{1}, \hat{\mathbf{U}}^{1}, \hat{\mathbf{F}}^{2}, \hat{\mathbf{U}}^{2} = \arg\max \mathcal{L}\left(\mathbf{F}^{1}, \mathbf{U}^{1}, \mathbf{F}^{2}, \mathbf{U}^{2}; \mathbf{V}^{\star}\right)$
Let $\mathbb L$ be the set of maximum likelihood functions and latent confounders, $(\mathbf F , \mathbf U)$
Theorem 4.2
$\Delta \hat{Q} \rightarrow \max _{\left(\mathbf{F}^{1}, \mathbf{U}^{1}, \mathbf{F}^{2}, \mathbf{U}^{2}\right) \in \mathbb{L}} \Delta Q \quad \text{as $n \rightarrow \infty$ }$
(Proof)
Toward a contradiction, assume that $^{\exists}\left(\mathbf{F}^{1}, \mathbf{U}^{1}, \mathbf{F}^{2}, \mathbf{U}^{2}\right)$ s.t. $\mathcal{L}\left(\mathbf{F}^{1}, \mathbf{U}^{1}, \mathbf{F}^{2}, \mathbf{U}^{2}, \mathbf{V}^{\star}\right) = \mathcal{L}\left(\hat{\mathbf{F}}^{1}, \hat{\mathbf{U}}^{1}, \hat{\mathbf{F}}^{2}, \hat{\mathbf{U}}^{2}, \mathbf{V}^{\star}\right)$ and $\left|Q^{1}-Q^{2}\right| >\left|\hat{Q}^{1}-\hat{Q}^{2}\right|$
By theorem 4.1, $P\left(\mathbf{V}^{\star} \mid \mathbf{F}^{1}, \mathbf{U}^{1}\right), P\left(\mathbf{V}^{\star} \mid \mathbf{F}^{2}, \mathbf{U}^{2}\right), P\left(\mathbf{V}^{\star} \mid \hat{\mathbf{F}}^{1}, \hat{\mathbf{U}}^{1}\right), P\left(\mathbf{V}^{\star} \mid \hat{\mathbf{F}}^{2}, \hat{\mathbf{U}}^{2}\right)$ all converge to $P\left(\mathbf{V}^{\star} \mid \mathbf{F}^{\star}, \mathbf{U}^{\star}\right) \text { as } n \rightarrow \infty$
$\mathcal{L}\left(\mathbf{F}^{1}, \mathbf{U}^{1}, \mathbf{F}^{2}, \mathbf{U}^{2}, \mathbf{V}^{\star}\right) \rightarrow 2 \log P\left(\mathbf{V}^{\star} \mid \mathbf{F}^{\star}, \mathbf{U}^{\star}\right)+\left|Q^{1}-Q^{2}\right| = 2 \log P\left(\mathbf{V}^{\star} \mid \mathbf{F}^{\star}, \mathbf{U}^{\star}\right) +\left|\hat{Q}^{1}-\hat{Q}^{2}\right|$ is contradiction to $\left|Q^{1}-Q^{2}\right| >\left|\hat{Q}^{1}-\hat{Q}^{2}\right|$
Theorem 4.1 덕분에, $n$이 무한대로 감에 따라서 maximizer 중에서 MLE가 아닌 애가 있다는 것에 모순이 생김
Theorem 4.3
Given a prior $P(\mathbf{F}, \mathbf{U}, \boldsymbol{\epsilon})$ and a sample $\mathbf{F}^{\star}, \mathbf{U}^{\star}, \boldsymbol{\epsilon}^{\star}$ from that prior, a causal estimand $Q$ is identifiable iff
$\Delta \hat{Q} \rightarrow 0 \text { as } n \rightarrow \infty$
(Proof)
Theorem 4.1 : $\left(\hat{\mathbf{F}}^{1}, \hat{\mathbf{U}}^{1}\right) , \left(\hat{\mathbf{F}}^{2}, \hat{\mathbf{U}}^{2}\right) \in \mathbb L^{\star}$
Theorem 4.2 : $ \hat \Delta Q $ maximizes the distance between induced causal estimates
$\Delta \hat{Q} \rightarrow 0$ implies $^{\not \exists} \left(\hat{\mathbf{F}}^{i}, \hat{\mathbf{U}}^{i}\right) \in \sim \mathbb A^{\dagger}$

Assumption 4.1
Let $\mathbb{E}_{\mathbf{V}^{\star}, n} \Delta \hat{Q}$ denote the expected difference between causal estimates for $n$ instances.
Assume that $\mathbb{E}_{\mathbf{V}^{\star}, n} \Delta \hat{Q} \geq \mathbb{E}_{\mathbf{V}^{\star}, \infty} \Delta \hat{Q}$ for all $n \in \mathbb N$
받아들일 만한 가정이다.
finite sample의 문제로 likelihood ratio과 0또는 1로 충분히 수렴하지 못했을 수 있다.
비록 $Q$가 identifiable일 지라도, $\mathbb L^\star$의 느슨해진 범위로 인해 $\Delta \hat Q$을 키울 기회가 생길 수 있다.
$Q$가 not identifiable인 경우는 $\Delta \hat Q$이 크게 나올 것이므로 알고리즘이 이 가정이 틀릴 수 있어도 False를 뱉을 것이다.
Theorem 4.4
If Algorithm 1 returns TRUE, $P\left(\mathbb{E}_{\mathbf{V}^{\star}, \infty} \Delta \hat{Q}>t\right)<p$
Selecting the repulsion strength
- $P\left(\mathbf{V}^{\star} \mid \hat{\mathbf{F}}^{1}, \hat{\mathbf{U}}^{1}\right)$와 $P\left(\mathbf{V}^{\star} \mid \hat{\mathbf{F}}^{2}, \hat{\mathbf{U}}^{2}\right)$가 충분히 다르다면, $\lambda$는 감소되어야한다.
4.1. Example: Confounded GP Regression
Consider a SCM over
- observed $\mathbf{V}=\left\{T_{1}, Y_{1}, \ldots, T_{n}, Y_{n}\right\}$
- unobserved $\mathbf U = \left\{U_{1}, \ldots, U_{n}\right\}$
Assume that
- $Y_{i}=f\left(T_{i}, U_{i}\right)$ is drawn from
- $f \sim GP(0, k(\cdot, \cdot ))$ where $k\left(\left[T_{i}, U_{i}\right],\left[T_{j}, U_{j}\right]\right)=k\left(T_{i}, T_{j} ; l_{T}, s_{T}\right) \cdot k\left(U_{i}, U_{j} ; l_{U}, s_{U}\right)$
- with additive exogeneous noise
- $T_{i}=\gamma \cdot U_{i}+\epsilon_{T_{i}}$
Let $K_{U}, K_{T}, K_{T, t^{\prime}}$ and $K_{T, t^{\prime \prime}}$ be $n \times n$ matrices s.t. $(i,j)$ elements are given by
- $k\left(U_{i}, U_{j} ; l_{U}, s_{U}\right)$
- $k\left(T_{i}, T_{j} ; l_{T}, s_{T}\right)$
- $k\left(T_{i}, t^{\prime} ; l_{T}, s_{T}\right)$
- $k\left(T_{i}, t^{\prime \prime} ; l_{T}, s_{T}\right)$
Let $\mathbf 1$ be a $n\times n$ block matrix of ones.
Optimize over $\mathbf F$ involves
- $\theta=\left\{l_{T}, s_{T}, l_{U}, s_{U}, \gamma, \sigma_{T}^{2}, \sigma_{Y}^{2}\right\}$
- inducing counterfactual outcomes $\mathbf{y}_{\mathrm{cf}}=\left[\mathbf{y}^{\prime}, \mathbf{y}^{\prime \prime}\right]$
where
Let $Q = \frac{1}{n} \sum_{i \in n} \mathbf{y}_{i}^{\prime}-\mathbf{y}_{i}^{\prime \prime}$
Then,
나머지도 closed form으로 구했는데 이들은 automatic differentiation으로 구할 수 있다.
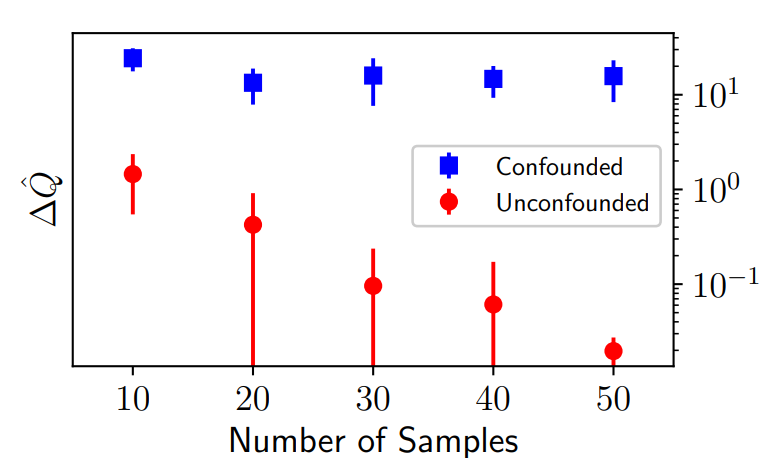
Confounded model은 identifiable하지 않음을 나타낸다.
5. Experiments