0. Abstract

IPMs는 data를 modeling하는 flexible class이다.

이는 observation을 simulate할 수 있는 process이다.

GAN 처럼 likelihood를 몰라도 된다.

이 논문에선 HIMs와 DIMs를 도입한다.

DNN을 사용하여 HBM with implicit density를 정의한다.

IPM을 쓰는 경우 일반적으로 accurate & scalable inference는 어렵다.

우리는 model의 implicity도 허용하면서 A&S posterior inference도 혀용한다.

1. Introduction

Coin toss modeling을 간단하게 할 수 있다.

$p \sim \text{Beta}(a,b)$
$X \sim \text{Ber}(p)$
$p | X \sim \text{Beta}(a’, b’)$

하지만 각도 세기 등의 initial parameter의 noisy로 coin toss에 randomness가 생긴 것이다.

IM은 이러한 것들을 담는다.

IM이란 표현은 simulator로도 알려져 있다.

IM으로 부터 sampling은 가능하나 density를 모를 것이다.

우리는 HIMs을 도입한다.

HIM은 HBM인데 sampling은 가능하고 density는 모르는 경우이다.

이는 대부분의 simulator를 포함하고 GAN도 포함한다.

HIMs에서 추가로 LV의 생성에도 DNN으로 쌓아서 rich하게 만든 것을 DIMs라고 하겠다.

IM의 이전 연구들은 likelihood를 모르기 때문에 A&S BI에 한계가 있다.

Ratio estimation에 영감을 받아서, 새로운 VI를 개발했다.

IM을 다루는 일반적인 method는 approximate Bayesian computation (ABC) 이다.

잘은 모르겠지만 사람이 고른 summary statistics으로 가까움을 잰다고 한다.

그러나 이는 너무 사람의 선택에 의존하고 차원이 증가하면 안된다고 한다.

GAN은 NN으로 이미지를 simulate한다.

Larsen, 2016 : variational method for improved reconstruction
Chen, 2016 : disentangle factors of variation

우리는 hierarchical and deep latent structure로 posterior를 추론한다.

Design of variational family를 모델링 문제로 던지는 연구들이 있다.

2. Implicit Probabilistic Models

2.1. Hierarchical Implicit Models

HBM은 tractable likelihood $p\left(\mathbf{x}_{n} \mid \mathbf{z}_{n}, \boldsymbol{\beta}\right)$을 사용한다.

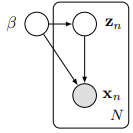
$p(\mathbf{x}, \mathbf{z}, \boldsymbol{\beta})=p(\boldsymbol{\beta}) \prod_{n=1}^{N} p\left(\mathbf{x}_{n} \mid \mathbf{z}_{n}, \boldsymbol{\beta}\right) p\left(\mathbf{z}_{n} \mid \boldsymbol{\beta}\right)$

하지만 simulator-based model과 GAN은 그렇지 않다.

그것마저 포함하는 HIM을 도입하겠다.

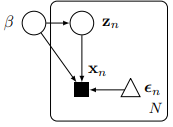
$\mathbf{x}_{n}=g\left(\boldsymbol{\epsilon}_{n} \mid \mathbf{z}_{n}, \boldsymbol{\beta}\right), \quad \boldsymbol{\epsilon}_{n} \sim s(\cdot)$

즉 함수 $g$와 noise의 분포만 명시한다.

예시

$\begin{aligned} &\frac{\mathrm{d} x_{1}}{\mathrm{~d} t}=\beta_{1} x_{1}-\beta_{2} x_{1} x_{2}+\epsilon_{1}, \quad \epsilon_{1} \sim \operatorname{Normal}(0,10) \\ &\frac{\mathrm{d} x_{2}}{\mathrm{~d} t}=-\beta_{2} x_{2}-\beta_{3} x_{1} x_{2}+\epsilon_{2}, \quad \epsilon_{2} \sim \operatorname{Normal}(0,10) \end{aligned}$
$\mathbf{x}_{n}=g\left(\boldsymbol{\epsilon}_{n} ; \boldsymbol{\theta}\right), \quad \boldsymbol{\epsilon}_{n} \sim s(\cdot)$

2.2 Deep Implicit Models

Latent variable의 $\mathbf z_n$에 간단한 노이즈를 주되 층을 쌓아서 complex density로 설정할 수 있다.

$\begin{aligned} \mathbf{z}_{n, L} &=g_{L}\left(\boldsymbol{\epsilon}_{n, L} \mid \boldsymbol{\beta}_{L}\right) & \boldsymbol{\epsilon}_{n, L} \sim s(\cdot) \\ \mathbf{z}_{n, L-1} &=g_{L-1}\left(\boldsymbol{\epsilon}_{n, L-1} \mid \mathbf{z}_{n, L}, \boldsymbol{\beta}_{L-1}\right) & \boldsymbol{\epsilon}_{n, L-1} \sim s(\cdot)\\ & \vdots \\ \mathbf{z}_{n, 1} &=g_{1}\left(\boldsymbol{\epsilon}_{n, 1} \mid \mathbf{z}_{n, 2}, \boldsymbol{\beta}_{1}\right) & \boldsymbol{\epsilon}_{n, 1} \sim s(\cdot) \end{aligned}$

이는 complex prior density를 허용한다.

VAE와 같은 구조에 바로 적용 가능한 방법이다.

Reparameterization trick을 이용하기 위해 간단하게 $g_l$은 $\boldsymbol \epsilon_l$에 대해 linear하게 둔다.

$g_{\ell}\left(\boldsymbol{\epsilon}_{n, \ell} \mid \mathbf{z}_{n, \ell+1}, \beta_{\ell}\right)=\mu\left(\mathbf{z}_{n, \ell+1}, \beta_{\ell}\right)+\sigma\left(\mathbf{z}_{n, \ell+1}, \beta_{\ell}\right) \boldsymbol{\epsilon}_{n, \ell}$

3. Variational Inference for Implicit Models

Posterior $p(\mathbf{z}, \boldsymbol{\beta} \mid \mathbf{x})=p(\mathbf{x}, \mathbf{z}, \boldsymbol{\beta}) / p(\mathbf{x})$ 를 구하고 싶으나 marginal distribution 뿐만 아니라 joint distribution도 모르는 상황이다.

VI로 posterior를 approximate하려고 한다. VI에 다양한 버전이 있다.

Objective를 고르는 데에 있어서, 바라는 것들을 나열해보면,

Scalability
- 미니 배치 단위의 subsampling으로 true objective를 unbiased estimate 할 수 있어야 한다.
- $\sum_{n=1}^{N} f\left(\mathbf{x}_{n}\right) \approx \frac{N}{M} \sum_{m=1}^{M} f\left(\mathbf{x}_{m}\right)$
Implicit Local Approximations
- IM 자체가 $\mathbf z \rightarrow \mathbf x$를 flexible density로 명시하기에
- $\mathbf z \mid \mathbf x$의 분포도 complex density를 가질 것이다.
- 그렇기에 variational family에도 richness를 주고 싶다.
- 즉, $q\left(\mathbf{z}_{n} \mid \mathbf{x}_{n}, \boldsymbol{\beta}\right)$가 뭔 지 몰라도 뽑을 수 있으면 된다는 objective를 원한다.

3.1 KL Variational Objective

VI의 classic form은 variational distribution을 posterior에 붙이는 것이다.

이는 ELBO를 maximization 하는 것과 동일하다.

$\mathcal{L}=\mathbb{E}_{q(\boldsymbol{\beta}, \mathbf{z} \mid \mathbf{x})}[\log p(\mathbf{x}, \mathbf{z}, \boldsymbol{\beta})-\log q(\boldsymbol{\beta}, \mathbf{z} \mid \mathbf{x})]$

Let $q$ factorize

$q(\boldsymbol{\beta}, \mathbf{z} \mid \mathbf{x})=q(\boldsymbol{\beta} \mid \mathbf{x}) \prod_{n=1}^{N} q\left(\mathbf{z}_{n} \mid \mathbf{x}_{n}, \boldsymbol{\beta}\right)$

where $q\left(\mathbf{z}_{n} \mid \mathbf{x}_{n}, \boldsymbol{\beta}\right)$ is an intractable density.

$\begin{aligned} \mathcal{L}=&\mathbb{E}_{q(\boldsymbol{\beta} \mid \mathbf{x})}[\log p(\boldsymbol{\beta})-\log q(\boldsymbol{\beta} \mid \mathbf{x})] \\ &+\sum_{n=1}^{N} \mathbb{E}_{q\left(\boldsymbol{\beta}, \mathbf{z}_{n} \mid \mathbf{x}\right)}\left[\log p\left(\mathbf{x}_{n}, \mathbf{z}_{n} \mid \boldsymbol{\beta}\right)-\log q\left(\mathbf{z}_{n} \mid \mathbf{x}_{n}, \boldsymbol{\beta}\right)\right] \end{aligned}$

Classifc objective는 $p\left(\mathbf{x}_{n}, \mathbf{z}_{n} \mid \boldsymbol{\beta}\right)$와 $q\left(\mathbf{z}_{n} \mid \mathbf{x}_{n}, \boldsymbol{\beta}\right)$가 intractable이라 어렵다.

3.2 Ratio Estimation for the KL Objective

Let $q\left(\mathbf{x}_{n}\right)$ be the empirical distribution on the observations $\mathbf x$

이걸 어떻게 구하는 지 모르겠다.

고차원 데이터에선 더더욱 어렵지 않나??

Then,

$\begin{aligned} \mathcal{L}:=& \mathcal L - \sum_{n=1}^N \log q (\mathbf x_n) \\ = & \mathbb{E}_{q(\boldsymbol{\beta} \mid \mathbf{x})}[\log p(\boldsymbol{\beta})-\log q(\boldsymbol{\beta} \mid \mathbf{x})] + \sum_{n=1}^{N} \mathbb{E}_{q(\boldsymbol{\beta} \mid \mathbf{x}) q\left(\mathbf{z}_{n} \mid \mathbf{x}_{n}, \boldsymbol{\beta}\right)}\left[\log \frac{p\left(\mathbf{x}_{n}, \mathbf{z}_{n} \mid \boldsymbol{\beta}\right)}{q\left(\mathbf{x}_{n}, \mathbf{z}_{n} \mid \boldsymbol{\beta}\right)}\right] \end{aligned}$

Ratio estimator를 proper scoreing rule로 알려진 loss function을 최소화하여 학습할 수 있다.

$\begin{aligned} \mathcal{D}_{\log }=&\mathbb{E}_{p\left(\mathbf{x}_{n}, \mathbf{z}_{n} \mid \boldsymbol{\beta}\right)}\left[\log \sigma\left(r\left(\mathbf{x}_{n}, \mathbf{z}_{n}, \boldsymbol{\beta} ; \boldsymbol{\theta}\right)\right)\right] \\ + &\mathbb{E}_{q\left(\mathbf{x}_{n}, \mathbf{z}_{n} \mid \boldsymbol{\beta}\right)}\left[\log \left(1-\sigma\left(r\left(\mathbf{x}_{n}, \mathbf{z}_{n}, \boldsymbol{\beta} ; \boldsymbol{\theta}\right)\right)\right)\right] \end{aligned}$

$\sigma$는 sigmoid function이고 $r$은 $p\left(\mathbf{x}_{n}, \mathbf{z}_{n} \mid \boldsymbol{\beta}\right)$에서 나왔을 확률에 대한 logit function이다.

$\mathcal{D}_{\log }$ loss가 0인 경우

$p\left(\mathbf{x}_{n}, \mathbf{z}_{n} \mid \boldsymbol{\beta}\right)$에서 나왔을 때 $\sigma(r)$이 1이고
and
$q\left(\mathbf{x}_{n}, \mathbf{z}_{n} \mid \boldsymbol{\beta}\right)$에서 나왔을 때 $\sigma(r)$이 0일 때

$r$이 충분히 expressivie하다면, optimal function은 구하고자하는 함수가 된다.

$r^{*}\left(\mathbf{x}_{n}, \mathbf{z}_{n}, \boldsymbol{\beta}\right)=\log p\left(\mathbf{x}_{n}, \mathbf{z}_{n} \mid \boldsymbol{\beta}\right)-\log q\left(\mathbf{x}_{n}, \mathbf{z}_{n} \mid \boldsymbol{\beta}\right)$

이는 $\mathcal D _{\log}$가 $r$에 대해 convex한 지와 언제 미분이 0이 되는 지로 확인 가능하다.

3.3. Stochastic Gradients of the KL Objective

Reparameterization trick

3.4. Algorithm

$\boldsymbol \theta$ update는 risk ratio estimator를 학습하는 것이고
$\boldsymbol \lambda, \boldsymbol\phi$ update는 variational approximation을 하는 것이다.

Model의 parameter인 $\boldsymbol \beta$는 상수로 두고 update를 한다.

$q(\boldsymbol \beta) := \delta_{\boldsymbol \beta}$

이러한 방식은 variational EM에 대응한다.

3.5 The KL Uniqueness Theorem

Scalability와 d implicit local approximation을 만족하는 다른 objective function이 있을까?

Theorem 1 (Uniqueness Theorem)

KLD is unique divergenvce satisfying our desiderata.

4. Experiments

4.1. Stability of Ratio Estimator

KL-divergence를 활용한 VI와 다른 점은 ratio estimation이 포함됐다는 것이다.

Ratio estimator의 accuracy를 재고 싶다.

이를 tractable case에 적용해서 확인할 수 있다.

$r^{*}(\mathbf{x}, \boldsymbol{\beta})=\log p(\mathbf{x} \mid \boldsymbol{\beta})-\log q(\mathbf{x})$

가 무엇인 지 아는 상황이다.

$r^{*}(\mathbf{x}, \boldsymbol{\beta}) - \log p(\mathbf{x} \mid \boldsymbol{\beta}) = -\log q(\mathbf{x}) = -\sum_{n} \log q\left(\mathbf{x}_{n}\right)$ 는 $\boldsymbol \beta$의 값에 변화에 흔들리지 않는다.

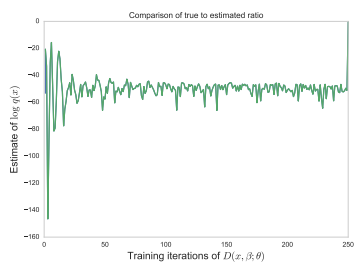
그러므로 $r$이 정확하게 estimate한다면, $r(\mathbf{x}, \boldsymbol{\beta}) - \log p(\mathbf{x} \mid \boldsymbol{\beta}) $는 $\boldsymbol \beta$의 값의 변화에 크게 흔들리지 않는다.

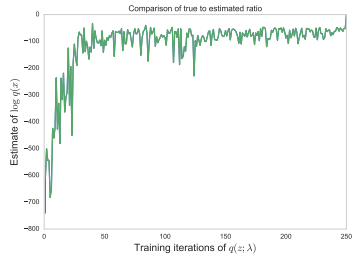
$q$가 posterior에 수렴하면서 $r(\mathbf{x}, \boldsymbol{\beta}) - \log p(\mathbf{x} \mid \boldsymbol{\beta}) $이 정확해지는 것을 볼 수 있다.

이를 확인하기 위해 $\boldsymbol \beta$를 update 안하고 ratio estimator만 학습하면

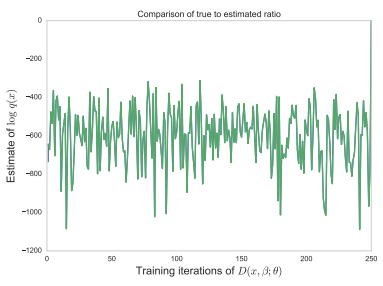
$q( \boldsymbol \beta)$를 처음부터 true값에 놓는다면 update 몇번 만에 바로 안정된다.

Study Repo

Deep and Hierarchical Implicit Models