수학적으로 들어가면 끝도 없을 것 같아서 엄밀성은 없음을 미리 고지
학습이 왜 되는 지에 대해서 느끼는 게 목적
자세히 읽으면 보완할 예정
0. Summary
- Problem
- Inference on a low dimensional parameter $\theta_0$
- in the presence of high dimensional parameter $\eta_0$
- Our approach
- $\eta_0$을 위해 ML method로 처리
- 문제
- ML method는 오버피팅을 막기 위해 regularization bias를 추가한다.
- 그러한 $\hat \eta$으로 만든 $\hat \theta$은 heavy bias를 갖는다.
- $\hat \theta$은 $N^{-\frac{1}{2}}-$consistency를 만족하지 못한다.
- 해결책
- Neyman-orthogonal score(NOS)
- nuisance parameter에 대해 sensitivity를 줄이기에,
- $\hat \eta$이 $N^{-\frac{1}{2}}-$을 만족 못해도 됨
- Cross-fitting
- 같은 샘플로 $\hat \eta$, $\hat \theta$를 학습했을 때의 상관관계를 제거하기 위함
- Neyman-orthogonal score(NOS)
- 보이게 되는 것
- $\hat \theta$
- $N^{-\frac{1}{2}}-$consistency
- asymptotically normal distribution
- unbiased
- $\hat \theta$
1. INTRODUCTION AND MOTIVATION
1.1. Motivation
Example 1.1
- $X = (X_1, \ldots, X_p)$
- $D= m_0(X) + V$
- $\mathbb E[V \mid X] = 0$
- $Y = D\theta_0 + g(X) + U$
- $\mathbb E[U \mid X, D ] = 0$
- $p$가 고차원일 때,
- ML 메소드를 써서
- nuisance parameter space의 엔트로피가 sample이 늘어감에 따라 늘어가는 방식 채택
- $\eta_0 = (m_0, g_0)$
Regularization Bias
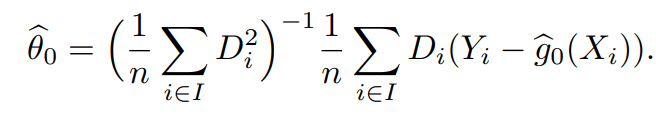
- $\mid \sqrt n (\hat \theta - \theta_0) \mid \rightarrow _P \infty$
- $N^{-\frac{1}{2}}-$consistency를 만족하지 못함
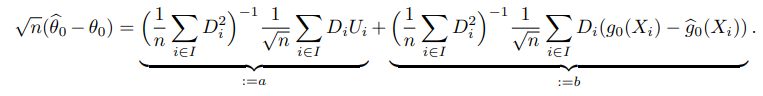
- $b$텀이 regularization bias로 인해 발산하게 된다.
- 특히, ML 메소드는 $\hat g$이 대부분 $N^{-\frac{1}{4}}-$consistency
Overcoming Regularization Biases using Orthogonalization
- $D$에서 $X$의 영향을 지우는 방식으로 orthogonalized regressor를 얻자
- $I^c$로 부터 학습한 $\hat m_0$를 갖고서
- $I$ 샘플들에 $\hat V_i = D_i - \hat m_0(X_i)$로 변환하고
- $-\hat Y_i$
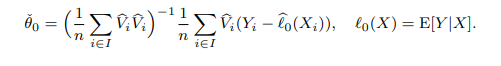
- $\hat V_i$의 기댓값이 0이라 기존 문제가 해결된다.
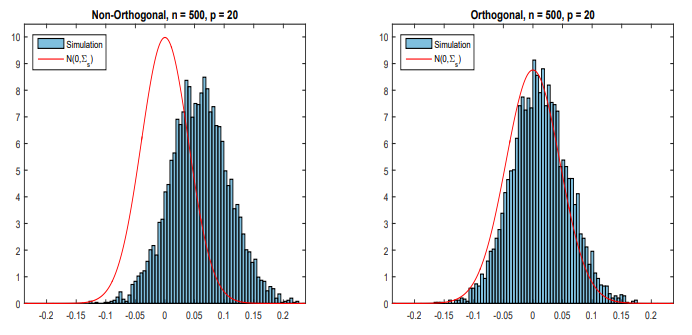
- 이제 해야할 것은 orthogonalization의 원리를 이해하는 것이다.
2. CONSTRUCTION OF NEYMAN ORTHOGONAL SCORE/MOMENT FUNCTION
2.1 Moment Condition/Estimating Equation Framework
- $\psi = (\psi_1, \ldots, \psi_{d_\theta})^\prime$
- vector of known score functions
- $\theta_0$
- true target parameter
- $\eta_0$
- true nuisance parameter
- $\mathcal T_N$
- nuisance realization set
- is a properly shrinking neighborhood of $\eta_0$
- $\theta_0$ satisfies the moment condition
- $\mathbb E_P [\psi(W; \theta_0, \eta_0)] = 0$
- $W \sim P$
- $\mathbb E_P [\psi(W; \theta_0, \eta_0)] = 0$
- Score $\psi$ is said to be NOS if
- $\partial_\eta \mathbb E_P [\psi(W; \theta_0, \eta)] = 0$
- $\eta \approx \eta_0$ 일 때
- $\partial_\eta \mathbb E_P [\psi(W; \theta_0, \eta)] = 0$
2.2 Construction of Neyman Orthogonal Scores
후보1 : log-likelihood function w.r.t. $W$
- $\psi = \frac{\partial l}{\partial \theta}$ 로 둘 경우, $\theta_0$는 moment condtion을 만족하나
- 일반적으로 NOS 조건을 만족하지 못한다.
NOS example (see Lemma 2.1)
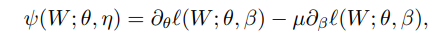
- $\mu = J_{\theta \beta} J_{\beta\beta}^{-1}\in \mathbb R^{d_\theta \times d_\beta}$
- invertible =>
- $\eta = (\beta, \text{vec}(\mu))$
- $J$
- Jacobian of log-likelihood w.r.t. $(\theta, \beta)$
- $\mu = J_{\theta \beta} J_{\beta\beta}^{-1}\in \mathbb R^{d_\theta \times d_\beta}$
위에서 구한 NOS를 Example 1.1에 적용할 경우
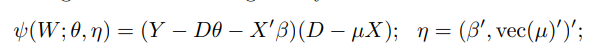
2.2.3. NOS for Likelihood
- $\mathcal B$ 를 set of functions로 가정
- Let $\ell(W; \theta, \beta)$ be a known criterion function
- $\eta$로 안쓰고 $\beta$로 쓰는 이유는 nuisance에 $\theta$ 관련된게 포함되어서
- Let $\beta_\theta = \arg \max _{\beta \in \mathcal B} \mathbb E_P(l(W; \theta, \beta))$
- Consider $\psi = \frac{d \ell(W; \theta, \eta(\theta))}{d\theta}$
- $\eta_0 (\theta) = \eta_0$
- 적절한 $l$에 대해 $\psi$ 는 NOS를 만족한다. (see Lemma 2.5)
위에서 구한 NOS를 Example 1.1에 적용할 경우
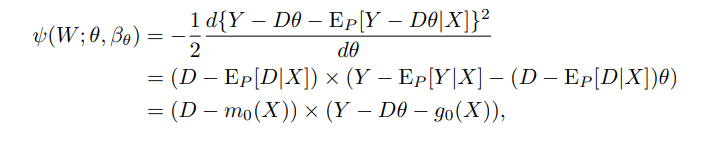
2.2.4 NOS for Conditional Moment Restriction
- Let $Z, R, W$ be random vectors w/ $d_z \leq d_r \leq d_w$
- $Z \subset R \subset W$
- Let $h_0$ be a vector-values functional nuisance parameter
- $\mathcal Z \rightarrow \mathbb R^{d_h}$
- Score function $\psi = m(W; \theta_0, h_0(Z)) \mid R$
- 이는 likelihood 명시가 없어서 rich model을 커버한다
- Lemma 2.6 says
- moment condition + Lp-norm are finite for all $h \in \mathcal H$
- 위의 조건이 만족됐을 때, $\psi$는 NOS다.
위에서 구한 NOS를 Example 1.1에 적용할 경우
- $m(W; \theta_0, \nu) = Y-D\theta - \nu$ 로 둔다면,
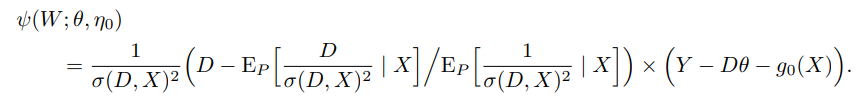
- 이 나오는 데 $Y$의 noise의 분산이 estimate안되어서 $1$로 fix하면
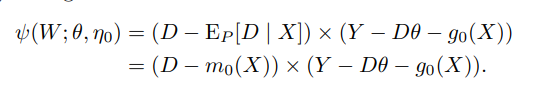
- 효율성은 떨어지는 편이다.
3. DML
3.1 Definition of DML and Its Basic Properties
Definition 3.1 (DML1)
K-fold random partition $(I_k)_{k=1}^K$ w/ size $n = \frac{N}{K}$
For each $k$
Construct the estimator $\tilde \eta_{0, k} = \hat \eta_0(W_i)_{i \in I_k^c}$
Construct the estimator $\tilde \theta_{0, k}$ as the solution of $\mathbb E_{n,k} [\psi(W; \tilde \theta_{0, k}, \tilde \eta_{0, k})] = 0$
where
- $\psi$ : NOS
- $\mathbb E_{n, k}$ : Empirical expectation over the $k$-th fold
Aggregate the estimators
- $\tilde\theta_0 = \frac{1}{K}\sum_{k=1}^K \tilde \theta_{0, k}$
Definition 3.2 (DML2)
K-fold random partition $(I_k)_{k=1}^K$ w/ size $n = \frac{N}{K}$
For each $k$
Construct the estimator $\tilde \eta_{0, k} = \hat \eta_0(W_i)_{i \in I_k^c}$
Construct the estimator $\tilde \theta_{0}$ as the solution of
$\frac{1}{K} \sum_{k=1}^K\mathbb E_{n,k} [\psi(W; \tilde \theta_{0}, \tilde \eta_{0, k})] = 0$
where
- $\psi$ : NOS
- $\mathbb E_{n, k}$ : Empirical expectation over the $k$-th fold
$\tilde \theta_0$는 $N^{-\frac{1}{2}}-$consistency를 만족한다.
3.2 Moment Condition Models with Linear Scores
- Let $c_0 >0$, $c_1 > 0$, and $c_0\leq c_1$
- Let $s> 0$ and $q>2$
- Let $\{\delta_N \}_{N\geq 1}$ and $\{\Delta_N \}_{N\geq 1}$ be positive sequences converging to zero
- Let $K \geq 2$ be some fixed integer
- Let $\{ \mathcal P_N\}_{N\geq 1}$ be some sequence of set of probability dist $P$ of $W$
Assumption 3.1 (Linear Scores with Approximate Neyman Orthogonality)
- $^{\forall}N \geq 3$ and $P \in \mathcal P_N$
- $\theta_0$ satisfies moment cond
- $\psi(w; \theta, \eta) = \psi^a(w; \eta) \theta + \psi^b(w; \eta)$
- linearity
- $\mathbb E_P[\psi (W; \theta, \eta)]$ is twice continuously diffble w.r.t. $\eta$
- smoothness
- singular values of $J_0:= \mathbb E_P[\psi^a(W; \eta_0)]$ are between $c_0$ and $c_1$
- Orthogonality
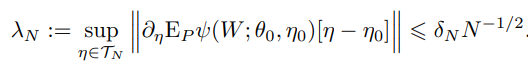
Assumption 3.2 (Score Regularity and Quality of Nuisance Parameter Estimators)
$^{\forall}N \geq 3$ and $P \in \mathcal P_N$
Given random $I \subset [N]$ w/ size $n = \frac{N}{K}$
- $\hat \eta_0 \in \mathcal T_N$ w/ pbt $1-\Delta_N$
where $\mathcal T_N$
- $\eta_0 \in \mathcal T_N$
- $m_N := \sup_{\eta \in \mathcal T_N} (\mathbb E_P [| \psi(W; \theta_0, \eta)|^q])^{\frac{1}{q}} \leq c_1$
- $m_N^\prime := \sup_{\eta \in \mathcal T_N} (\mathbb E_P [| \psi^a(W; \eta)|^q])^{\frac{1}{q}} \leq c_1$
statistical rates $r_N$, $r_N^\prime$, and $\lambda_N^\prime$ hold:
All eigenvalues of the matrix are bounded from below by $c_0$
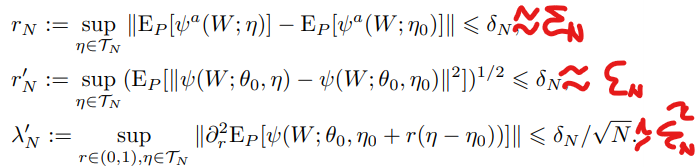
만약 $\psi$가 smooth할 경우
$\epsilon_N$은 $\hat\eta_0$의 수렴속도와 관련있으며 대부분의 ML 메소드는 $\epsilon_N = o(N^{-\frac{1}{4}})$
Theorem 3.1. (Properties of the DML)
If $\delta_N \geq N^{-\frac{1}{2}}$,
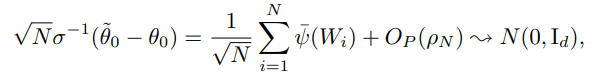
- orthogonal score에 기반한 estimator가 $\sqrt N$-consistent를 만족함을 의미한다.
Theorem 3.2. (Variance Estimator for DML)
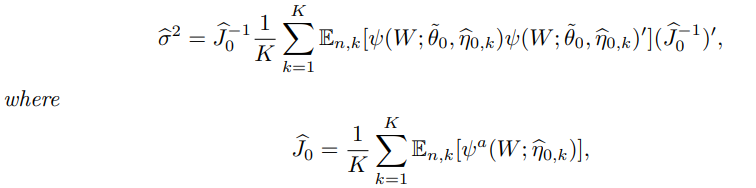
Corollary 3.1. (Uniformly Valid Confidence Bands)
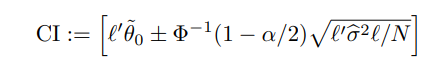
3.3. Models with Nonlinear Scores
보강예정
3.4. Finite-Sample Adjustments to Incorporate Uncertainty Induced by Sample Splitting
보강예정