Neural Combinatorial Optimization With Reinforcement Learning

0. Abstract

이 논문은 Deep RL로 CO문제를 푸는 framework를 제안한다.

1. Introduction

CO는 CS의 근본적인 문제로 이들은 다양한 분야에서 적용된다.

TSP 해 찾기는 NP-hard이다.

Heuristic work등이 있지만, condition의 변화에 적용이 불가능해진다.

반대로 ML은 heuristic을 training data에서 자동으로 찾기 때문에 다양한 condition에 적용될 수 있다.

지도학습의 label에 대한 요구로 인해 대부분의 CO에 적용되기 어렵다.

우리는 SL보다 RL이 generalization이 더 좋음을 실험적으로 보인다.

1. Policy gradient approach
   • Policy is parameterized by RNN
   • At test time, inference by greedy sampling
2. Active search
   • Search 동안의 좋은 solution들을 유지하면서 최적화??
3. 혼합

NCO는 pointer network의 지도학습 방법보다 더 낫다.

2. Previous work

TSP를 근사적으로 푸는 heuristic들이 있었다.

이보다 더 일반적인 문제인 Google’s vehicle routing problem도 있다.

No Free Lunch theorem : 다양한 search 알고리즘들은 모든 문제를 고려하게 될 경우 거기서 거기다.

결국 사전 지식에 기반해서 문제 상황에 적절한 것을 골라야 한다.

---

최근 Pointer Network가 뉴럴넷 기반으로 이 문제를 다뤘다.

3. Neural Network Architecture For TSP

• $n$ : number of cities
• $s=\left\{\mathbf{x}_{i}\right\}_{i=1}^{n}$ where $\mathbf{x}_{i} \in \mathbb{R}^{2}$
• $\pi \in \pi(s)$ : permutation of $s$
• $L(\pi \mid s)=\left|\mathbf{x}_{\pi(n)}-\mathbf{x}_{\pi(1)}\right|_{2}+\sum_{i=1}^{n-1}\left|\mathbf{x}_{\pi(i)}-\mathbf{x}_{\pi(i+1)}\right|_{2}$
• $p(\pi \mid s)=\prod_{i=1}^{n} p(\pi(i) \mid \pi(<i), s)$

Vanilla sequence to sequence 문제는 output dictionary size가 고정되어 있다.

다양한 $n$에 적용하기 위해, pointer network approach를 적용하였다.

3.1 Architecture details

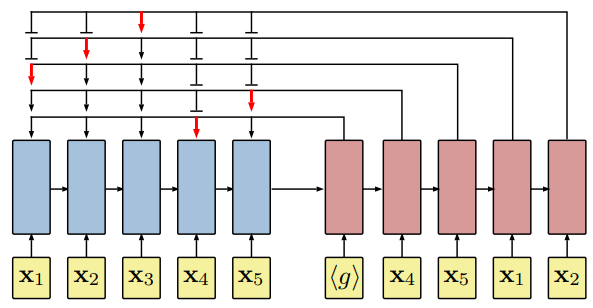
4. Optimization with Policy Gradient

Let $\theta$ be the parameters of PtrNet.

$$\begin{aligned} J(\boldsymbol{\theta} \mid s)&=\mathbb{E}_{\pi \sim p_{\theta}(. \mid s)} L(\pi \mid s) \\ J(\boldsymbol{\theta})&=\mathbb{E}_{s \sim \mathcal{S}} J(\boldsymbol{\theta} \mid s) \\ \nabla_{\theta} J(\theta \mid s)&=\mathbb{E}_{\pi \sim p_{\theta}(\cdot \mid s)}\left[(L(\pi \mid s)-b(s)) \nabla_{\theta} \log p_{\theta}(\pi \mid s)\right] \\ \nabla_{\theta} J(\theta) &\approx \frac{1}{B} \sum_{i=1}^{B}\left(L\left(\pi_{i} \mid s_{i}\right)-b\left(s_{i}\right)\right) \nabla_{\theta} \log p_{\theta}\left(\pi_{i} \mid s_{i}\right) \end{aligned}$$

where $b(s)$ is a baseline function.

Let $\theta_v$ be the parameter of critic network.

$$\mathcal{L}\left(\theta_{v}\right)=\frac{1}{B} \sum_{i=1}^{B}\left\|b_{\theta_{v}}\left(s_{i}\right)-L\left(\pi_{i} \mid s_{i}\right)\right\|_{2}^{2}$$

4.1 Search Strategies

• Sampling
  1. $s \sim S_{train}$
  2. $\{\pi_i \}\sim p_\theta(\cdot \mid s)$ for $i=1, \ldots , n_{\pi}$
  3. Evaluate $L_i = L(\pi \mid s)$
  4. $\pi^\star = \max L_i$
  5. Policy Gradient
  6. repeat 1 until convergence
  7. Greedy in test phase
• Active Search
  1. $s \sim S_{test}$
  2. Policy Gradient
  3. repeat 2 until convergence
  4. Greedy

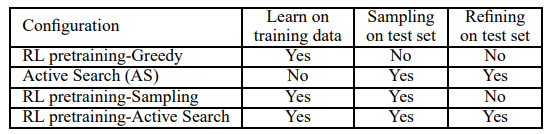
5. Experiments