Pointer Network

0. Abstract

Input Sequence의 길이에 따라 output dictionary의 사이즈가 바뀌는 경우, 해결하기 어렵다.

우리의 모델은 neural attention 메커니즘을 활용해 푼다.

이는 attention후에 섞는 대신에, 멤버들을 고르는 pointer로 사용한다.

1. Introduce

RNN encoder-decoder 구조는 input sequence와 output sequence의 길이가 다름에 적합하다.

최근, 디코더에 attention 메커니즘을 도입하였다.

이들은 NLP와 이미지, 비디오 captioning 등에 사용된다.

---

그러나 이들은 output dictionary의 size가 사전에 고정되어 있다.

그래서 combinatorial optimization problem에 적용될 수 없다.

이 논문은 attention 메커니즘을 pointer 생성하는 데 사용했다.

2. Models

2.1 Sequence-to-Sequence Model

Given a training pair $\left(\mathcal{P}, \mathcal{C}^{\mathcal{P}}\right)$,

$$p\left(\mathcal{C}^{\mathcal{P}} \mid \mathcal{P} ; \theta\right)=\prod_{i=1}^{m(\mathcal{P})} p_{\theta}\left(C_{i} \mid C_{1}, \ldots, C_{i-1}, \mathcal{P} ; \theta\right)$$

where

• $\mathcal{P}=\left\{P_{1}, \ldots, P_{n}\right\}$
• $\mathcal{C}^{\mathcal{P}}=\left\{C_{1}, \ldots, C_{m(\mathcal{P})}\right\}$

$$\theta^{*}=\underset{\theta}{\arg \max } \sum_{\mathcal{P}, \mathcal{C}^{\mathcal{P}}} \log p\left(\mathcal{C}^{\mathcal{P}} \mid \mathcal{P} ; \theta\right)$$

두개의 RNN 모델을 사용한다.

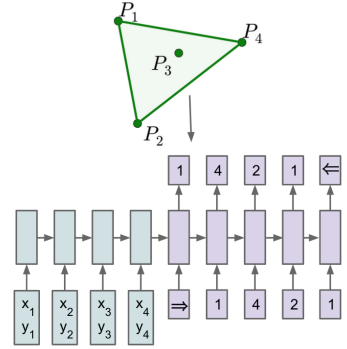
하지만 output dictionary size $n$이 매번 달라진다면, 이는 학습이 불가능해진다.

2.2 Content Based Input Attention

for i=1, ..., m(P)
	d_i = sum([a_j * e_j for j in 1:n])

각 iteration마다, $O(n)$의 계산복잡도를 가지므로, $O(n^2)$의 계산복잡도를 가진다.

하지만 input sequence의 길이가 변함에 따라 output dictionary size가 변한다면 적용이 어렵다.

2.3 Ptr-Net

$$\begin{aligned} u_{j}^{i} &=v^{T} \tanh \left(W_{1} e_{j}+W_{2} d_{i}\right) \quad j \in(1, \ldots, n) \\ p\left(C_{i} \mid C_{1}, \ldots, C_{i-1}, \mathcal{P}\right) &=\operatorname{softmax}\left(u^{i}\right) \end{aligned}$$

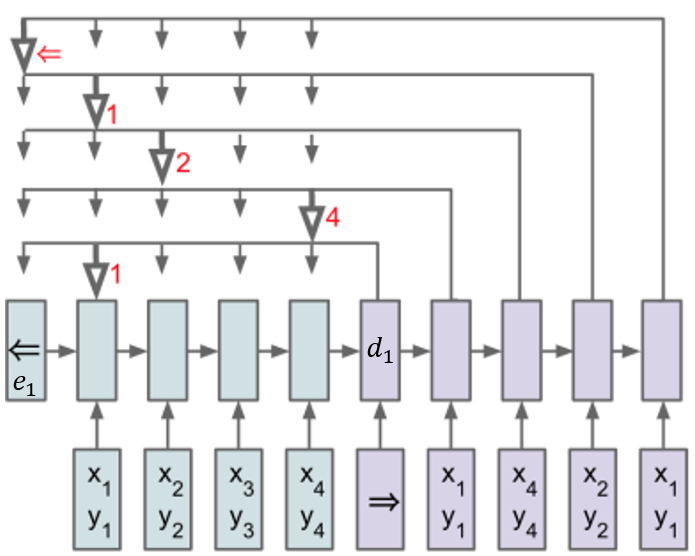
where $v, W_1, W_2$ are learnable parameters.

$O(n^2)$의 계산복잡도를 가지나, $n$의 크기에 따라 output의 크기도 변하는 구조이다.

3. Motivation and Datasets Structure

• input : $\mathcal{P}=\left\{P_{1}, \ldots, P_{n}\right\}$ where $P_{j}=\left(x_{j}, y_{j}\right) \in \left[ 0,1\right] \times \left[ 0, 1\right]$
• output : $\mathcal{C}^{\mathcal{P}}=\left\{C_{1}, \ldots, C_{m(\mathcal{P})}\right\}$

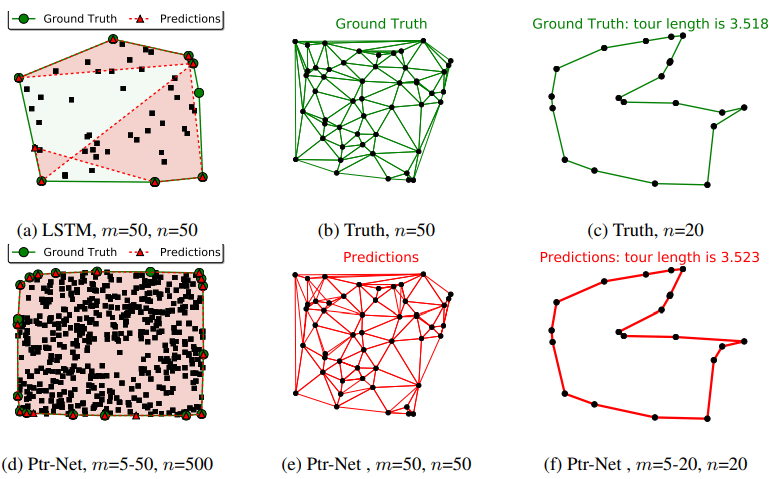
3.1 Convex Hull

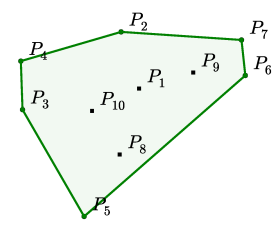
3.2 Delaunay Triangulation

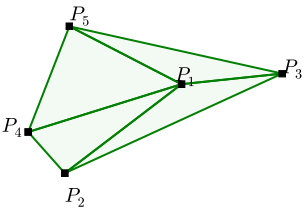
3.3 Travelling Salesman Problem (TSP)

4. Empirical Results